
- •1. Гладкая плоскость (поверхность) или опора
- •2. Гибкая нить (провода, канаты, цепи, ремни)
- •3. Невесомый стержень с шарнирами
- •5. Шарнирно-подвижная опора (опора на катках)
- •6. Жесткая заделка
- •7) Проекция силы на ось и на плоскость
- •8) Проекция силы относительно точки
- •9) Теорема Вариньона о моменте равнодействующей
- •10) Пара сил. Момент пары. Эквивалентность пар
- •11. Теорема о параллельном переносе силы
- •12. Центр параллельных сил
- •13. Координаты центров тяжести однородных тел
- •14. Законы трения скольжения
- •15 Трение качения
- •19) Естественный способ задания движения точки
- •Угловое ускорение при вращении тела
- •31) Понятие о механической системе. Силы. Геометрия масс.
- •32)Теорема о движении центра масс системы. Законы сохранения.
- •33)Количество движения точки. Импульс Силы.
- •34)Теорема об изменении количества движения точки(на всякий случай кинул и момента) и системы.
- •35)Работа силы и момента силы. Мощность
- •36) Кинетическая энергия твердых тел. В конце этого вопроса краткий вариант, постарайся и его пихнуть.
- •37)Теорема об изменении кинетической энергии точки и системы.
- •38)Осевые моменты инерции однородных тел.
- •39)Теорема о моменте инерции относительно параллельной оси.
- •40) Кинетический момент механической системы.
- •41)Дифуравнение вращательного движения твердого тела.
- •42)Сила Инерции. Динамические реакции.
-
Статика. Основные понятия и определения
Статикой называется раздел теоретической механики в котором излагается общее учение о силах и изучается равновесие материальных тел, находящихся под действием сил.
Под равновесием понимают состояние покоя тела по отношению к инерциальной системе отсчета, связанной обычно с неподвижным телом.
В качестве модели реального материального тела, в статике рассматривается абсолютно твердое тело - тело расстояние между любыми двумя точками которого всегда остается постоянным.
Совокупность сил, действующих на твердое тело, называется системой сил.
Основные понятия:
1)В статике материальные тела считают абсолютно твердыми т.к. изменение размеров тел обычно мало по сравнению с начальными размерами
2) Про тело говорят , что оно находится в равновесии, если оно покоится или движется равномерно и прямолинейно относительно выбранной инерциальной системы отсчета.
3)Тела на которые влияют внешние силы, а так же другие материальные тела ограничивающие перемещение данного тела в пространстве называют связями.
4) Сила с которой связь действует на тело ограничивая его перемещение, называется реакцией связи.
Если систему сил действующих на твердое тело можно заменить на другую систему сил, не изменяя механического состояния тела, то такие системы сил называются эквивалентными.
5,6) Для любой системы сил, приложенных к твердому телу, можно найти эквивалентную систему сил, состоящую из силы приложенной в заданной точке ( центре приведения) и пары сил, эта сила называется главным вектором системы сил, а момент создаваемый парой сил – главным моментом относительно выбранного центра приведения
-
Задачи статики. Аксиомы статики.
Две основные задачи статики.
1. Задача о приведении системы сил: заключается в замене данной системы сил другой, наиболее простой, ей эквивалентной.
2. Задача о равновесии состоит в определении условий, при которых система сил приложенная к телу будет уравновешенной системой.
Аксиомы:
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находится в равновесии только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны: (Силы указаны векторно)
F1 = - F2.
Система сил F1 и F2 называется уравновешивающейся, или эквивалентной нулю: F1+ F2 = 0.
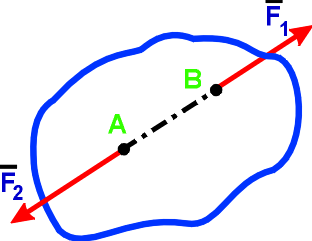
Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней добавить или от нее отнять уравновешенную систему сил.

Аксиома 3. Две силы, приложенные к телу в одной точке, можно заменить одной, приложенной в той же точке, которая является диагональю параллелограмма, построенного на этих силах как на сторонах:
R = F1+ F2 .
Сила R, которая эквивалентна данной системе сил F1и F2 называется равнодействующей. Ее модуль вычисляется по формуле
|
R = [F12+ F22 + 2F1F2cosa]1/2 |
где a- угол между силами F1 и F2 .
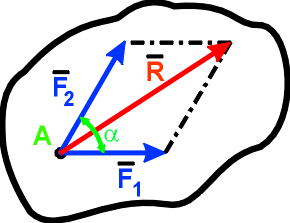
Аксиома 4. Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны:
FA = - FB.
Cилы FA и FB не образуют уравновешенную систему сил, так как они приложены к разным телам.

Аксиома 5. Равновесие деформируемого тела не нарушится, если тело считать отвердевшим (абсолютно твердым)
-
Связи и их реакции.
Связи и их реакции
Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.
Тело, перемещениям которого препятствуют какие-нибудь другие,скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.
Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.
Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей.
Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций.
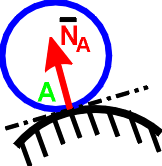
1. Гладкая плоскость (поверхность) или опора
Реакция N гладкой
плоскости (поверхности) или опоры
направлена по общей нормали к поверхностям
соприкасающихся тел в точке их касания
и приложена к этой точке.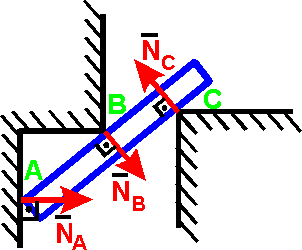
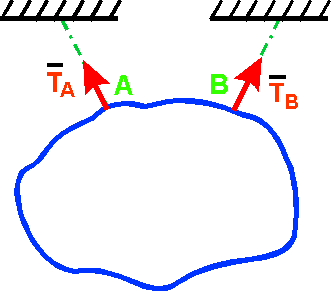
2. Гибкая нить (провода, канаты, цепи, ремни)
Реакция Т направлена вдоль нити к точке подвеса.
3. Невесомый стержень с шарнирами
Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция Nизображается от тела по стержню, в предположении, что в равновесии стержень растянут.
4. Неподвижный цилиндрический шарнир или подшипник
Реакция RA цилиндрического
шарнира может иметь любое направление
в плоскости, перпендикулярной оси
вращения, т. е. в плоскости Аху.
Обычно ее раскладывают на две
составляющие ХА и YA по
двум взаимноперпендикулярным направлениям.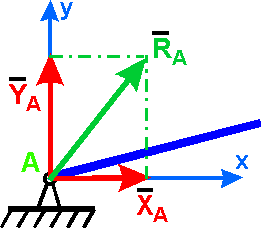
5. Шарнирно-подвижная опора (опора на катках)
Реакция R проходит
через ось шарнира и направлена
перпендикулярно к опорной плоскости.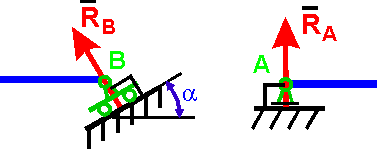
6. Жесткая заделка
Нахождение
реакции жесткой заделки сводится к
определению составляющих ХА и YA препятствующих
линейному перемещению балки в плоскости
действия сил, и алгебраической величине
момента mA,
препятствующего вращению балки под
действием приложенных к ней сил.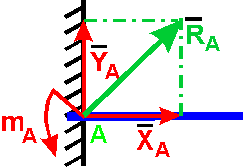
4. Система сходящихся сил на плоскости. Равнодействуящая сил. Разложение сил
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.
Точка пересечения линий действия сил называется точкой сходимости.
Действие системы сходящихся сил F1, F2, ..., Fn на тело эквивалентно действию одной силы R, которая называется равнодействующей:
R = F1 + F2 + ... + Fn = ∑Fk. (k = 1, 2, .., n)

Равнодействующая R приложена в точке сходимости О и является замыкающим вектором при построении силового многоугольника.
Для равновесия твердого
тела, находящегося под действием сходящейся
системы сил,
необходимо и достаточно,
чтобы равнодействующая этих
сил была равна
нулю: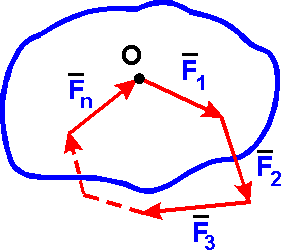
R = 0,
или
|
F1 + F2 + ... + Fn = 0. |
Геометрическим условием равновесия твердого тела, находящегося под действием сходящейся системы сил F1 + F2 + ... + Fn является замкнутостьсилового многоугольника, т. е. начало первого вектора F1 должно совпадать с концом последнего Fn.
Аналитические условия равновесия. При равновесии системы сил модуль равнодействующей R = [Rх2 + Rу2]1/2 = 0, поэтому Rх = ∑Fkх = 0, Rу = ∑Fky = 0.
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на оси прямоугольной системы координат Оху были равны нулю:
|
∑Fkх = 0, ∑Fky = 0. (k = 1, 2, ..., n) |
Эти два условия называются аналитическими условиями равновесия для плоской системы сходящихся сил.
Теорема
о трех не непараллельных силах: если
твердое тело находится
в равновесии под
действием трех непараллельных сил,
лежащих в одной плоскости, то линии
действия этих
сил пересекаются
в одной точке.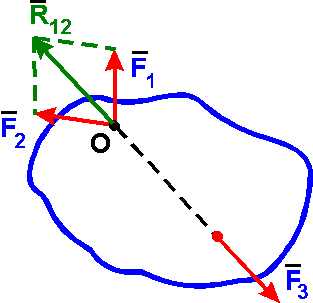
Так как F1 + F2 + F3 = 0, то F1 + F2 = R12 = - F3. Cледовательно, согласно аксиоме 1 линия действия силы F3 пересекает точку О - сходимости сил F1 и F2.
5.Геометрические и аналитические уравнения равновесия системы сил.
Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).
Отсюда вытекает условие равновесия произвольной пространственной системы сил.
В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю
R = 0, Mo = 0.
В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю
ΣFkx = 0, ΣFky = 0, ΣFkz = 0,
Mx(Fk) = 0, My(Fk) = 0, Mz(Fk) = 0.
Условия равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин (реакций связей).
Чтобы задача была статически определимой, число неизвестных должно быть не более шести.
В частности, для системы параллельных сил условиями равновесия являются следующие равенства
ΣFkx = 0, Mx(Fk) = 0, My(Fk) = 0.
6)
