3.4.7 Ланка запізнення

1. Рівняння ланки:

де t - час запізнювання, є трансцендентним.

В операторній формі при нульових початкових умовах це рівняння має вигляд

2. Передаточна функція:

3. Частотні характеристики: Частотна передаточна функція:

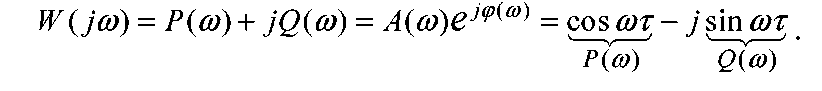
Звідки

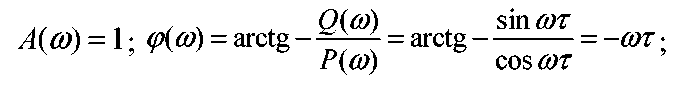
На рис. 3.17 подані відповідні графіки.

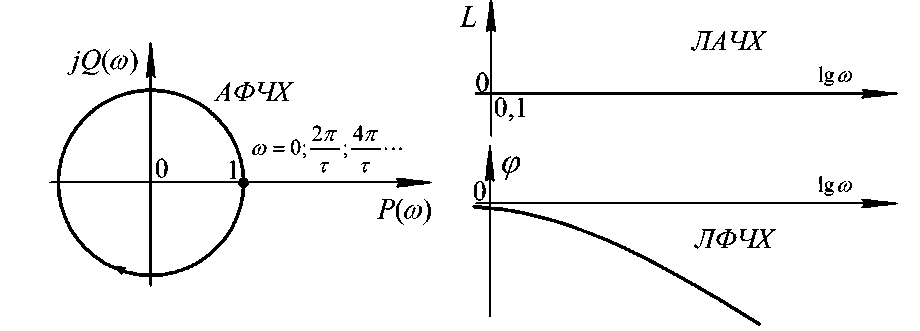
Рис. 3.17 – Частотні характеристики

Таким чином, співвідношення амплітуд вхідного і вихідного сигналів не залежить від частоти, а відставання за фазою вихідного сигналу тим більше, чим більше частота.

4. Часові характеристики:

- перехідна характеристика

- імпульсна перехідна характеристика

Вигляд цих характеристик представлений на рис. 3.18.

Рис. 3.18 – Часові характеристики

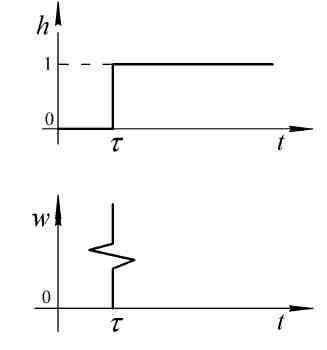
Слід зазначити, що ланка запізнення в більшості випадків погіршує стійкість системи, в яку входить, і робить її важко керованою. Крім того, аналіз і синтез таких систем пов'язаний з більшими труднощами.

У практичних розрахунках передаточну функцію ланки апізнення W(s) звичайно приблизно заміняють дрібно-раціональними функціями:

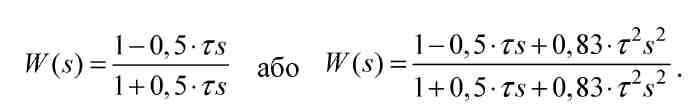
На закінчення роздягнула введемо нове поняття – мінімально-фазова ланка. Під такою ланкою матимемо на увазі ланку, в якій при одній і тій же частоті зміщення фази за модулем менше, ніж у будь-якої іншої ланки, що має однакову з нею АЧХ.

3.5 Стійкість САК

Під стійкістю системи розуміється здатність її повертатися до стану сталої рівноваги після зняття збурювання, що порушило цю рівновагу. Нестійка система безупинно віддаляється від рівноважного стану або робить довкола нього коливання зі зростаючою амплітудою.

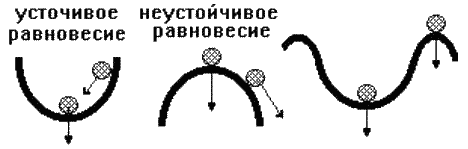
Рис. 3.19

Стійкість лінійної системи визначається не характером збурювання, а структурою самої системи (рис. 3.19). Говорять, що система стійка "у малому", якщо визначено факт наявності стійкості, але не визначені її границі. Система стійка "у великому", коли визначені границі стійкості й те, що реальні відхилення не виходять за ці границі.

В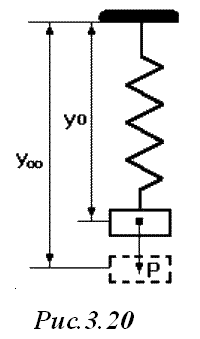ідповідно до класичного методу рішення диференціального рівняння шукається у вигляді:

 y(t) = y_вын(t) + y_св(t).

Тут yсв(t) - загальне рішення однорідного диференціального рівняння, тобто рівняння з нульовою правою частиною:

  a_oy⁽ⁿ⁾ + a₁y^(n-1) + ... + a_(n-1)y’ + a_(n)y = 0.

 Фізично це означає, що всі зовнішні впливи зняті й система абсолютно вільна, її рухи визначаються лише власною структурою. Тому рішення даного рівняння називається вільної складової загального рішення. y_вын(t) - частка рішення неоднорідного диференціального рівняння, під яким розуміється рівняння з ненульовою правою частиною. Фізично це означає, що до системи прикладений зовнішній вплив u(t). Тому друга складова загального рішення називається змушений. Вона визначає змушений сталий режим роботи системи після закінчення перехідного процесу.

Можна провести аналогію між САК й пружиною, коливання якої описуються аналогічним диференціальним рівнянням рис. 3.20, 3.21. Відтягнемо пружину, а потім відпустимо, надавши її самої собі. Пружина буде коливатися у відповідності з вільної складового рішення рівняння, тобто характер коливань буде визначатися тільки структурою самої пружини.

Якщо в момент часу t = 0 підвісити до пружини вантаж, то на вільні коливання накладеться зовнішня сила Р. Після загасання коливань, описуваних тільки вільного складового загального рішення, система перейде в новий сталий режим, характеризуємий змушеної складової y_вын = y(t ). Якщо зовнішній вплив саме буде змінюватися за синусоїдальним законом P=P_osin( t+ ), то після загасання перехідного процесу система буде робити змушені коливання з тією же частотою, що й сила, що змушує, тобто y_вын = y_maxsin( t + y).

Кожна складова загального рішення рівняння динаміки шукається окремо. Змушена складова шукається на основі рішення рівняння статики для даної системи для часу t . Вільна складова являє собою суму з n окремих скдадових

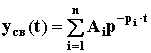
де p_i корінь характеристичного рівняння D(p) = a₀p_n + a₁p_n-1 + a₂p_n-2 + ... + a_n = 0. Коріння можуть бути або речовинними p_i = a_i, або попарно комплексно сполученими p_i = a_i ± j i. Постійні інтегрування А_i визначаються виходячи з початкових і кінцевих умов, підставляючи в загальне рішення значення u, y й їхні похідні в моменти часу t = 0 й t .

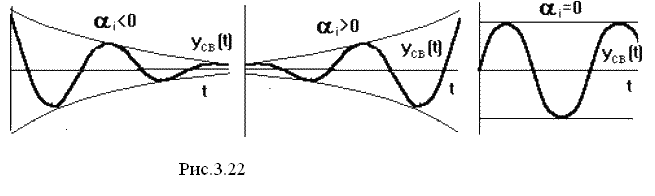
Кожному негативному речовинному кореню відповідає експоненціиально загасаюча в часі складова y_св(t)_i, кожному позитивному - експоненціиально розбіжному, кожному нульовому кореню відповідає y_св(t)_i = const (рис. ). Пари комплексно сполучених корінь із негативною речовинною частиною визначає загасаючі коливання із частотою _i, при позитивній речовинній частині - розбіжні коливання, при нульовий - незатухаючі рис. 3.22.

Тому що після зняття збурювання y_вын(t) = 0, то стійкість системи визначається тільки характером вільної складової y_св(t). Тому умова стійкості систем по Ляпунову формулюється так: у стійкій системі вільна складова р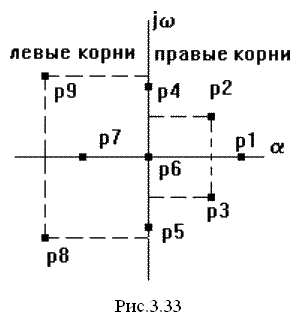ішення рівняння динаміки, записаному у відхиленнях, повинна прагнути до нуля, тобто загасати.

Виходячи з розташування на комплексній площині корінь із негативними речовинними частинами називаються лівими, з позитивними - правими рис. 3.33. Тому умова стійкості лінійної САК можна сформулювати в такий спосіб: для того, щоб система була стійка, необхідно й досить, щоб всіх корінь її характеристичного рівняння були лівими. Якщо хоча б один корінь правий, то система нестійка. Якщо одне з корінь дорівнює нулю (у системах, де a_n = 0), а інша ліві, то система перебуває на границі аперіодичної стійкості. Якщо дорівнюють нулю речовинні частини однієї або декількох пар комплексно сполучених корінь, то система перебуває на границі коливальної стійкості.

Правила, що дозволяють судити про знаки корінь характеристичного рівняння без його рішення, називаються критеріями стійкості. Їх можна розділити на алгебраїчні (засновані на складанні по даному характеристичному рівнянню за певними правилами алгебраїчних виражень, по яких можна судити про стійкість САК) і частотні (засновані на дослідженні частотних характеристик).

Критерій Гурвица

 Гурвиц запропонував інший критерій стійкості. З коефіцієнтів характеристичного рівняння будується визначник Гурвица по алгоритму:

1) по головній діагоналі ліворуч праворуч виставляються всі коефіцієнти характеристичного рівняння від a₁ до a_n;

2) від кожного елемента діагоналі нагору й униз добудовуються стовпці визначника так, щоб індекси убували зверху вниз;

3) на місце коефіцієнтів з індексами менше нуля або більше n ставляться нулі.

Критерій Гурвица: для того, щоб САК була стійка, необхідно й досить, щоб всі n діагональних мінорів визначника Гурвица були позитивні. Ці мінори називаються визначниками Гурвица.

Розглянемо приклади застосування критерію Гурвица:

1) n = 1 => рівняння динаміки: a₀p + a₁ = 0. Визначник Гурвица: = ₁ = a₁ > 0 при a₀ > 0, тобто умова стійкості: a₀ > 0, a₁ > 0;

2) n = 2 => рівняння динаміки: a₀p² + a₁p + a₂ = 0. Визначники Гурвица: ₁ = a₁ > 0, D₂ = a₁a₂ - a₀a₃ = a₁a₂ > 0, тому що a₃ = 0, тобто умова стійкості: a₀ > 0, a₁ > 0, a₂ > 0;

3) n = 3 => рівняння динаміки: a₀p³ + a₁p² + a₂p + a₃ = 0. Визначники Гурвица: ₁ = a₁ > 0, ₂ = a₁a₂ - a₀a₃ > 0, 3 = a_{3 2} > 0, умова стійкості: a₀ > 0, a₁ > 0, a₂ > 0, a₃ > 0, a₁a₂ - a₀a₃ > 0;

У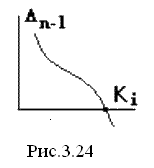 такий спосіб при n 2 позитивність коефіцієнтів характеристичного  рівняння є необхідною й достатньою умовою стійкості САК. При n > 2 з'являються додаткові умови.

Критерій Гурвица застосовують при n 4. При більших порядках зростає число визначників і процес стає трудомістким. Є ряд модифікацій даного критерію, що розширюють його можливості.

Недолік критерію Гурвица - мала наочність. Достоїнство - зручний для реалізації на ЕОМ. Його часто використають  для  визначення  впливу одного з параметрів САУ на її стійкість. Так рівність нулю головного визначника _n = a_{n n-1} = 0 говорить про те, що система перебуває на границі стійкості. При цьому або a_n = 0 - при виконанні інших умов система перебуває на границі аперіодичної стійкості, або передостанній мінор _n-1 = 0 - при позитивності всіх інших мінорів система перебуває на границі коливальної стійкості. Параметри САУ визначають значення коефіцієнтів рівняння динаміки, отже, зміна будь-якого параметра Ki впливає на значення визначника _n-1. Досліджуючи цей вплив можна знайти, при якому значенні Ki визначник _n-1 стане дорівнює нулю, а потім - негативним рис. . Це й буде граничне значення досліджуваного параметра, після якого система стає нестійкою.