21.1.1.2.1. Простейшая модель атома в поле световой волны

Под действием световой волны совершают колебания только внешние электроны атома, их называют оптическими электронами. Будем считать, что у молекулы (атома) - один оптический электрон. Моделью такого атома будет упругий диполь, дипольный момент которого (см. 9.13.1.1):

.

Оптический электрон будет двигаться под действием квазиупругой силы, силы "трения" и внешней силы, действующей со стороны электрического поля световой волны. Если световая волна поляризованная, то все эти силы будут действовать вдоль одной прямой. Направим вдоль этой прямой ось x, начало координат совместим с положительным зарядом, который будем, в первом приближении, считать неподвижным. Таким образом, мы приходим к модели пружинного маятника, который совершает колебания под действием внешней гармонической силы.

21.1.1.2.2. Уравнение движения электрона и его решение

Уравнение движения, описывающее вынужденные колебания маятника с затуханием было получено нами из второго закона Ньютона в разделе 14.5.5.:

.

Здесь у нас x - координата электрона, ω₀ - собственная частота незатухающих колебаний электрона, β - коэффициент затухания, а

.

E_m - амплитуда световой волны;

ω - циклическая частота световой волны; m_e- масса электрона, e - элементарный заряд (e = 1,6 10-19 Кл).

Стационарное решение этого уравнения движения (14.5.6.1):

,

где

21.1.1.2.3. Проекции дипольного момента и напряженности поля волны на ось X

На следующем рисунке изображен диполь, силы действующие на его полюсы, ось x и вектор электрического поля волны в момент времени t = 0:

Как видно из рисунка, проекция дипольного момента (21.1.1.2.1) на ось x:

.

Проекция напряженности электрического поля световой волны на ось x:

,

знак минус означает, что в начальный момент времени вектор направлен против оси x. Напомним, что в нашем уравнении движения (21.1.1.2.2) сила, действующая на электрон, при t = 0 имеет положительный знак.

21.1.1.3. Выражение для n2

Подставим в формулу, полученную в (21.1.1.2) для n², выражения p_x(t), N_x(t) с использованием для x(t) решения уравнения движения, записанное в (21.1.1.2.2):

При усреднении по времени дает . Подставляя выражение для амплитуды A-колебаний электрона (из 21.1.1.2.1) получим:

;

.

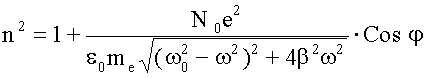21.1.1.4. Анализ зависимости n(ω)

Как показывает опыт затухание оказывает незначительное влияние на движение оптического электрона, если частота световой волны не равна ω₀ - собственной частоте колебаний электрона. Точнее, затуханием можно пренебречь, если

.

При выполнении этого условия

.

В первом случае (если ω < ω₀) колебания электрона происходят в фазе с вынуждающей силой, Cosφ = 1. Во втором (ω > ω₀) - в противофазе, Cosφ = -1.

Учитывая это можно записать упрощенное выражение для n², применимое для частот далеких от ω₀:

.

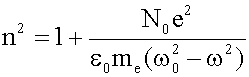Здесь знак второго слагаемого при ω < ω₀ положителен, при ω > ω₀ второе слагаемое отрицательное.

Для ω = ω₀ φ = π/2, а Cosφ = 0, тогда, возвращаясь к исходному выражению для n² (20.1.1.3), получим:

n = 1.

 

21.1.1.5. График зависимости n(ω)

Проведенный анализ позволяет изобразить примерный вид графика зависимости показателя преломления от циклической частоты:

На участках AB и DE n растет с ростом ω - дисперсия нормальная. На участке BCD дисперсия аномальная - с ростом показатель преломления падает.

21.1.1.2.6. График зависимости n(λ)

Так как длина волны λ и циклическая частота величины, связанные обратно пропорциональной зависимостью (15.1.8), то график n(λ), соответствующий приведенному выше графику, будет иметь примерно следующий вид:

.

21.1.1.2.7. Учет колебаний с другими собственными частотами

В веществе могут быть заряды, колеблющиеся с различными собственными частотами ω₀ и затуханиями β_i, величины зарядов q_i могут быть разными, разными могут быть и их массы. С учетом этого формула для n² примет следующий вид:

.

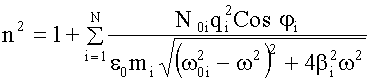График зависимости n(ω) при наличии двух собственных частот (N = 2) будет иметь следующий вид:

Опыт подтверждает такой ход зависимости n(ω).

21.2. Групповая скорость

На графике зависимости n(λ), изображенном в 21.1.1, есть участок CDE, где n < 1. Это означает, что фазовая скорость световой волны:

на участке CDE.

На первый взгляд это утверждение противоречит теории относительности (см. раздел 8), согласно которой скорость света в вакууме является максимально возможной скоростью передачи сигнала. Но монохроматическая волна не может передавать сигнал: она никогда не кончается и нигде не начинается. Такая волна состоит из бесконечно повторяющихся одинаковых горбов и впадин, ничем не отличающихся друг от друга. Передавать сигнал можно только ограниченным в пространстве и во времени кусочком электромагнитной волны - электромагнитным импульсом. Такой импульс (группа волн) можно представить в виде наложения бесконечного числа монохроматических волн с разными частотами и амплитудами (интеграл Фурье).

Мы, для простоты будем представлять импульс (группу волн) совокупностью двух близких по частоте монохроматических волн:

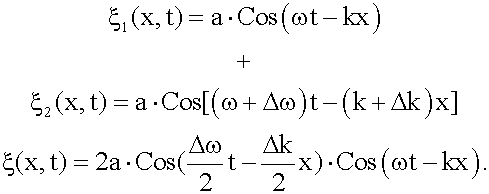
Здесь мы во втором сомножителе пренебрегаем величинами Δω и Δk по сравнению с ω и k.

Выражение стоящее в квадратных скобках медленно меняется в пространстве и во времени, т. к. Δω << ω, Δk << k (сравните с 14.3.3). Обозначим его буквой A,

.

Тогда можно считать, что наш импульс (группа волн) - это монохроматическая волна с медленно меняющейся амплитудой:

.

Будем следить за распространением в пространстве точки x_m, где амплитуда A максимальна. Назовем групповой скоростью u скорость перемещения в пространстве точки с координатой x_m:

.

Максимуму A соответствует обращение в ноль фазы косинуса в выражении для A, т.е.

.

Возьмем производную по времени от этого выражения, в результате получим:

,

откуда

.

Переходя к пределу, получим окончательное выражение для групповой скорости:

.