43. Условный экстремум

1) Усл-ый экстремум (метод множ-ей Лагранжа):

Постановка задачи: Найти экстремумы ф-ии Z=f(x,y) при усл, что φ(x,y)=0. Составляют ф-ию Лагранжа:

L=f(x,y) + η φ(x,y) ; η – множ-ль Лагранжа.

Для того, чтобы найти т экстремума, находят стац-е точки ф-ии Лагранжа, т.е. решают систему:

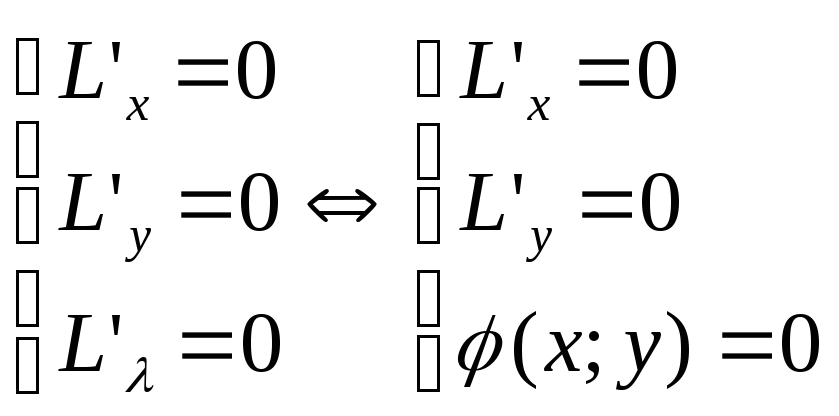
Достат-ое усл экстремума: Если опред-ль ∆>0, то экстр-м есть и при том max; Если ∆<0 => экст-м есть – min

вычисленный в точке (x₀, y₀, λ ₀) (стац т).

44. Метод наименьших квадратов.

(x₁; y₁)

(x₂; y₂)

(x_n; y_n)

Подобрать теоретич. прямую вида y=ax+b "наилучшим образом" согласующуюся с этими данными.

δi=y_{i теор} – y_{i эмпирич}; МНК:∑(δi)²→min

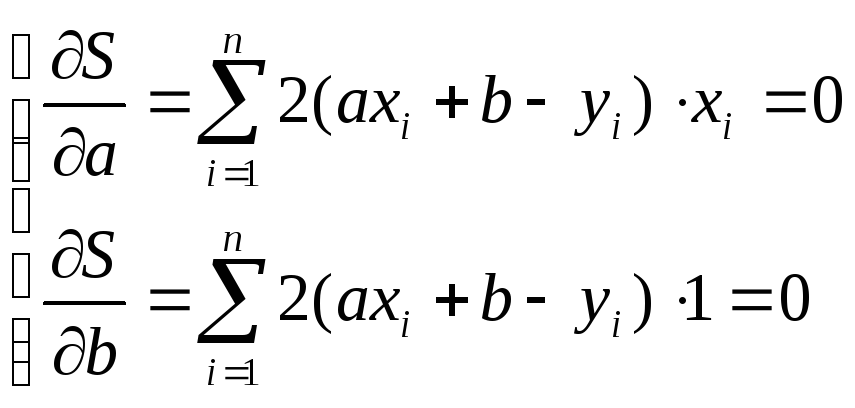
45. Первообразная

Функция F(x)называется первообразной для функции f(x) на промежутке X если для любого x  X функция F(x) дифференцируема и выполняется равенство F’(x)=f(x)

Пример. Для функции f(x)=cosx первоообразной будет F(x)=Sinx на промежутке от (-бесконечность до +бесконечность) итд

Вообщем просто по таблице производных в обратную сторону НО смотрите на промежуток, так как например F(x)=lnx это первообразная для f(x)=1/x на промежутке (0;+бесконечность) то есть надо смотреть на промежутки так как не все они будут существовать В последнем примере от нуля до бесконечности потому что Х в знаменателе если кто не понял