1.1.4. Центр параллельных сил и центр тяжести

1. Теорема о сложении двух параллельных сил, направленных в одну сторону

Равнодействующая двух параллельных сил, направленных в одну сторону, равна арифметической сумме этих сил, параллельна им и направлена в ту же сторону, а линия действия равнодействующей делит прямую АВ на части обратно пропорциональные этим силам.

2. Теорема о сложении двух параллельных сил, направленных в противоположные стороны

Равнодействующая двух параллельных сил, направленных в одну сторону, равна разности этих сил, параллельна им и направлена в сторону большей по модулю силы, а линия действия равнодействующей делит продолжение прямой АВ со стороны большей силы на части обратно пропорциональные этим силам.

Точка С –центр параллельных сил –это точка, через которую проходит линия действия равнодействующей системы параллельных сил.

3. Центр параллельных сил. Центр тяжести тела

Любое тело можно представить как совокупность точек С –центров параллельных сил, каждая из которых обладает силой тяжести. Эти силы направлены по радиусу к центру Земли. Поскольку размеры тел, с которыми приходится иметь дело в механике, ничтожно малы по сравнению с радиусом Земли, то считают, что все эти силы тяжести параллельны между собой и направлены в одну сторону.

Равнодействующая этих сил тяжести называется весом тела.

Точка С –центр параллельных сил зависит от точек приложения сил F₁ и F₂ и от величины этих сил.

Центром тяжести тела называют точку, через которую проходит вес тела.

4. Координаты центра параллельных сил

Теорема Вариньона:

Момент равнодействующей плоской системы сил относительно произвольно взятой точки равен алгебраической сумме моментов составляющих сил относительно той же точки.

Формулы для определения координат центра параллельных сил:

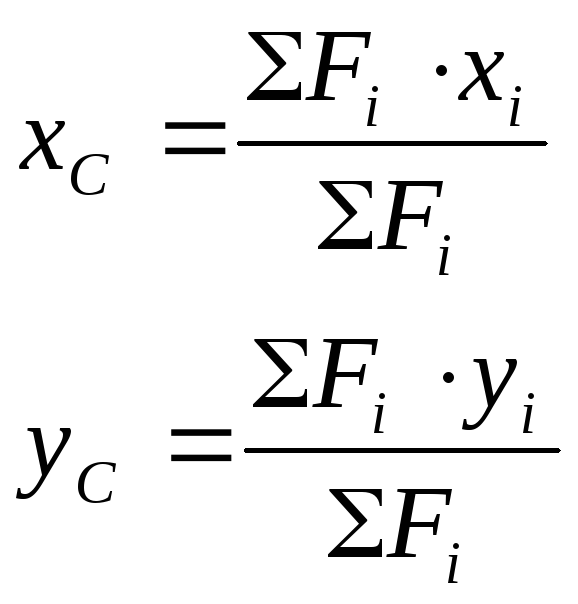
5. Координаты центра тяжести площадей

В инженерных расчётах часто требуется определить центр тяжести плоской фигуры весом Р. Эта сила равномерно распределена по всей площади пластинки, так что G=А∙γ, где γ –сила тяжести, приходящаяся на единицу площади (вес 1м² площади).

Сила тяжести каждого участка:

G_i=A_i∙γ_i

A_i –площадь i-того участка.

Формулы координат центра тяжести площадей

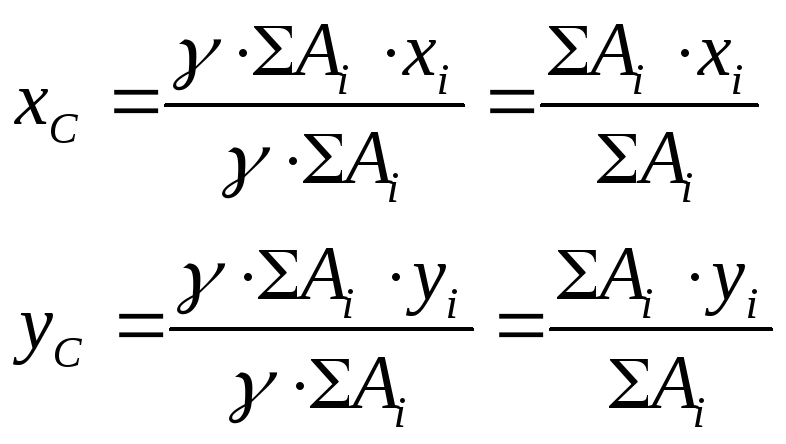
6. Центры тяжести простых фигур

Прямоугольник С –точка пересечения диагоналей	Треугольник С –точка пересечения медиан
Дуга окружности	Круговой сектор При α=π/2 (полукруг)

7. Алгоритм решения задач по методу разбиения

1. Разбиваем сечение на простейшие фигуры.

2. Показываем на чертеже центры тяжести каждой фигуры.

3. Выбираем оси отсчёта, если они не указаны.

4. Указываем на чертеже координаты центра тяжести каждой простейшей фигуры относительно осей отсчёта.

5. Находим площади и координаты центров тяжестей всех простейших фигур в отдельности.

6. Определяем координаты центра тяжести всей составной фигуры и показываем на чертеже точку С и её координаты.