Ограниченные и неограниченные последовательности
Числовая последовательность {хn} называется ограниченной, если существуют числа m и M, такие, что любой элемент xn этой последовательности удовлетворяет неравенствам
m ≤ xn ≤ M.
Пусть
А
= max{ | m
|, | M |}.
Тогда условие ограниченности
последовательности можно записать в
виде | xn
| ≤ А
n
≥ N:
Здесь
и в дальнейшем будем пользоваться
квантором всеобщности
и
квантором существования
.
Не вдаваясь в подробности определения
этих логических операций, будем читать
квантором всеобщности
как
"для любого", а квантор существования
как
"существует". Последовательность
{хn}
называется неограниченной, если для
любого как угодно большого положительного
числа А существует элемент xn
этой последовательности, удовлетворяющий
неравенству | xn
| > A, (т.е. либо xn
> A, либо xn
< - A):
Последовательность ограничена сверху, если все ее элементы принадлежат промежутку ( - ∞, M]:
Последовательность ограничена снизу, если все ее элементы принадлежат промежутку [m, + ∞):
З
а м е ч а н и е.
Неограниченная последовательность
может быть ограничена сверху
(снизу).
Сравнивая запись с
помощью логических символов двух
последних определений, видим, что при
построении отрицаний символы
и
заменяют
друг друга и неравенства меняют свой
смысл.
25) Бесконечно большие и бесконечно малые последовательности
Определение. Последовательность { хn} называется бесконечно большой, если для как угодно большого любого положительного числа А существует номер N, зависящий от этого числа А, такой, что для всех последующих номеров n > N выполняется неравенство | xn | > A:
Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n + 1, … не является бесконечно большой, поскольку при A > 1 неравенство | xn| > A выполняется не для всех элементов xn с нечетными номерами. Определение. Последовательность {αn} называется бесконечно малой, если для любого как угодно малого положительного числа ε > 0 существует номер N, зависящий от этого ε, такой, что для любых n > N выполняется неравенство |αn| < ε:
Свойства бесконечно малых и бесконечно больших величин и связь между ними
Пусть
f1
(x)
и f
2
(x)
бесконечно малые величины при
,
т.е.
и
.
1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:
.
(4.17)
2. Произведение бесконечно малых величин есть величина бесконечно малая:
.
(4.18)
3.
Произведение бесконечно малой величины
на константу С
или на функцию, имеющую конечный предел
,
есть величина бесконечно малая:
.
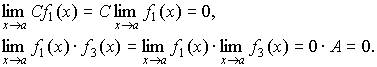Пусть
и
бесконечно
большие величины при
,
т.е.
и
.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
.
2. Произведение бесконечно больших величин есть величина бесконечно большая:
.
3.
Произведение бесконечно большой величины
на константу С,
или на функцию, имеющую конечный предел
,
есть величина бесконечно большая:
26) Теорема о двух милиционерах — теорема в математическом анализе о существовании предела у функции, которая «зажата» между двумя другими функциями, имеющими одинаковый предел. Формулируется следующим образом:
|
Если
функция y
= f(x)
такая, что
Равномерная сходимость. Отличие равномерной сходимости от поточечной в том, что скорость сходимости не зависит от точки. Определение. Последовательность функций fn : X ! R равномерно сходится на X к функции f, если 8" > 0 9N = N(") 8x 2 X (n > N ) jfn(x) f(x)j < "): Равномерная сходимость обозначается через fn(x) f(x). Природа множества X здесь никакой роли не играет. Можно считать, что X Rk. Дальше потребуется, чтобы X было компактно и измеримо (по Жордану). При необходимости уменьшить затрудняющий продвижение дискомфорт, первоначально полезно думать, что X является просто отрезком числовой оси. Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии не более чем заданное. Определение Последовательность
точек
|
для
всех x
в некоторой окрестности точки a,
причем функции φ(x)
и ψ(x)
имеют одинаковый предел при
,
то существует предел функции y
= f(x)
при
,
равный этому же значению, то есть
метрического
пространства
(X,ρ)
называется фундаментальной,
если она удовлетворяет критерию
Коши:
существует
такое натуральное
Nε,
что
для
всех n,m
> Nε.27) Функция f (отображение, операция, оператор) — это закон или правило, согласно которому каждому[3] элементу x из множества X ставится в соответствие единственный элемент y из множества Y.[4]
При этом говорят, что функция f задана на множестве X, или что f отображает X в Y.
Если
элементу
сопоставлен
элемент
,
то говорят, что элемент y
находится в функциональной
зависимости
f
от элемента x.
При этом переменная x
называется аргументом
функции f
или независимой
переменной,
множество X
называется областью
задания
или областью
определения
функции, а элемент y,
соответствующий конкретному элементу
x —
частным
значением
функции f
в точке x.
Множество Y
всех возможных частных значений функции
f
называется её областью
значений
или областью
изменения
Число
A
называется пределом
функции 
при 
,
если для любого произвольно малого
числа ε > 0 существует такое
число δ(ε), что для всех x,
удовлетворяющих условию
|
|
|
(11) |
|
выполняется неравенство
|
|
|
(12) |
|
Для
обозначения предела функции 
при 
используется символическое выражение
или запись вида
.Равномерная
сходимость
последовательности
функций
(отображений)
— свойство последовательности
,
где X
— произвольное множество,
Y
= (Y,d)
— метрическое
пространство,
сходится
к функции (отображению)
,
означающее, что для любого
существует
такой номер Nε,
что для всех номеров n
> Nε
и всех точек
выполняется
неравенство
Обычно
обозначается
.
Это условие равносильно тому, что
28) Первый замечательный предел:
