5) Определение

Пусть и , где , — два конечных множества.

Назовём матрицей размера (читается m на n) с элементами из некоторого кольца или поля отображение вида

.

Если индекс i пробегает множество M, а j пробегает множество N, то элемент A(i,j) оказывается элементом матрицы, находящемся на пересечении i-той строки и j-ого столбца:

• i-ая строка матрицы состоит из элементов вида A(i,j), где j пробегает всё множество N;

• j-ый столбец матрицы состоит из элементов вида A(i,j), где i пробегает всё множество M.

Таким образом, матрица размера состоит в точности из

• m строк (по n элементов в каждом)

• и n столбцов (по m элементов в каждом).

В соответствии с этим

• каждую строку матрицы можно интерпретировать как вектор в n-мерном координатном пространстве ;

• каждый столбец матрицы — как вектор в m-мерном координатном пространстве .

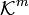Сама матрица естественным образом интерпретируется как вектор в пространстве имеющим размерность mn. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); то что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.

Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m = n называется размером квадратной матрицы или её порядком.

Линейные операции над матрицами.

 1.        Сложение матриц.

 

Определение 3.4. Суммой матриц А и В одинаковой размерности mn называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:

Свойства сложения:1 А + В = В + А. 2   (А + В) + С = А + (В + С) . 3.  Если О – нулевая матрица, то А + О = О + А = А

ЗаЗамечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.

 Пример.

 2.        Умножение матрицы на число.

 Определение 3.5. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

Свойства умножения матрицы на число:

1.        (km)A=k(mA).

2.        k(A + B) = kA + kB.

3.        (k + m)A = kA + mA.

 Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е. С = А + (-1)В.

 Пример.

. Тогда

6) Умножение матриц это наиболее важная операция, которая постоянно используется в трехмерной компьютерной графике. Именно умножение матриц позволяет осуществлять преобразование векторов и комбинировать несколько преобразований в одно. Преобразования будут рассмотрены в следующем разделе.

Чтобы получить произведение матриц AB необходимо чтобы количество столбцов матрицы A было равно количеству строк матрицы B. Если условие выполняется, произведение матриц определено. Рассмотрим представленные ниже матрицы A и B, с размерностью 2 × 3 и 3 × 3 соответственно:

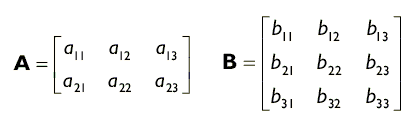
Как видите, произведение AB определено поскольку количество столбцов матрицы A равно количеству строк матрицы B. Обратите внимание, что произведение BA, получаемое в результате перестановки множителей, не определено, потому что количество столбцов матрицы B не равно количеству строк матрицы A. Это говорит о том, что в обшем случае операция умножения матриц не коммутативна (то есть AB ≠ BA). Мы говорим «в общем случае не коммутативна» по той причине, что существует ряд частных случаев в которых операция умножения матриц ведет себя как коммутативная.

После того, как мы узнали в каких случаях произведение матриц определено, можно дать определение операции умножения матриц: если A — это матрица m × n, а B — матрица n × p, то их произведением будет матрица C, размером m × p, в которой элемент c_ij находится как скалярное произведение i-го вектора-строки матрицы A и j-го вектора-столбца матрицы B:

В этой формуле a_i обозначает i-ый вектор-строку в матрице A, а b_j — j-ый вектор-столбец матрицы B.

Давайте для примера вычислим произведение:

Произведение определено, поскольку количество столбцов матрицы A равно количеству строк матрицы B. Кроме того, обратите внимание, что размер полученной в результате матрицы — 2 × 2. Согласно формуле (4) получаем:

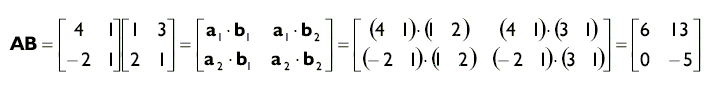
В качестве упражнения проверьте, что в данном случае AB ≠ BA.

И еще один, более общий, пример: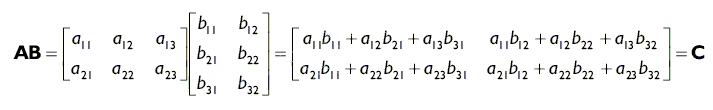

7) Рассмотрим квадратную матрицу

 .

Обозначим  =det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если  = 0.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через А^1, так что В = А^1. Обратная матрица вычисляется по формуле

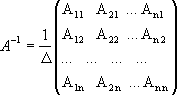,                                               (4.5)

где А _{i j} - алгебраические дополнения элементов a _{i j}.

Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

8) Метод обратной матрицы Систему линейных алгебраических уравнений AX = b умножим слева на матрицу, обратную к А. Система уравнений примет вид:

A^-1AX=A^-1b,  EX=A^-1b,  (E - единичная матрица) Таким образом, вектор неизвестных вычисляется по формуле X=A^-1b.