Ответы к зачёту по математике.

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. Определитель матрицы А обозначается как: det(A), |А| или Δ(A)

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

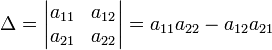
Для матрицы определитель задаётся рекурсивно:

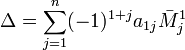,    где  — дополнительный минор к элементу a_1j. Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы такова:

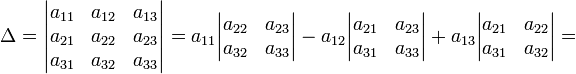
= a₁₁a₂₂a₃₃ − a₁₁a₂₃a₃₂ − a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ − a₁₃a₂₂a₃₁

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

Правило Саррюса

Дописывание двух первых строк или столбцов.

В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33

2) 1.Метод разложения определителя по строке(столбцу). Для реализации данного метода необходимо проделать следующее.

• Выбрать строку или столбец данного определителя. Выберем например 1 строку.

• Взять первый элемент этой строки и записать его в правой части равенства. Это будет первый сомножитель первого слагаемого результата.

• Мысленно вычеркнуть первую строку и первый столбец данной матрицы, поскольку на пересечений первой строки и первого столбца стоит выбранный элемент матрицы. В результате получится матрица на порядок меньшая исходной. Ее определитель нужно записать в результат вычисления в качестве второго сомножителя первого слагаемого разложения определителя.

• Число минус единица надо возвести в степень, которая определяется как сумма номера строки и номера столбца. Это будет третий сомножитель первого члена разложения определителя по первой строке.

• Второй и последующие члены разложения определяются аналогично.

Таким оразом данный метод сводит задачу вычисления определителя к задаче решения определителя более низкого порядка.

3) Система линейных алгебраических уравнений с неизвестными — это система уравнений вида

Здесь  — неизвестные, которые надо определить. Коэффициенты системы и её свободные члены предполагаются известными. Индексы коэффициента системы обозначают номера уравнения  и неизвестного , при котором стоит этот коэффициент.

Система называется однородной, если все её свободные члены равны нулю, , иначе — неоднородной.

Система называется квадратной, если число  уравнений равно числу  неизвестных.

Решение системы уравнений — совокупность чисел , таких что подстановка каждого  вместо  в систему обращает все её уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.

Решения и совместной системы называются различными, если нарушается хотя бы одно из равенств:

Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

4) Для системы n линейных уравнений с n неизвестными (над произвольным полем)

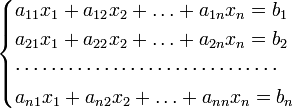
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

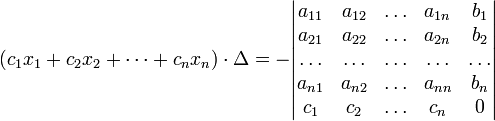
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.