5.3. Вектор скорости точки.
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
Рис. 5.3
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени ∆t:
∆t
= ∆
/∆t. (5.7)
Чтобы получить точную характеристику движения, вводят понятие о скорости точки в данный момент времени.
Скоростью точки в данный момент времени
t называется векторная
величина
при
стремлении промежутка времени ∆t
к нулю:
.
Предел отношения ∆
/∆t
при ∆t→0 представляет собой первую
производную от вектора ∆
по аргументу t и
обозначается, как и производная от
скалярной функции, символом d
/dt.
Окончательно получаем
(5.8)
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса - вектора точки по времени.
Так как предельным направлением секущей ММ1 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
Формула (5.8) показывает
также, что вектор скорости
равен отношению элементарного перемещения
точки d
,
направленного по касательной к траектории,
к соответствующему промежутку времени
dt.
Согласно выражению (5.2)
.
Дифференцируя вектор
по времени, на основании формулы (5.8)
получим:
(5.9)
Проекции скорости vx, vy, vz на оси координат будет:
(5.10)
Модуль и направление вектора скорости определяется формулами:
(5.11)
ˆ,
)=
ˆ,
)=
ˆ,
)=
(5.12)
5.4. Вектор ускорения точки.
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.
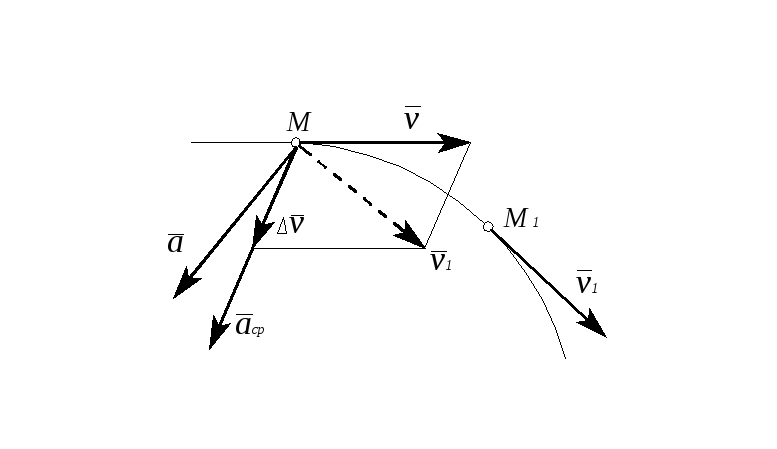
Рис. 5.4
Отношение приращения вектора скорости
∆
к соответствующему промежутку времени
∆t определяет
вектор среднего ускорения точки за
этот промежуток времени:
(5.13)
Вектор среднего ускорения имеет то же
направление, что и вектор, Δ
,
т.е. направлен в сторону вогнутости
траектории.
Ускорением точки в данный момент времени
t называется векторная
величина
,
к которой стремится среднее ускорение
при стремлении промежутка времени Δt
к нулю:
(5.13`)
или, с учетом равенства (5.8),
(5.14)
Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса - вектора точки по времени.
Пусть движение точки задано координатным способом. Модуль и направление ускорения точки, используя известные уравнения ее движения:
x=x(t), y=y(t), z=z(t).
Поскольку
применение формулы (5.14) дает:
(5.15)
Составляющие вектора
по осям х, y
и z будут:
(5.16)
или с учетом соотношений (5.10)
(5.17)
При известных проекциях ускорения на координатные оси модуль и направление вектора ускорения точки можно определить по формуле:
; (5.18)
ˆ,
)=
;
ˆ,
)=
;
ˆ,
)=
(5.19)
При естественном способе задания
движения положение точки на траектории
характеризуется законом s=s(t).
Определим ускорение точки. Для этого
представим вектор скорости по формуле:
.
В соответствии с определением (5.13΄) продиффе-ренцируем это соотношение по времени t, используя правило вычисления производной от произведения двух функций. Получим:
. (5.18)
Но по формуле
есть алгебраическая скорость точки, а
ее квадрат в любом случае есть положительная
величина:
Производная же от орта
по
дуговой координате s
равна n/ρ.
Следовательно, первое слагаемое в
выражении (5.18) представляет составляющую
вектора ускорения, направленную по
главной нормали к центру кривизны.
Обозначая ее через
,
можем записать:
.
(5.19)
Эта составляющая называется нормальным ускорением точки.
Вторую составляющую вектора ускорения
(5.18) обозначим через
.
Она представляет проекцию вектора
ускорения точки на касательную и
называется касательным ускорением
точки. С учетом обозначения
имеем:
.
(5.20)
Таким образом, ускорение точки при естественном способе задания движения будет:
,
(5.21)
где составляющие
и
определены формулами (5.19)-(5.20).
Модуль вектора ускорения равен:
,
(5.22)
а его направление определится по формуле:
.
(5.23)