1. Бернулли;

2. сложения вероятностей;

3. *Пуассона;

4. Муавра-Лапласа.

14. Монета брошена 2N раз (N велико). Вероятность того, что “герб” выпадет N раз, предпочтительнее вычислять с использование

1. *локальной теоремы Муавра-Лапласа

2. формулы Бернулли

3. формулы Пуассона

4. формулы сложения вероятностей.

15. При проведении контроля качества среди 1000 случайно отобранных деталей 5 оказалось бракованными. Среди 25000 деталей бракованных окажется:

1. 535

2. 250

3. * 125

4. 50

16. При проведении контроля качества среди 1000 случайно отобранных деталей 5 оказалось бракованными. Среди 50000 деталей бракованных окажется:

1. 535

2. * 250

3. 125

4. 50

17. Число m₀ наступления события в серии из n испытаний называется наивероятнейшим числом, если

1. это число является наибольшим среди всех остальных;

2. оно совпадает с числом испытаний n;

3. *оно соответствует наибольшей вероятности в данной серии испытаний;

4. событие, соответствующее этому числу, достоверно.

18. Наивероятнейшее число наступления события m₀ находится в интервале

1. 

2. *

3. 

4. 

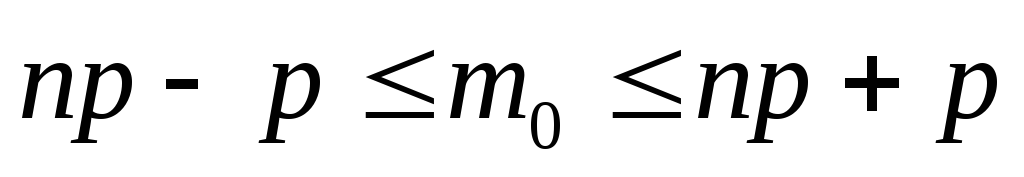
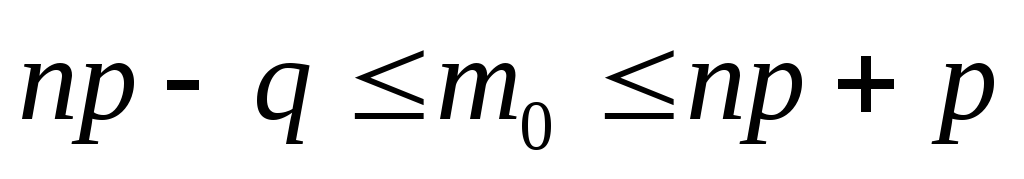
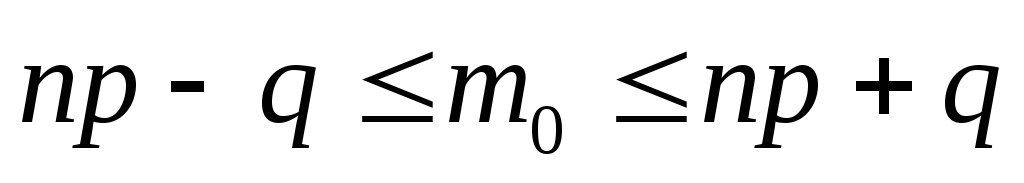
19. Вероятность попадания стрелком в цель равна 0,7. Сделано 10 выстрелов. Наивероятнейшее число попаданий в цель:

1. *7

2. 15

3. 18

4. 20

5. 25

20. Вероятность попадания стрелком в цель равна 0,7. Сделано 15 выстрелов. Наивероятнейшее число попадания в цель:

1. *11

2. 14

3. 18

4. 20

5. 25

21. Вероятность попадания стрелком в цель равна 0,8. Сделано 10 выстрелов. Наивероятнейшее число попаданий в цель:

1. *8

2. 10

3. 15

4. 20

5. 25

22. Произведение меньшей, чем ½, вероятности появления события в одном испытании и числа произведенных испытаний в схеме Бернулли равно 127,45. Наивероятнейшее число появления события равно

1. 127 (*)

2. 128

3. 126

4. 128,45

5. 127,95

23. Вероятность того, что в небольшом числе n независимых испытаний с постоянной вероятностью р появления события в каждом из них событие А наступит m раз определяется по формуле

1. полной вероятности

2. Бернулли (*)

3. нормального закона распределения

4. Пуассона

5. Байеса

24. При большом числе независимых испытаний и постоянной, близкой к 0,5 вероятности р появления события в каждом из них вероятность наступления события m раз определяется по формуле

1. Байеса

2. Бернулли

3. нормального закона распределения (*)

4. полной вероятности

5. Пуассона

25. Наиболее вероятное число горожан, родившихся 29 февраля, при населении города 150 тыс. жителей:

1. * 103

2. 150

3. 125

4. 250

2. Случайные величины и законы их распределения

2.1. Дискретные случайные величины

2.1.1. Ряд распределения и интегральная функция распределения дискретной случайной величины

1. С помощью интегральной функции распределения можно задать

1. дискретную случайную величину

2. непрерывную случайную величину

3. случайное событие

4. интервальную величину

	интервальными
	непрерывными
Случайные величины могут быть	дискретными
	точечными