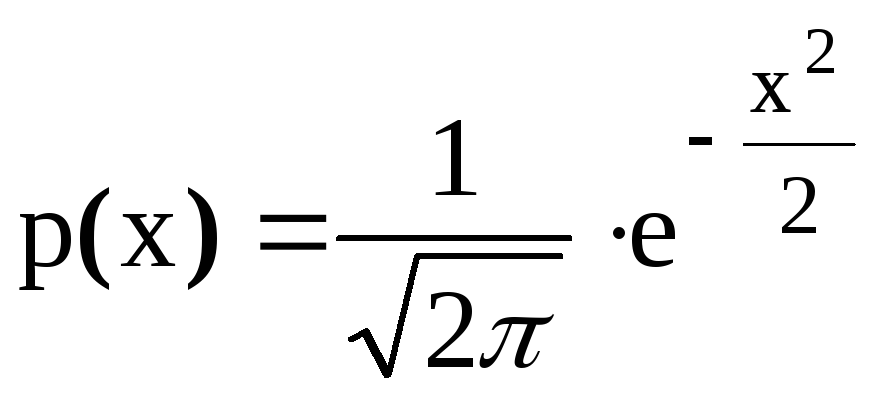- •Случайные события и их вероятности
- •Случайные события и действия над ними
- •Виды событий
- •Событие, ……… достоверному событию, является невозможным.
- •Событие, противоположное ………событию, является достоверным.
- •1.2.Вероятности событий
- •1.2.1.Вероятности простых событий
- •Вероятность выпадения четного числа очков при бросании игральной кости:
- •1.2.2. Вероятности сумм и поизведений событий
- •Несовместные
- •Независимые
- •1.2.3. Формула полной вероятности и формула Байеса
- •1.2.4. Повторные независимые испытания. Асимптотические формулы теории вероятностей
- •Бернулли;
- •Бернулли (*)
- •Бернулли
- •Дискретные случайные величины:
- •Закон распределения вероятностей числа попаданий в мишень при двух независимых выстрелах, если вероятность попадания при каждом выстреле равна 0.8, имеет вид:
- •Монета подбрасывается 2 раза. Закон распределения случайной величины – числа появления орла.
- •В коробке 3 карандаша, из них 1 красный, 2синих. Извлекаются 2 карандаша. Закон распределения числа синих карандашей среди извлеченных:
- •Законы распределения дискретной случайной величины имеют вид:
- •Случайная величина X задана интегральной функцией распределения:
- •Дана интегральная функция распределения случайной величины X:
- •2.1.2. Числовые характеристики дискретной случайной величины
- •Закон распределения случайной величины представлен в таблице
- •Закон распределения случайной величины представлен в таблице
- •Закон распределения случайной величины представлен в таблице
- •Закон распределения случайной величины X задан рядом распределения
- •Закон распределения случайной величины X задан рядом распределения
- •Дан закон распределения дискретной случайной величины:
- •Дан закон распределения дискретной случайной величины:
- •Дан закон распределения дискретной случайной величины
- •Функция Лапласа:
- •Выражения, справедливые для нормированной нормальной случайной величины X:
- •Бернулли
- •Бернулли
- •Бернулли
- •Бернулли
- •Соответствие между формулой и определением
- •Соответствие между формулой и определением
- •Соответствие между формулой и определением
-
Нормальным
-
равномерным
-
Пуассона
-
Бернулли
-
Распределение, описываемое формулой
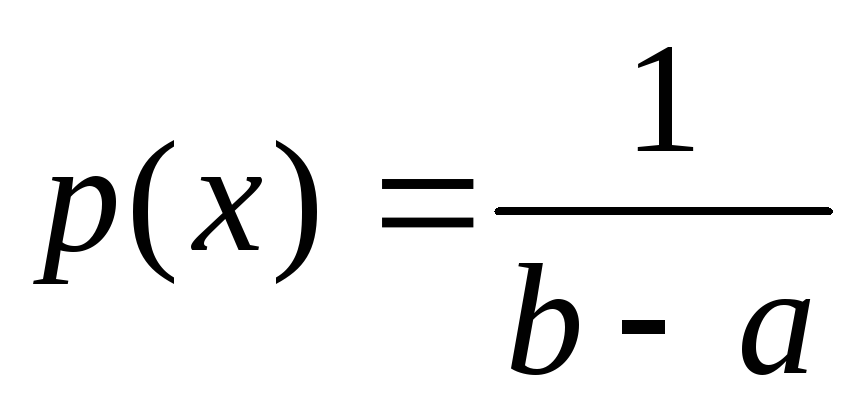 выражает… закон распределения
выражает… закон распределения
-
Нормальным
-
равномерным
-
Пуассона
-
Бернули
-
Распределение с плотностью, описываемой формулой
![]() выражает……. закон распределения
выражает……. закон распределения
-
Нормальный
-
равномерный
-
t-распределение
-
Пуассона
-
Бернулли
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Плотность вероятности случайной величины X, распределенной по показательному закону с параметром λ=5, имеет вид:
-
f(x)=λ·eλx;
-
f(x)=
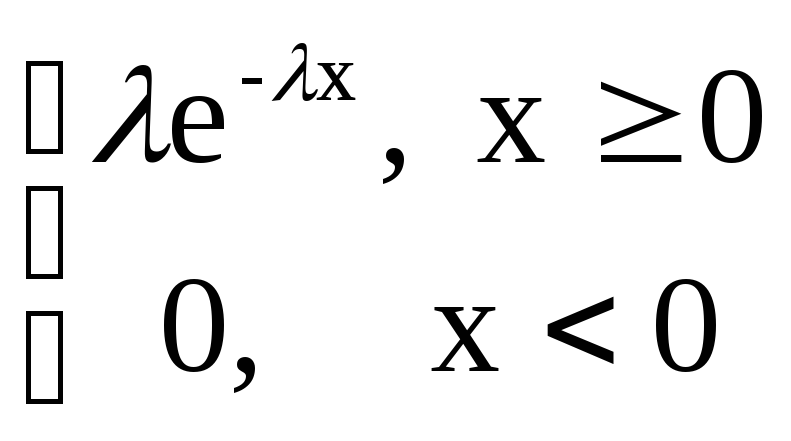 .
.
-
f(x)=
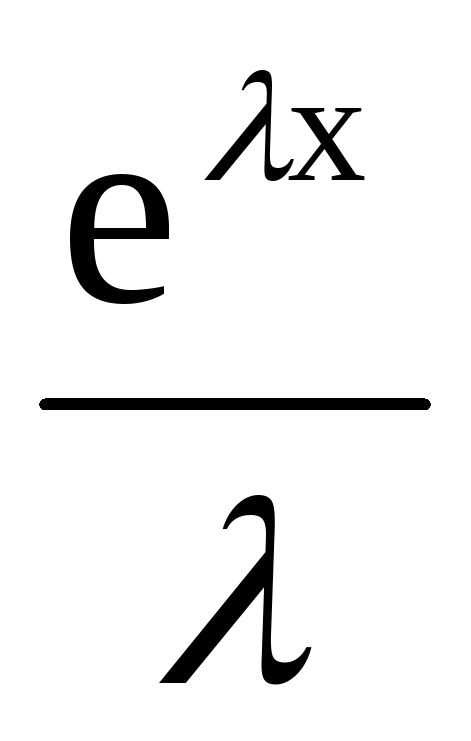 ;
; -
f(x)=
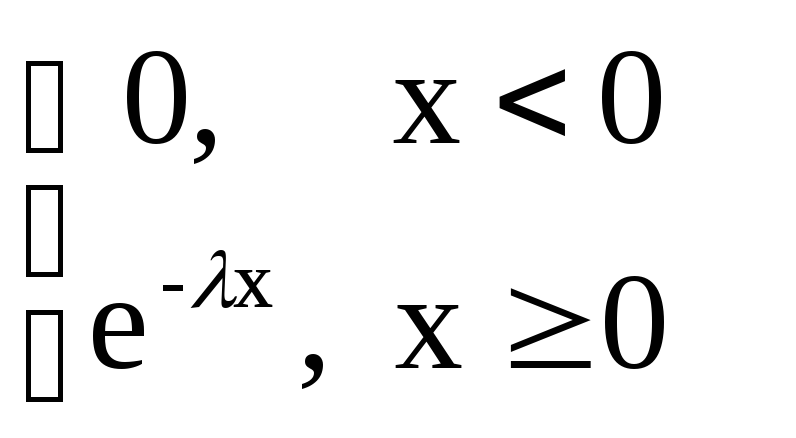 .
.
-
Случайная величина X имеет показательное распределение f(x)=
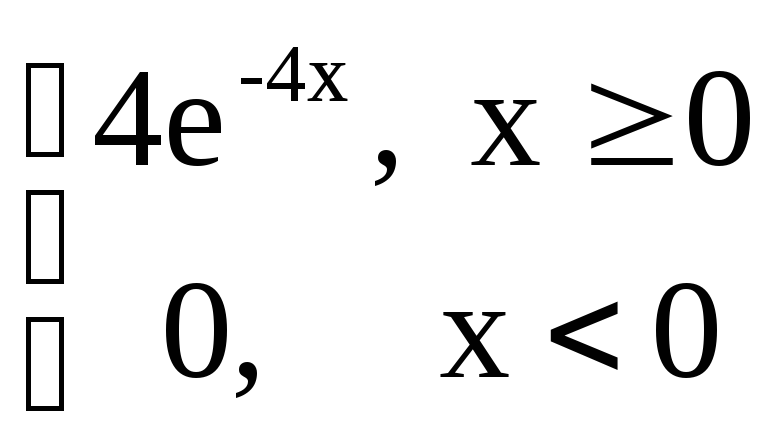 .
Математическое ожидание X
равно:
.
Математическое ожидание X
равно:
-
MX=4;
-
MX=0,5;
-
MX=0,25;
-
MX=-0,25.
-
Случайная величина X имеет показательное распределение f(x)=
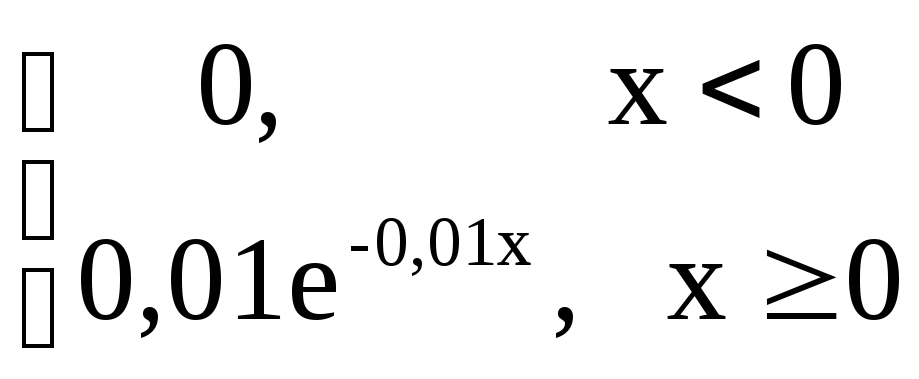 .
.
Среднее квадратичное отклонение σx равно:
-
σx=10;
-
σx=100;
-
σx=0,01;
-
σx=0,1.
-
Соответствие между формулой и определением
|
|
|
|
|
|
|
|
-
Соответствие между формулой и определением
|
|
|
|
|
|
|
|
-
Соответствие между формулой и определением
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
B |
B |
A |
B |
B |
B |
A |
B |
B |
BCD |
AB |
AA, BB, CC, DD |