4.2. Уравнение Шредингера
Микрочастицы обладают волновыми свойствами, поэтому классическая механика не может дать правильного описания их поведения. Квантовая механика создана Э.Шредингером, В. Гайзенбергом, П. Дираком и другими учеными. Основное уравнение нерелятивистской квантовой механики в 1926 году сформулировано Э. Шредингером.
Нестационарное (общее) уравнение Шредингера:
,
где
– оператор Лапласа (записан в декартовых
координатах);
– потенциальная энергия частицы в
силовом поле;
– масса микрочастицы;
;
–
постоянная Планка;
– мнимая единица. Уравнение справедливо
для любой частицы, движущейся с малой
(по сравнению со скоростью света)
скоростью.
Рассмотрим
свободно движущуюся частицу, которой,
согласно идее де Бройля, сопоставляется
плоская волна. Уравнение плоской волны,
распространяющейся вдоль оси
,
имеет вид:
.
Это
выражение в комплексном виде:
,
где
– полная энергия частицы;
– длина волны;
– волновое число.
Получим для одномерного случая свободно движущейся частицы волновую функцию:
.
Зависимость энергии от импульса:
.
(26)
Дифференцируя
функцию
один раз по
и дважды по
,
получаем:
;
.
Из
этих соотношений найдем
и
через функцию
и ее производную:
,
.
Подставляя эти выражения в (26), получаем дифференциальное уравнение:
.
Если
направление волны не совпадает с осью
,
фаза колебаний будет зависеть от
координат (
).
Для этого случая уравнение имеет вид:
.
Учитывая (26), получаем стационарное уравнение для свободной частицы:
.
Это
уравнение совпадает с уравнением
Шредингера для случая
,
так как мы рассматривали свободную
частицу.
Если
частица движется в силовом поле,
характеризуемом потенциальной энергией
,
то полная энергия
складывается из кинетической и
потенциальной энергий.
Полная энергия микрочастицы:
,
где
и не зависит явно от времени.
Уравнение Шредингера для стационарных состояний:
.
4.3. Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»
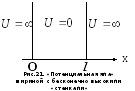
Проведем
качественный анализ решений уравнения
Шредингера применительно к частице в
одномерной прямоугольной «потенциальной
яме» шириной
с бесконечно высокими «стенками». Такая
«яма» описывается потенциальной энергией
вида (для простоты принимаем, что частица
движется вдоль оси
)
(рис.21):
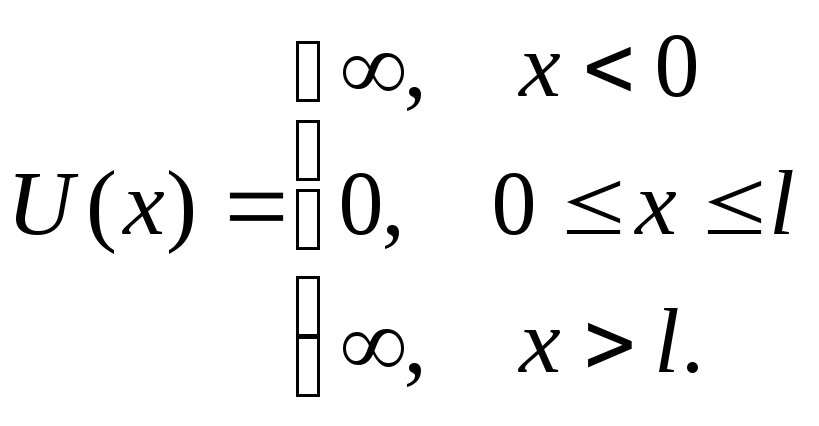
Поскольку
функция
зависит от одной координаты
,
уравнение Шредингера имеет вид:
.
Так
как «стенки» ямы бесконечно высокие,
то частица не проникает за пределы
«ямы», поэтому вероятность обнаружения
(а, следовательно, и волновая функция)
за пределами «ямы» равна нулю. Из условия
непрерывности функции
на границах «ямы» волновая функция
также должна обращаться в нуль.
Следовательно, граничные условия:
|
|
(27)
(28) |
В
пределах «ямы»
уравнение Шредингера имеет вид:
.
Введем
обозначение
,
тогда получим уравнение, известное из
теории колебаний (уравнение свободных
незатухающих колебаний):
.
Решение такого уравнения имеет вид:
.
(29)
С
учетом условия (27) из уравнения (29)
следует:
.
С учетом условия (28) из уравнения (29)
следует:
,
что возможно лишь в случаях
(
=1,
2, 3…).
Следовательно,
решение уравнения Шредингера имеет
физический смысл не при всех значениях
энергии
,
а лишь при значениях энергий удовлетворяющих
соотношению:
.
Поскольку
,
получаем
,
т.е.
.
Отсюда
(
=1,2,3…).
Таким
образом, уравнение Шредингера, описывающее
движение частицы в «потенциальной яме»
с бесконечно высокими «стенками»,
удовлетворяется только при собственных
значениях
,
зависящих от целого числа
.
Следовательно, энергия
частицы не может быть произвольной, а
принимает лишь определенные дискретные
значения, т.е. квантуется. Квантовые
значения энергии
называются уровнями энергии, а число
,
определяющее энергетические уровни
частицы, называется квантовым числом.
Оценим энергетический интервал между двумя соседними уровнями:
,
,
.
Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию частицы никаких ограничений не накладывает.
Определим
коэффициент
в уравнении
.
С
учетом
.
(30)
Для
нахождения коэффициента
воспользуемся условием нормировки:
.
Подставив в это выражение (30), получаем:
.
Значение
интеграла можно получить, умножив
среднее значение
(равное 1/2) на длину промежутка
.
В результате получаем:
,
.
С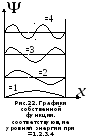
обственные
функции имеют вид:
.
Графики
этой функции, соответствующие уровням
энергии при
=1,2,3,4,
изображены на рис.22. Из рисунка видно,
что частица в состоянии с
=2
не может быть обнаружена в середине ямы
и вместе с тем одинаково часто бывает
как в левой, так и в правой половинах
ямы. Такое поведение частицы не совместимо
с представлением о траекториях. Согласно
классическим представлениям, все
положения частицы в яме равновероятны.