
КОЛЕБАНИЯ И ВОЛНЫ
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КОЛЕБАНИЯ И ВОЛНЫ
Учебное пособие
Pостов-на-Дону 2009
УДК 530.1
С 74
Авторы: Егорова С.И., Егоров И.Н., Кунаков В.С., Лемешко Г.Ф., Наследников Ю.М.
Колебания и волны: Учеб. пособие.- Ростов н/Д: Издательский центр ДГТУ,2009.- 55 с.
В данном пособии рассматривается теория механических и электрических колебаний как единый процесс. Колебания излагаются в рамках модели одномерного гармонического осциллятора.
Учебное пособие (включая электронную версию) предназначено для студентов, изучающих физику, для самостоятельной работы в период подготовки к рейтинговому контролю и экзамену, а также при подготовке к лабораторным работам.
Печатается по решению редакционно-издательского совета Донского государственного технического университета.
Научный редактор д-р техн. наук, проф. Кунаков В.С..
©Егорова С.И., Егоров И.Н., Кунаков В.С. Лемешко Г.Ф., Наследников Ю.М.
.
©Издательский центр ДГТУ, 2009
2
Предисловие
Учебное пособие составлено в соответствии с рабочей программой по физике. Оно не может и не должно заменить учебник и предназначено для того, чтобы помочь студентам при подготовке к лабораторным работам и экзаменам.
Колебания излагаются в рамках модели одномерного гармонического осциллятора. Тем самым задаѐтся общий подход к теории колебаний различной физической природы.
Для упрощения вывода решения дифференциального уравнения затухающих колебаний введѐн энергетический подход к рассеянию энергии.
Решение дифференциального уравнения вынужденных колебаний проводится геометрически через векторные диаграммы, что позволяет избежать сложных математических выкладок.
При рассмотрении автоколебаний особое внимание уделяется выделению основных элементов автоколебательной системы.
Общая теория колебаний позволяет студентам осознать значимость теории колебаний не только в физике и технике, но и в понятии цикла, как основы мироздания.
3
Общие сведения о колебаниях. Одномерный классический гармонический
осциллятор
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Рассмотрим механические колебания.
В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Силу, под действием которой происходит колебательный процесс, называют возвращающей силой, так как она стремится вернуть тело или материальную точку в положение равновесия.
Свободные колебания совершаются системой, выведенной из положения равновесия.
Собственными называются свободные колебания без учѐта сил сопротивления (без затухания).
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером служат колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.
Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счѐт энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение.
При параметрических колебаниях за счѐт внешнего воздействия происходит периодическое изменение какого-либо параметра системы, например, длины нити, к которой подвешен шарик, совершающий колебания.
Простейшими являются гармонические колебания, при которых колеблющаяся величина (например, отклонение маятника)
4
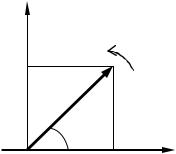
изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническому, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний. Гармонические колебания удобно представить в виде круговой диаграммы (рис.1). Пусть
точка |
B движется по окружности радиусом |
A . Еѐ положение задаѐтся |
|
|
|
|
|
радиус-вектором |
A . Положение равновесия задаѐтся точкой O . Радиус- |
||
|
|
|
|
вектор |
A равномерно вращается с угловой скоростью 0 . Проекции |
||
|
|
|
|
радиус-вектора |
A на оси OX или OY задаются математическими |
||
выражениями (уравнениями) гармонических колебаний: |
|||
|
|
x = Acos ω0t + α |
(1) |
|
|
y = Asin ω0t + α |
(2) |
y
0
y |
|
B |
|
||
|
A |
|
|
|
0t |
|
|
|
O |
0 |
x |
Рис. 1
= ω0t + α , характеризующий
|
Мы |
|
будем |
||
|
использовать |
|
уравнение |
||
|
гармонических |
колебаний |
в |
||
|
виде (1). |
Координата |
x |
||
|
задаѐт |
|
|
значение |
|
|
колеблющейся |
|
величины. |
||
|
Величина |
A |
– |
амплитуда |
|
|
колебаний, |
|
|
т.е. |
|
|
максимальное |
|
отклонение |
||
|
колеблющейся |
|
точки |
от |
|
|
положения |
|
|
равновесия. |
|
x |
Величина |
ω0 , |
равная числу |
||
|
колебаний |
за |
|
время |
2π |
|
секунды, |
|
|
называется |
|
|
циклической |
|
частотой. |
||
|
Аргумент |
|
|
косинуса |
|
значение колеблющейся |
величины в |
||||
момент времени t , называется фазой колебаний. Фаза колебаний α , соответствующая начальному моменту времени, называется начальной
фазой колебаний. Время одного полного колебания T0 называется периодом колебаний. Число колебаний ν0 за время, равное одной
5

секунде, называется частотой колебаний.
0 2v0 2 / T0 .
Скорость колеблющейся точки находится дифференцированием выражения (1) по времени:
= |
dx |
= ω Asin ω t + α Acos( t / 2) (3) |
|||||||||
|
|
||||||||||
|
|
|
dt |
|
|
0 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференцируя вторично, получаем ускорение: |
|
|
|||||||||
a = |
d |
= |
d 2 x |
= ω2 |
Acos ω t + α 2 Acos( |
t ) . (4) |
|||||
|
|
||||||||||
|
dt |
|
|
|
dt 2 |
0 |
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
a 2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x t , t ,a t . Скорость |
|
|
На |
|
рис. 2 представлены |
зависимости |
|||||||
опережает смещение на / 2 , ускорение находится в противофазе по отношению к смещению.
x
A
0 t
t
A
0 A
0 t0 A
t0 A
a
02 A
0 t
t
02 A
Рис. 2
6
Каждое конкретное колебание характеризуется определенным значением
амплитуды A и начальной фазы α . Определим их
значения |
из |
начальных |
условий |
(t 0) . В этом |
|
случае |
|
x0 = Acosα , |
0 = ω0 Asinα . Отсюда следует, что
2
A x 2 0 ,
0 02
tg 0 .
x0 0
Выведем дифференциальное уравнение гармонических колебаний. Из выражения (4) следует, что
d 2 x |
= ω2 x |
или |
|
d 2 x |
ω2 x 0 |
. (5) |
dt 2 |
0 |
|
|
dt 2 |
0 |
|
|
|
|
|
|
Уравнение (5) является дифференциальным уравнением
гармонических колебаний. Это уравнение является общим уравнением, описывающим гармонические колебания. Его решением являются функции (1) или (2). Следовательно, можно сказать, что гармоническими называются колебания, совершаемые по закону синуса или косинуса.
Колебательные системы, описываемые уравнением (5)
называются одномерным классическим гармоническим осциллятором. Модель одномерного классического гармонического осциллятора оказывается справедливой не только для механических, но и других видов собственных незатухающих колебаний. В различных разделах физики используется единый математический язык описания гармонических колебаний.
Рассмотрим конкретные примеры гармонических осцилляторов в механике.
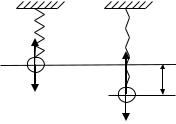
Пружинный маятник (рис. 3)
Применим к движению груза на пружине второй закон Ньютона:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
mg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ma |
|
= F |
, где F = kx - сила упругости: a |
|
= |
d 2 x |
= |
k |
x , |
||
x |
x |
|
|
||||||||
|
x |
|
x |
|
dt |
2 |
|
m |
|||
|
|
|
|
|
|
|
|
||||
7
|
|
d 2 x |
|
|
k |
|
x 0 . |
(6) |
|||||||
|
|
dt 2 |
|
m |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Сравнивая (5) и (6), получаем: |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 = |
|
|
|
k |
|
|
|
(7) |
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
m |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||||
|
T = |
2π |
= 2π |
m |
|
(8) |
|||||||||
|
|
||||||||||||||
|
0 |
|
ω0 |
|
|
k |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
Мы нашли собственную циклическую частоту (7) и период колебаний (8) груза на пружине.
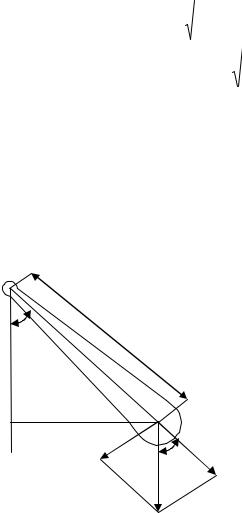
Физический маятник (рис. 4)
Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения ( -
мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой
составляющую силы тяжести, приложенную в точке C :
0 |
|
F = mgsinα |
|
|
Момент |
этой |
силы |
||
|
относительно оси O равен:
|
d |
|
M = Fl = mgdsinα , где |
||
|
l d sin - |
|
|||
|
|
|
плечо силы |
||
|
|
|
F относительно оси O , знак |
||
|
|
|
минус соответствует тому, что |
||
|
|
|
момент |
M стремится вернуть |
|
|
|
|
маятник |
в |
положение |
|
C |
|
равновесия, |
аналогично |
|
|
|
квазиупругой силе. |
|||
F |
|
|
В соответствии с уравнением |
||
|
|
|
динамики |
вращательного |
|
|
|
движения |
|
||
|
|
Fn |
|
||
Рис. 4. |
|
|
|
|
|
|
|
|
|
|
|
mg
8

M = I , где |
d |
2 |
- |
|
угловое ускорение, I - момент инерции |
||||
dt 2 |
|
||||||||
|
|
|
|
|
|
|
|||
маятника относительно оси О. Получаем |
|||||||||
|
I |
d 2 |
|
mgd sin . (9) |
|||||
|
dt 2 |
||||||||
|
|
|
|
|
|
|
|
||
Ограничившись малыми колебаниями sinα ~ α , после преобразований |
|||||||||
получаем уравнение (9) в виде: |
|||||||||
|
|
|
d 2 |
|
+ |
mgd |
= 0 |
(10). |
|
|
|
|
dt 2 |
|
|
||||
|
|
|
|
|
I |
|
|||
Сравнив выражения (5) и (10) мы видим их математическую аналогию, что позволяет записать выражения для циклической частоты и периода колебаний физического маятника:
|
ω0 = |
|
mgd |
|
(11) |
||||||||
|
|
|
|
|
|
||||||||
|
|
I |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
T = |
2π |
= 2π |
|
|
|
I |
|
|
, (12) |
||||
|
|
|
|
|
|
||||||||
0 |
|
ω0 |
|
|
|
|
mgd |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
где d -расстояние от центра тяжести до оси вращения.
Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны. Колебания приближенно изохронны, когда угловая амплитуда колебаний не превышает нескольких градусов. При больших амплитудах изохронность нарушается. На свойстве изохронности колебаний маятника основано его применение в часах.
Математический маятник (рис. 5)
|
|
|
|
|
l |
|
|
|
|
m |
|
|
F |
|
|
Рис. 5 |
|
|
|
|
F |
|
|
|
mg |
n |
9 |
|
|
||
|
|
|
Математический маятник является частным случаем физического маятника. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, к которой подвешена
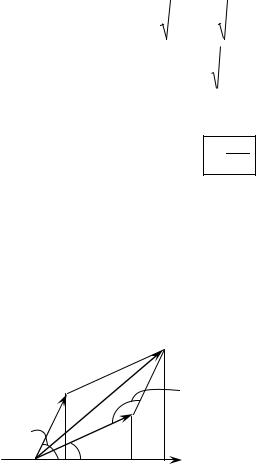
масса, сосредоточенная в одной точке. Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае
математического маятника d l, I ml 2 ,где l -длина математического маятника. Тогда формулы (11) и (12) запишутся в виде:
ω = |
|
mgl |
|
= |
|
g |
|
(13) |
|
|
|||||||
0 |
|
ml 2 |
l |
|
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
T = |
2π |
= 2π |
l |
|
(14) |
||
|
|
||||||
0 |
ω0 |
|
|
g |
|
|
|
|
|
|
|
|
|
||
Сравнивая формулы (12) и (14), заключаем, что физический маятник колеблется с периодом математического маятника, длина которого
l = mdI ,
называется приведенной длиной физического маятника.
Сложение колебаний
Векторная диаграмма
Гармонические колебания удобно представлять в виде векторных (круговых) диаграмм. В этом случае гармоническое колебание совершает проекция радиус-вектора,
|
|
|
|
|
|
|
равного |
по |
модулю |
|
|
|
|
A |
|
C |
|
амплитуде колебаний A . |
|||
|
|
|
|
|
2 1 |
|
Воспользуемся |
методом |
||
|
|
|
|
векторных |
диаграмм при |
|||||
|
A2 |
|
|
|
сложении |
гармонических |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
колебаний |
одинакового |
|||
2 |
|
|
A1 |
|
|
|
направления |
с |
||
|
1 |
B |
|
|
|
одинаковыми частотами. |
||||
|
|
|
|
x |
|
Смещение |
|
x |
||
O |
x |
|
x1 |
x |
|
колеблющегося |
тела |
|||
2 |
|
|
равно |
сумме |
смещений |
|||||
|
|
|
|
|
|
|||||
|
Рис. 6 |
|
|
|
|
x1 |
и |
x2 , |
которые |
|
|
|
|
|
|
|
|
|
|
записываются |
|
|
|
|
|
|
10 |
|
|
|
|
|
