
КОЛЕБАНИЯ И ВОЛНЫ
.pdfследующим образом: |
|
|
|
|
|
|
x1 = A1cos ω0t +α1 |
и |
x2 = A2cos ω0t + α2 |
(16) |
|
|
|
|
|
|
|
|
|
|
Представим оба колебания с помощью векторов |
A1 |
и |
A2 |
(рис. |
||
6). Построим по правилам сложения векторов результирующий вектор |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x равна сумме |
A . Легко видеть, что проекция этого вектора на ось |
||||||||||||
проекций слагаемых |
векторов |
x = x1 + x2 . |
Следовательно, проекция |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
вектора A представляет собой результирующее колебание. |
||||||||||||
Этот вектор вращается с той же угловой скоростью (циклической |
||||||||||||
частотой) ω0 , как |
|
|
|
|
|
|
|
|
|
|
||
и |
векторы A1 |
и |
A2 , |
так что |
результирующее |
|||||||
движение будет гармоническим колебанием с частотой |
ω0 , амплитудой |
|||||||||||
A и начальной фазой α . Из построения видно, что |
|
|||||||||||
A2 = A2 |
+ A2 |
2A A cos π α |
2 |
α = |
|
|||||||
1 |
|
2 |
|
|
1 |
2 |
|
|
|
1 |
(17) |
|
A2 + A2 |
+ 2A A cos α |
|
α |
|
|
|
||||||
2 |
|
|
|
|||||||||
1 |
2 |
|
1 |
2 |
|
1 |
|
|
|
|||
|
tgα = |
A1sinα1 + A2sinα2 |
. (18) |
|
||||||||
|
A1cosα1 + A2cosα2 |
|
||||||||||
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения вращающихся векторов.
Проанализируем выражение (17) для амплитуды:
а) если разность фаз колебаний α2 α1 = 0 , т.е. колебания происходят в одинаковой фазе, то амплитуда результирующего колебания равна A = A1 + A2 ;
б) |
если разность фаз колебаний α2 α1 = ±π , т.е. |
колебания |
находятся |
в противофазе, то амплитуда результирующего |
колебания |
A = A1 A2 . |
|
|
Биения
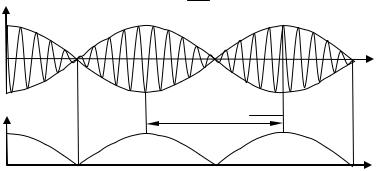
Особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биением.
11
Пусть |
частота одного |
колебания |
ω1 = ω , |
а частота |
второго |
колебания |
ω2 = ω+ Δω , |
причем, |
Δω ω . |
Амплитуды |
обоих |
колебаний полагаем одинаковыми и равными A . Для упрощения расчетов полагаем начальные фазы колебаний равными нулю. Тогда уравнения складываемых колебаний будут иметь следующий вид:
x1 = Acosωt
x2 = Acos ω+ Δω t
Складывая эти выражения и применяя тригонометрическую формулу для
|
|
|
|
|
|
|
||
суммы косинусов cos cos |
2 cos |
|
cos |
|
|
, |
||
|
|
|
||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
Δω |
|
|
|
|
|
|
получаем x = x1 + x2 |
= 2Acos |
|
t cosωt |
|
|
(19). |
||
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
(во втором множителе пренебрегли членом / 2 по сравнению с ).
График функции (19) для случая / = 10 изображен на рисунке
7.а.
x
а)
б) |
Амплитуда |
|
Т 2 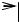

t
Т б 2
б 2
t
Рис. 7
Заключенный в скобки множитель в формуле (19) изменяется гораздо
12

медленнее, чем второй множитель, так как Δω ω . Это дает нам основание рассматривать колебание (19) как гармоническое колебание
частоты ω , амплитуда которого изменяется по некоторому закону. Выражением этого закона не может быть множитель, стоящий в скобках,
так как он изменяется от 2A до 2A , в то время, как амплитуда по определению – величина положительная. График амплитуды показан на рис 7.б. Аналитическое выражение амплитуды, очевидно, имеет вид:
|
|
Δω |
|
|
||
Aбиений |
= 2Acos |
|
t |
. |
(20) |
|
|
|
2 |
|
|
|
|
Функция (20) – периодическая функция с частотой в два раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с
частотой Δω . Заменяя в выражении (19) амплитуду через значение (20), получаем уравнение биений:
|
Δω |
|
|
x = 2Acos |
|
t cosωt |
(21) |
|
2 |
|
|
Сложение взаимно перпендикулярных колебаний
Допустим, что материальная точка (тело) может совершать
колебания как вдоль оси X , так и вдоль перпендикулярной оси Y . Если возбудить оба колебания, материальная точка будет двигаться по некоторой криволинейной траектории, форма которой зависит от разности фаз колебаний. Выберем начало отсчета времени так, чтобы начальная фаза одного колебания была равна нулю. Тогда уравнения запишутся следующим образом:
x = Acos ωt
y = Bcos ωt + α , (22)
где α - разность фаз складываемых колебаний, A и B — амплитуды
колебаний.
Выражения (22) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (22)
13

параметр t . Из первого уравнения следует, что |
|
||
cos ωt = x / A , |
(23) |
||
следовательно, |
|
||
sin ωt = ± |
|
|
|
1 x2 / A2 |
(24). |
||
Теперь развернем косинус во втором уравнении из (22) по формуле для косинуса суммы ( y / B cos t cos sin t sin ) и подставим в
него вместо cos ωt |
и sin ωt их значения (23) и (24). В результате |
|||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
= |
x |
cosα sinα |
1 |
x2 |
. |
||
|
|
|
|
|
||||||
|
B |
A |
|
|
A2 |
|||||
Перенесем все члены без корня в левую часть уравнения и возведем его в квадрат. После несложных преобразований получим уравнение эллипса, оси которого повернуты относительно координатных осей:
|
x2 |
+ |
y 2 |
2 |
xy |
cosα = sin 2 α |
(25) |
|
A2 |
B2 |
AB |
||||
|
|
|
|
|
Ориентация эллипса и величина полуосей зависят довольно сложным образом от амплитуд A и B и разности фаз .
Рассмотрим некоторые частные случаи. 1. Разность фаз α = 0 .
|
|
|
|
x |
|
y |
2 |
|
В этом случае уравнение (25) |
примет вид |
|
|
|
= 0 , |
|||
|
|
|||||||
|
|
|
|
A |
|
B |
|
|
откуда получается уравнение прямой: |
|
|
|
|
|
|||
y = |
B |
x |
(26). |
|
|
|
|
|
|
|
|
|
|
|
|||
|
A |
|
|
|
|
|
|
|
Результирующее движение является гармоническим с частотой
ω и амплитудой 
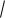 A2 + B2 (рис 8).
A2 + B2 (рис 8).
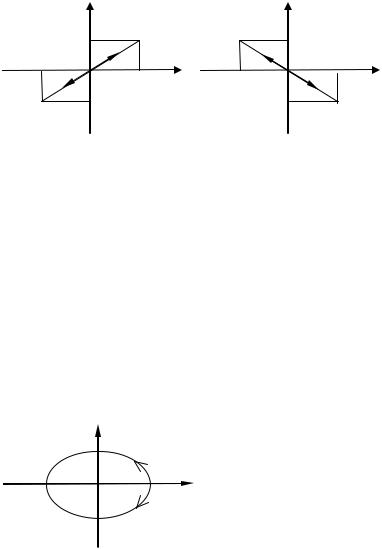
2.Разность фаз α = ±π . В этом случае уравнение (25) примет вид
14
|
y |
|
|
|
|
y |
|
|
|
A |
|
|
|
|
A |
|
|
|
B |
|
|
|
B |
|
|
|
B |
O |
x |
|
|
|
O |
B |
x |
|
|
|
|
|
|
|
||
|
A |
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
Рис. 8 |
|
|
|
|
Рис. 9 |
|
|
|
|
x |
|
y |
2 |
|
|
|
|
|
|
+ |
|
|
= 0 , |
|
|
|
|
|
|
|
||||
|
|
A |
|
B |
|
|
|
|
откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис.9):
y = |
B |
x . |
(27) |
|
|||
|
A |
|
|
3.Разность фаз α = / 2 .
Уравнение (25) переходит в уравнение эллипса,
приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний (рис.10):
|
|
x2 |
+ |
y 2 |
= 1. |
|
(28) |
|
|
|
|
|
A2 |
B2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
При |
равенстве |
|
|
y |
|
|
|
|
амплитуд A и B эллипс |
||||
|
|
|
|
|
вырождается |
в окружность. |
||||
|
|
2 |
|
Случаи |
α = / 2 |
и |
||||
B |
|
|
|
|
|
|||||
|
|
|
|
|
α = / 2 |
отличаются |
||||
A 1 |
|
|
|
|||||||
|
|
|
x |
|||||||
O |
|
|
|
|
|
направлением |
движения |
по |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
эллипсу или по окружности. |
|
||
|
|
|
|
|
|
|
Если α = / 2 , |
|||
|
|
2 |
|
|
||||||
|
|
|
уравнения (22) можно |
|
||||||
Рис. 10 |
записать следующим образом: |
|
|
|
15 |
|
|
|
|
|
x = Acosωt |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y = Bsinωt . |
|
|
|
|
|
|
|
|
|||
В |
момент |
t 0 |
тело |
находится |
в |
точке |
|
1 (рис 10). В |
||||||||
последующие моменты времени, координата |
x |
уменьшается, |
а |
|||||||||||||
координата |
y |
становится |
отрицательной. |
Следовательно, |
движение |
|||||||||||
совершается по часовой стрелке. |
|
|
|
|
|
|
|
|
|
|
|
|||||
Если α = / 2 , уравнения колебаний имеют вид: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
x = Acosωt . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y = Bsinωt |
|
|
|
|
|
|
|
|
||
Отсюда можно заключить, что движение происходит против |
||||||||||||||||
часовой стрелки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из |
сказанного |
|
следует, |
что |
равномерное |
движение |
по |
|||||||||
окружности |
радиусом |
R |
с |
угловой |
скоростью |
ω |
может |
быть |
||||||||
представлено как сумма двух взаимно перпендикулярных колебаний: |
|
|||||||||||||||
|
|
|
|
x = Rcosωt |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
y = ±Rsinωt . |
|
|
(29) |
|
|
|
|
|
||||
(знак «+» в выражении для |
y соответствует движению против часовой |
|||||||||||||||
стрелки, знак «-» – по часовой стрелке). |
|
|
|
|
|
|
|
|
|
|||||||
В случае, когда частоты взаимно перпендикулярных колебаний |
||||||||||||||||
отличаются на очень малую величину |
Δω , их можно рассматривать как |
|||||||||||||||
колебания одинаковой частоты, но с медленно изменяющейся разностью |
||||||||||||||||
фаз. В самом деле, уравнения колебаний можно представить следующим |
||||||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = Acosωt |
|
|
|
|
|
|
|
|
|
||
|
|
|
y = Bcos ωt + Δωt + α , |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
где |
|
|
|
выражение |
|||
|
y |
|
A |
|
|
|
|
|
|
|
|
|
|
Δωt + α |
||
|
|
|
|
|
|
|
|
рассматривается |
|
как |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
разность |
фаз, |
медленно |
|||||
|
|
|
|
|
|
B |
|
|
изменяющуюся |
|
|
со |
||||
|
|
|
|
|
|
|
|
временем |
по |
линейному |
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x |
закону. |
|
|
|
|
|
|
||
|
O |
|
|
|
|
|
|
|
|
|
|
Результирующее |
||||
|
|
|
|
|
|
|
|
движение |
в |
этом |
случае |
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям
разности фаз от π до π .
Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу.
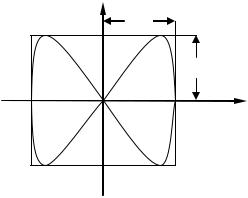
На рис.11 показана одна из простейших траекторий, получающаяся при отношении частот 1:2 и разности фаз / 2 . Чем ближе к единице
рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу.
Фигуры Лиссажу позволяют найти частоту одного из колебаний, если известна частота другого. Это обусловлено тем, что кратность частот легко находится с помощью секущих, параллельных координатным осям.
Затухающие колебания. Гармонический осциллятор при наличии сил
сопротивления
Как уже отмечалось, затухающие колебания возникают при наличии сил сопротивления (трения) и обусловлены рассеянием (диссипацией) энергии. Если убыль энергии не восполняется за счѐт работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем, наиболее часто встречающемся, случае сила сопротивления пропорциональна величине скорости:
F = r |
dx |
, |
(30) |
сопр |
dt |
|
где r - постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила сопротивления и скорость имеют противоположные направления, следовательно, их проекции на ось x
имеют разные знаки.
Запишем уравнение второго закона Ньютона для движения груза на пружине при наличии сил сопротивления:
m |
d 2 x |
= kx r |
dx |
. |
(31) |
dt 2 |
|
||||
|
|
dt |
|
||
Введя обозначения: 2β = r / m,ω2 = k / m , |
получим однородное |
||||
|
|
0 |
|
|
|
|
|
17 |
|
|
|
дифференциальное уравнение затухающих колебаний:
|
d 2 x |
+ 2β |
dx |
+ ω2 x = 0 , |
(32) |
|
|
|
|||
|
dt 2 |
|
dt |
0 |
|
|
|
|
|
||
где β - коэффициент затухания, ω0 |
- собственная частота колебаний, |
||||
т.е. частота, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при r 0 ).
Решение уравнения (32) проведем через анализ рассеяния энергии. Для этого сначала найдем полную энергию гармонического осциллятора при отсутствии сил сопротивления. Подставив в выражение
для кинетической энергии скорость осциллятора (3), получим: |
|
||||||||||||
|
m 2 |
|
|
|
mω2 |
A2sin 2 ω t + α |
|
|
|
|
|
||
Ek = |
|
|
= |
0 |
0 |
. |
|
(33) |
|
||||
2 |
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Потенциальная энергия упругой деформации после подстановки |
|||||||||||||
x из формулы (1) имеет следующий вид: |
|
|
|
|
|
||||||||
|
|
|
|
kx2 |
kA2 cos 2 ω t + α |
|
|
|
|||||
|
E p = |
|
|
|
|
= |
0 |
|
|
. |
(34) |
|
|
|
|
|
2 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Выразив из формулы |
ω2 = k / m коэффициент k = mω2 |
и |
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
подставив его в (34), получим выражение для полной энергии гармонического осциллятора:
E = Ek + E p |
= |
kA2 |
. |
(35) |
|
||||
|
2 |
|
|
|
Полная энергия гармонического осциллятора сохраняется в отсутствие сил сопротивления и пропорциональна квадрату амплитуды колебаний. Таким образом, процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние (за период колебаний) значения потенциальной и кинетической энергии
одинаковы, и каждое из них равно E / 2 .
Выясним, как влияют силы сопротивления на энергию колебательной системы (осциллятора). Будем при этом считать, что сила сопротивления настолько мала, что вызываемые ею потери энергии за один период относительно малы. Потеря энергии телом определится как
работа, произведѐнная силой сопротивления. За время dt эта работа, а с ней и потеря энергии dE равна произведению силы сопротивления
18
|
= r |
dx |
|
Fсопр |
|
на смещение тела ( dx dt ): |
|
|
|||
|
|
dt |
|
dE = F dx = r |
dx |
dt = r 2 dt , |
||||||||
|
|
|
||||||||
|
|
сопр |
|
|
|
dt |
|
|||
|
|
|
|
|
|
|
||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
dE |
= r 2 |
= |
2r m 2 |
|
|||||
|
|
|
|
|
|
. |
(36) |
|||
|
dt |
m |
2 |
|||||||
|
|
|
|
|
||||||
При сделанном нами предположении о малости сил |
||||||||||
сопротивления мы можем |
в (36) |
|
|
заменить |
кинетическую энергию |
|||||
половиной полной энергии осциллятора E :
dE |
= 2βE . |
(37) |
|
dt |
|||
|
|
Перепишем это выражение в виде:
|
dE |
= d lnE = 2βdt . |
||
|
E |
|||
|
|
|
|
|
Путем интегрирования находим, что |
|
|||
окончательно: |
|
|
|
|
E = E |
e 2 βt , |
(38) |
||
|
|
0 |
|
|
x
|
|
A e t |
|
A0 x |
|
0 |
|
0 |
t |
||
|
|||
|
|
T
Рис. 12
lnE = 2βt + const ,
где E0 – значение
энергии в начальный момент времени
( t 0 ).
Таким образом, энергия колебательной системы убывает изза сил сопротивления по экспоненциальному закону. Вместе с энергией убывает и амплитуда колебаний. Поскольку энергия
19

пропорциональна квадрату амплитуды, получаем
|
|
A = A e βt |
. |
|
(39) |
|
|
0 |
|
|
|
Таким образом, при не слишком большом затухании общее |
|||||
решение уравнения (32) имеет вид: |
|
||||
|
x = A e βt cos ωt +α |
. |
(40) |
||
|
0 |
|
|
|
|
Здесь A0 – значение амплитуды в начальный момент времени, α - начальная фаза, ω - частота колебаний.
|
|
|
|
|
|
ω = ω2 |
β 2 |
. |
(41) |
||
0 |
|
|
|
|
|
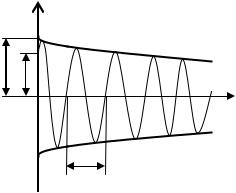
На рисунке 12 дан график функции (40). Пунктирными линиями показаны пределы, в которых находится смещение x колеблющейся точки. В
соответствии с видом функции (40) движение системы можно рассматри-
вать как гармоническое колебание частоты ω с амплитудой,
изменяющейся по закону, определяемому формулой (39). Верхняя из пунктирных кривых на рисунке 12 дает график функции A(t). Начальное
смещение x0 зависит кроме A0 также от начальной фазы α :
x0 = A0cosα .
Степень убывания амплитуды определяется коэффициентом затухания. За время 1/ амплитуда уменьшается в e раз - это
время называется временем релаксации колебаний. Сделанное нами выше предположение о малости сил сопротивления означает, что
предполагается большим по сравнению с периодом колебаний
|
T = |
|
2π |
= |
|
|
2π |
|
|
, (42) |
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
ω |
|
|
ω02 |
β 2 |
|
||||||
т.е. |
за время релаксации |
происходит большое число колебаний |
|||||||||||||
Ne |
/ T . Величину, |
|
|
обратную Ne |
называют |
логарифмическим |
|||||||||
декрементом затухания : |
|
|
|
A t |
|
||||||||||
|
= |
|
1 |
= T = ln |
|
||||||||||
|
|
|
|
. |
(43) |
||||||||||
|
N |
|
A t +T |
||||||||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
||
Итак, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за время релаксации. Кроме того, логарифмический декремент затухания часто определяют как
20
