
- •Розділ 1. Загальні відомості щодо науки, наукових досліджень, кадрів та установ
- •Тема 1 Наука як система знань.
- •Тема 2. Наукові дослідження.
- •Тема 3. Організація наукових досліджень.
- •Тема 4. Методологія наукових досліджень.
- •Розділ 2. Методи теоретичних досліджень
- •Тема 5. Аналітичні методи досліджень.
- •Тема 6. Аналітично-експериментальні методи досліджень.
- •Тема 7. Ймовірносно - статистичні методи
- •Тема 8. Методи системного аналізу.
- •Розділ 3. Методика експериментальних досліджень
- •Тема 9. Методологія та види експерименту.
- •Тема 10. Оцінка характеристик змінних об’єкту.
- •Тема 11. Кореляційний аналіз дослідних даних.
- •Тема 12. Апроксимація дослідних даних.
- •Розділ 4. Постановка та проведення основного експерименту.
- •Тема 13. Плани експерименту першого порядку.
- •Тема 14. Обробка результатів експерименту за планами першого порядку.
- •Тема 15. Плани експерименту другого порядку.
- •Тема 16. Обробка результатів експерименту за планами другого порядку.
- •Література
Тема 11. Кореляційний аналіз дослідних даних.
Вибірковий коефіцієнт кореляції та методика оцінки його значимості. Відсіювання незначущих факторів
Кореляційний аналіз є складовою частиною математичного апарату обробки експериментальних даних. За його допомогою оцінюють зв’язок між змінними, відсіюють зв’язки, що є незначущими, або несуттєві фактори.
Вибірковий
коефіцієнт кореляції
визначають за формулою:
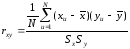 , де N – кількість дослідів;
, де N – кількість дослідів;
 - оцінки математичного сподівання
змінних х
та у;
Sx ,
Sy –
оцінки середньоквадратичних відхилень
цих змінних.
- оцінки математичного сподівання
змінних х
та у;
Sx ,
Sy –
оцінки середньоквадратичних відхилень
цих змінних.
Для
перевірки значимості коефіцієнту
кореляції використовують критерій
Стьюдента, тобто, знаходять його
розрахункове значення tр
і порівнюють з табличним tт
. Розрахунковий t – критерій: tр
=
 .
.
Табличне значення tт знаходять для числа ступенів свободи f = N – 2 і рівня значимості q = 0,05 (або заданого). У разі виконання умови: tр > tт лінійний зв’язок між х і у існує.
Приклад.
В результаті досліджень впливу питомої
витрати пари на розпил мазуту в форсунки
(х1,
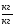 )
і продуктивності обертової печі для
обпалу вапняку (х2,
)
і продуктивності обертової печі для
обпалу вапняку (х2,
 )
на питому витрату палива (у,
)
на питому витрату палива (у,
 )
отримані дані, які наведені в табл.
Знайти коефіцієнти кореляції між
факторами х1
, х2
та змінною у,
а також оцінити їх значимість.
)
отримані дані, які наведені в табл.
Знайти коефіцієнти кореляції між
факторами х1
, х2
та змінною у,
а також оцінити їх значимість.
|
№№ дослідів |
х1 |
х2 |
У |
|
1 |
0,69 |
29 |
50,5 |
|
2 |
0,66 |
91 |
30,9 |
|
3 |
0,45 |
82 |
37,4 |
|
4 |
0,49 |
99 |
37,8 |
|
5 |
0,48 |
148 |
19,7 |
|
6 |
0,48 |
165 |
15,5 |
|
7 |
0,41 |
133 |
49,0 |
|
Σ |
3,66 |
747 |
240,8 |
Рішення. З даних таблиці знаходимо:
-
середні значення параметрів
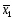 = 0,523;
= 0,523;
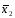 = 106,71;
= 106,71;
 = 34,4;
= 34,4;
- їх середньоквадратичні відхилення Sx1 = 0,1076; Sx2 = 46,096; Sу = 13,407;
- вибіркові коефіцієнти кореляції rx1 x2 = - 0,585; rx2 у = - 0,605; rx1 у = + 0,166;
- розрахункові значення критерію Стьюдента tp1 = 1,61; tp2 = 0,38; tp3 = 1,70.
Табличне значення t - критерію для числа ступенів свободи f = 7 – 2 =5 і рівня значимості q = 0,05 складає tт = 2,37. Оскільки для всіх випадків tpі < tт (і = 1, 2, 3), з імовірністю 95% можна зробити висновок, що лінійного зв’язку між змінними немає.
Тема 12. Апроксимація дослідних даних.
Передумови регресійного аналізу. Рівняння лінійної вибіркової регресії; визначення коефіцієнту регресії та його значимості. Множинна регресія; коефіцієнти часткової регресії та оцінка їх значимості. Методики розробки криволінійних регресійних моделей.
Шляхом апроксимації результатів експерименту можуть бути отримані різні функціональні залежності – поліноміальні, ступеневі, логарифмічні і т. д.
Основним математичним апаратом для отримання апроксимаційних моделей є метод найменших квадратів. Регресивний аналіз звичайно проводять за результатами пасивного або неспланованого активного експерименту. Основними передумовами регресивного аналізу є наступні.
1. Вихідна змінна об’єкту дослідження є випадковою величиною з нормальним законом розподілу;
2. Кореляція між вхідними змінними відсутня;
3. Дисперсія вихідної змінної не залежить від її абсолютної величини, тобто, дисперсії вихідної змінної є однорідними в будь – який точці факторного простору;
4. Об’єкт дослідження позбавлений динамічних властивостей.
Рівняння
лінійної вибіркової регресії
має вигляд:
 =
вх, де
=
вх, де
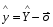 - відхилення розрахункового значення
вихідного параметра
- відхилення розрахункового значення
вихідного параметра
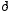 від середнього за вибіркою
від середнього за вибіркою
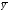 ;
;
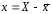 - відхилення вхідної змінної Х від її
середнього вибіркового значення
- відхилення вхідної змінної Х від її
середнього вибіркового значення
 ;
в –
вибірковий коефіцієнт регресії, який
визначають за формулою:
;
в –
вибірковий коефіцієнт регресії, який
визначають за формулою:
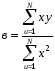 ,
,
де
 - відхилення вибіркового значення
вихідного параметру У від середнього
- відхилення вибіркового значення
вихідного параметру У від середнього
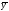 ;
N – кількість дослідів (спостережень,
вимірів).
;
N – кількість дослідів (спостережень,
вимірів).
Тобто,
рівняння регресії можна записати у
вигляді:

Для
оцінки ступеня згоди лінії регресії з
дослідними даними визначають відхилення
від регресії dху
=
 .
Величина
.
Величина
 є основою для оцінки помилки, яка виникає
при виборі лінії регресії. Оскільки в
розрахунку використовуються дві середні
величини (
є основою для оцінки помилки, яка виникає
при виборі лінії регресії. Оскільки в
розрахунку використовуються дві середні
величини (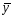 та
та
 ),
то число ступенів свободи дорівнює (N –
2). Тоді середній квадрат відхилень від
регресії і вибіркове стандартне
відхилення коефіцієнту регресії:
),
то число ступенів свободи дорівнює (N –
2). Тоді середній квадрат відхилень від
регресії і вибіркове стандартне
відхилення коефіцієнту регресії:
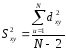 ;
;
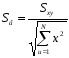 .
.
Критерій
суттєвості для коефіцієнту в
визначають за формулою: tp
=
 та порівнюють його з табличним значенням
t – критерію для числа ступенів свободи
f = N –2 і заданого рівня значимості q. За
умови tp
≥ tт
коефіцієнт в
є значимим.
та порівнюють його з табличним значенням
t – критерію для числа ступенів свободи
f = N –2 і заданого рівня значимості q. За
умови tp
≥ tт
коефіцієнт в
є значимим.
Приклад.
Досліджувався вплив продуктивності
агрегату Х,
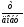 на викиди пилу з нього У,
на викиди пилу з нього У,
 ;
результати вимірів наведені в табл.
Знайти залежність між цими параметрами
у вигляді лінійної функції.
;
результати вимірів наведені в табл.
Знайти залежність між цими параметрами
у вигляді лінійної функції.
|
№№ вимірів |
1 |
2 |
3 |
4 |
5 |
|
Х |
35 |
45 |
55 |
65 |
75 |
|
У |
114 |
124 |
143 |
158 |
166 |
Рішення. Середні значення параметрів:
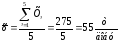 ;
;
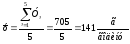 .
.
Результати проміжних розрахунків зводимо в табл.
|
№ |
Х -
|
У -
|
(Х - |
(У - |
(Х- |
|
|
(У- |
|
1 |
- 20 |
- 27 |
400 |
729 |
540 |
113,4 |
0,6 |
0,36 |
|
2 |
- 10 |
- 17 |
100 |
289 |
170 |
127,2 |
- 3,2 |
10,24 |
|
3 |
0 |
2 |
0 |
4 |
0 |
141,0 |
2,0 |
4,0 |
|
4 |
10 |
17 |
100 |
289 |
170 |
154,8 |
3,2 |
10,24 |
|
5 |
20 |
25 |
400 |
625 |
500 |
168,6 |
- 2,6 |
6,76 |
|
Σ |
0 |
0 |
1000 |
1936 |
1380 |
|
0 |
31,60 |
Вибірковий
коефіцієнт регресії:
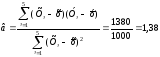 .
.
В початкових одиницях рівняння регресії має вигляд:
 -
-
 = в(Х -
= в(Х -
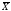 );
);
 -
141 = 1,38(Х - 55);
-
141 = 1,38(Х - 55);
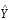 = 65,1 + 1,38Х,
= 65,1 + 1,38Х,
 .
.
Для
оцінки ступеня згоди лінії регресії з
даними вимірів визначаємо
 ,
(У -
,
(У - ),
(У -
),
(У -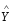 )2,
значення яких наведені в табл., число
ступенів свободи f = 5 – 2 = 3, середній
квадрат відхилень і стандартне відхилення
від регресії:
)2,
значення яких наведені в табл., число
ступенів свободи f = 5 – 2 = 3, середній
квадрат відхилень і стандартне відхилення
від регресії:
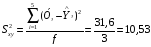 ;
Sxy =
3,24.
;
Sxy =
3,24.
Вибіркове стандартне відхилення коефіцієнта регресії та розрахунковий критерій Стьюдента для нього:
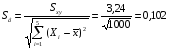 ;
;
 .
.
Табличний критерій Стьюдента для f = 3 i q = 5% складає tт = 3,18, що значно перевищує розрахункову величину. Тому коефіцієнт регресії є значимим.
Рівняння множинної регресії має вигляд:
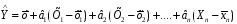 ,
,
де в1 , в2 ,…, вn – коефіцієнти часткової регресії, які визначають за методом найменших квадратів з системи нормальних рівнянь. Для двох вхідних факторів об’єкту вона має вигляд:
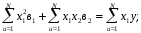
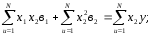
Рішення цієї системи відносно коефіцієнтів часткової регресії:


Перевірку значимості коефіцієнтів часткової регресії виконують аналогічно за веденою вище методикою.
Збільшення
числа змінних призводить лише до
ускладнення обчислювання. Наприклад,
для трьох незалежних змінних Х1,
Х2,
Х3 і
однієї залежної У рівняння регресії
має вигляд:
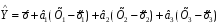 і коефіцієнти регресії
визначають з системи рівнянь:
і коефіцієнти регресії
визначають з системи рівнянь:
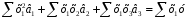 ;
;
 ;
;
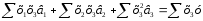 .
.
Для створення криволінійної регресивної моделі використовують два підходи. При першому будують графіки дослідних даних спочатку з застосуванням рівномірних шкал по осях координат. Якщо на графіку не отримана лінійна залежність, починають послідовно вибирати функціональні шкали по одній або по двох осях координат. Для цього використовують логарифмічні шкали. Наприклад, якщо має місце експонентна залежність вигляду: W = ABХ, то шляхом логарифмування цього рівняння можна отримати рівняння прямої лінії:
LnW = lnA + ХlnB або У = а + вХ.
Цей
спосіб використання логарифму замість
самої величини називають способом
спрямлення. Інколи для
спрямлення використовують інші функції,
наприклад,
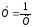 ;
;
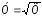 і т. д.
і т. д.
Другий підхід полягає у використанні полінома другого порядку:
У = а + вХ + сХ2.
Тут
замість спрямлення даних виконується
додавання третьої змінної – квадрату
Х. Тим самим задача зводиться до
використання множинної регресії. Процес
обчислення є однаковим, але тут в якості
незалежних змінних фігурують Х та Х2.
Замість Х2
можуть бути взяті
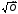 ,
lnX,
,
lnX,
 і т. д.
і т. д.



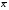 )2
)2 )2
)2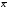 )*
(У -
)*
(У -
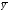 )
)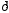

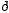 )2
)2