Тема 10. Оцінка характеристик змінних об’єкту.

Оцінка математичного очікування, дисперсії; їх довірчі інтервали. Визначення відмінності середнього вибіркового від стандартного. Перевірка відмінності дисперсій. Виявлення та виключення аномальних значень з вибірки. Визначення необхідної повторності дослідів.

Оцінки математичного сподівання та дисперсії для дискретної випадкової величини визначаються за формулами:

; .

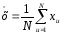Знаменник вибіркової дисперсії дорівнює різниці між об’ємом вибірки N та числом зв’язків, які накладені на цю вибірку (кількість середніх величин). Цю різницю f називають числом ступенів свободи вибірки.

Для визначення точності оцінки величини а_N користуються довірчими інтервалами а_N ± ε, а для визначення надійності – довірчою надійністю Р_ε = Р(а_N – ε < а < а_N + ε), тобто невідоме значення параметру а з імовірністю Р_ε знаходиться в довірчому інтервалі а_N ± ε. В технічних розрахунках звичайно приймають Р_ε = 0,95 (95%).

Розрахунок інтервальних оцінок для математичного сподівання та дисперсії змінної Х виконується за формулами:

; ,

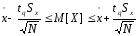де S_х – середньоквадратичне відхилення; t_q – значення критерію Стьюдента (псевдонім англійського математика В. С. Госета), який знаходять з таблиць для f = N – 1 і рівня значимості q при певній довірчий імовірності Р; оскільки звичайно Р = 0,95, тому q = 0,05 (5%), якщо це не обговорено спеціально для конкретних досліджень; 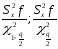- значення χ² – розподілу Пірсона для рівня значимості 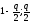відповідно.

Приклад. В результаті 8 – міразового контролю складу продуктів згоряння на виході з агрегату отримано, що вміст оксидів азоту в них становить: 76,48; 76,43; 77,20; 76,45; 76,25; 76,48; 76,48; 76,60 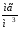. Визначити інтервальні оцінки дисперсії та математичного сподівання.

Рішення. Оцінки математичного сподівання та дисперсії:

; .

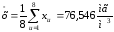З таблиці розподілу Стьюдента для f = 8 – 1 = 7; q = 5% знаходимо t_q = 2,36; тоді інтервальна оцінка математичного сподівання:

; .

Для f = 7 з таблиці розподілу Пірсона знаходимо ; ; 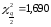тоді інтервальна оцінка дисперсії:

; .

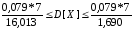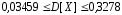Перевірку гіпотези щодо відмінності середнього обчисленого від стандартного виконують за співвідношенням: 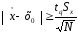. Різниця між стандартним значенням х₀ і середнім вибірковим 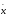є суттєвим при виконанні цього співвідношення.

Приклад. Температура в агрегаті, яку вимірювали еталонним термометром, складає х₀ = 1000⁰С. При вимірах її за допомогою інших термометрів отримані значення: 986; 1005; 991; 994; 983; 1002; 996; 998; 1002; 983⁰С. Чи суттєво відрізняється середнє значення вимірів цими термометрами від еталонного?

Рішення. Розрахуємо оцінки математичного сподівання, дисперсії та середньоквадратичного відхилення: ; ; .

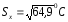Критерій Стьюдента для числа ступенів свободи f = 10 –1 = 9 і рівня значимості q = 5% знаходимо з таблиць: t_q = 2,23. Тоді маємо:

> .

Тобто, середнє значення вимірів суттєво відрізняється від стандартного.

Різні серії дослідів можуть бути виконані з різною якістю, тому виконують перевірку відмінності дисперсій в цих серіях. Припустимо, що маємо дві вибірки об’ємом N₁ та N₂, для яких визначені оцінки дисперсій S₁² та S₂². Ці дисперсії є однаковими, якщо виконується умова: , де S₁² > S₂² ; F – критерій Фішера для числа ступенів свободи f₁ i f₂ та заданого рівня значимості q_задане.

Приклад. Порівняти точність аналізів вмісту кисню в продуктах згоряння, які виконані двома лаборантами. Лаборант А виконав 20 аналізів з результатами: 4,40; 4,56; 4,42; 4,59; 4,55; 4,45; 4,55; 4,39; 4,75; 4,72; 4,53; 4,66; 4,90; 4,50; 4,45; 4,66; 4,80; 4,36; 4,75; 4,22. Результати 13 аналізів лаборанта В: 4,42; 4,47; 4,70; 4,72; 4,53; 4,55; 4,60; 4,64; 4,29; 4,52; 4,57; 4,56; 4,66. Різницю точності аналізів визначити для 5% - ного рівня значимості.

Рішення. Розраховуємо оцінки математичного сподівання та дисперсії для кожної серії дослідів. Лаборант А:

; .

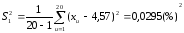Лаборант В: ; ;

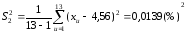S₁² = 0,0295 > S₂² = 0,0139.

Середні значення аналізів у обох лаборантів приблизно рівні, однак розсіювання результатів біля середніх значень є різним. Табличне значення критерію Фішера для f₁ = 20 – 1 = 19; f₂ = 13 – 1 = 12; q = 5% складає F = 2,50. Оскільки , то з імовірністю Р_ε = 95% можна стверджувати, що різниця в точності аналізів лаборантів А і В є несуттєвою.

В об’ємі вибірки можуть зустрічатися різко відмінні значення, які ще називають аномальними. Виявлення та виключення аномальних значень з вибірки здійснюється за наступною процедурою.

Спочатку знаходять максимальне відхилення від середнього:

Δ_max = x_max(min) - , де x_max(min) – аномальне значення в виборці.

Потім виконується оцінка: │Δ_max │ > сS_x , де с – величина, яку знаходять зі співвідношення шляхом ітерацій.

Значення x_max(min) відкидається, якщо виконується наведена нерівність.

Приклад. За даними аналізу продуктів згоряння отриманий вміст СО₂ в них: х₁ = 23,2; х₂ = 23,4; х₃ = 23,5; х₄ = 24,1; х₅ = 25,5%. Чи є значення х₅ аномальним і чи слід виключити його з вибірки?

Рішення. Обчислюємо оцінку математичного сподівання і максимальне відхилення у виборці: ; Δ_max =│25,5 – 23,55│ = 1,95%.

Оцінка дисперсії по залишку вибірки ( по чотирьом вимірам):

S_x² = ; S_x = 0,67.

Табличне значення t – критерію для q = 5%; N = 5; f = 5 – 1 = 4 складає t_q = 2,776. Зі співвідношення: методом ітерацій отримуємо: с = 1,67. Тоді припустиме відхилення: СS_x = 1,67*0,67 = 1,12%.

Оскільки Δ_max > сS_x , то значення х₅ повинно бути виключено з вибірки.

Важливим практичним питанням, яке вирішується на стадії попереднього експерименту, є визначення необхідної повторності дослідів. Мінімально потрібна кількість паралельних дослідів визначається за наступною процедурою.

Для масиву дослідних даних попередніх N вимірів визначають середнє значення та середньоквадратичне відхилення:

; .

Потім знаходять гранично припустиме відхилення параметру від середнього для заданого рівня значимості q = 0,05: Δ_гр = q.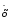

Критерій Стьюдента t_0,05 для числа ступенів свободи f = N – 1 та рівня значимості q = 0,05 знаходять за допомогою таблиць і визначають різницю між стандартним середнім та обчисленим за вибіркою для даної кількості вимірів N:

δ =

Якщо δ < δ_гр , зменшують N, знаходять для нового N значення t_0,05 з таблиць і знову розраховують δ, поки δ не стане більшим за δ_гр . Найменше значення N, коли забезпечується умова δ < δ_гр , приймають за потрібну кількість паралельних вимірів (дослідів).

Приклад. Попередні N = 12 вимірів показали, відрив факелу при стабільних інших параметрах спостерігався при витраті палива на пальник х_u, 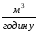: 105; 100; 100; 100; 102,5; 100; 97,5; 97,5; 102,5; 105; 102,5. Визначити необхідну повторність дослідів при дослідженні процесу стабілізації полум’я.

Рішення. Середня витрата палива та середньоквадратичне відхилення за результатами N = 12 дослідів: = 101,25 ; S_x = 2,5 .

Гранично припустиме відхилення параметру від середнього при q = 0,05:

δ_гр = q = 101,25*0,05 = 5,063

Табличне значення t – критерію для f = N –1 = 12 – 1 = 11 і довірчої імовірності Р_ε = 95% з таблиць t_0,05 = 2,2.

Різниця між стандартним середнім та обчисленим за вибіркою:

δ = .

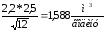Отримане значення δ значно менш, ніж δ_гр, тому розрахуємо δ для менших значень N. Для N = 6 значення t – критерію t_0,05 = 2,57 і δ = 2,623; для N = 4 t_0,05 = 3,38 і δ = 3,975; для N = 3 t_0,05 = 4,30 і δ = 6,207, що більш, ніж δ_гр. Відповідно, приймаємо чотириразову повторність вимірів.

Ще однією задачею попереднього експерименту є визначення закону розподілу випадкової величини. Звичайно перевіряють його нормальність, оскільки цей розподіл є домінуючим. Для цього будують гістограму. На вісі абсцис відкладають інтервали, які відповідають групам сукупності випадкової величини, і на кожному з них, як на основі, будують прямокутник. Височина його дорівнює частоті даної групи 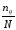, де n_g – кількість вимірів в групі; N – загальна кількість вимірів, тобто об’єм вибірки.

Кількість груп вибирають таким чином, щоб результати вимірів були добре оглядові і утримували велику кількість відомостей. Алгоритм побудови гістограми наступний.

1. Діапазон зміни випадкової величини у виборці х_min x_max ділять на ε інтервалів; ε вибирають за емпіричною формулою: ε = 1 + 3,2ln N .

Довжину інтервалів приймають однаковою: Δg = .

2. Визначають число n_g (g = 1, 2, …, ε) елементів вибірки, які знаходяться в кожному інтервалі Δg , і відносну частоту попадання випадкової величини у відповідний інтервал: Р_g = .

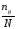3. Отриманий варіаційний ряд записують в таблицю, причому елементам вибірки, які потрапили в g – тий інтервал, приписують середнє значення: 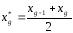і будують гістограму Р_g → х_g-1 x_g.

Після побудови гістограми виконують перевірку нормальності закону розподілу вибірки за допомогою критеріїв згоди, які оцінюють розбіжності між теоретичними та емпіричними розподілами. Звичайно для цього використовують критерій згоди Пірсона.