Розділ 2. Методи теоретичних досліджень

Тема 5. Аналітичні методи досліджень.

Використання елементарних функцій та звичайних диференційних рівнянь. Дослідження за допомогою диференційних рівнянь у часткових похідних. Умови однозначності. Операційне перетворення. Наближені числові методи.

Математичні методи аналізу можна умовно розділити на 4 групи.

1. Аналітичні методи досліджень, в яких використовують апарат елементарної математики, диференційного і інтегрального обчислення, інших розділів вищої математики для вивчення неперервних детермінованих процесів.

2. Методи математичного аналізу з використанням експерименту. Це метод аналогій, теорія подібностей, метод розмірностей.

3. Ймовірносно – статистичні методи, які використовують для вивчення дискретних і неперервних випадкових процесів. Це апарат математичної статистики, дисперсійного і кореляційного аналізу, теорія надійності та ін.

4. Методи системного аналізу для дослідження складних систем з різноманітними взаємозв’язками елементів, які працюють безперервно і дискретно, детерміновано і випадковим чином. Це методи дослідження операцій, теорія масового обслуговування, теорія управління, теорія множин та ін.

За допомогою аналітичних методів встановлюють математичні залежності між параметрами об’єкту, що вивчається, які потім використовують для аналізу їх впливу на функціонування цього об’єкта. Основу побудови математичних моделей складає ідеалізація реальної системи або об’єкту. Ідеалізація полягає у виділенні визначальних і відкиданні другорядних в умовах даної задачі властивостей явища, процесу, об’єкту і складанні на цій основі рівнянь і нерівностей їх протікання або функціонування.

Елементарні функції використовують у випадках, коли треба спростити модель і отримати наближене рішення задачі. Часто застосовують лінійні, експоненціальні, параболічні, показові функції; для вивчення коливальних процесів – тригонометричні. Неперервність цих функцій дозволяє диференціювати їх і інтегрувати, визначати найкращі або найгірші умови здійснення процесу або функціонування об’єкту шляхом знаходження екстремумів і їх дослідження.

Прикладом може служити параболічна залежність ККД теплового агрегату від його продуктивності у вигляді: η=а₀+а₁Р-а₂Р² , або питомої витрати теплоти від продуктивності: в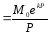, де а₀, а₁, а₂, к – деякі коефіцієнти, які визначають за експериментальними даними на агрегаті; М₀ - потужність холостого ходу.

Шляхом диференціювання цих виразів легко знайти, що максимум ККД досягається при Р*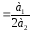, а мінімум питомої витрати теплоти – при Р^*.

Звичайні диференційні рівняння використовують для теоретичного аналізу функції тільки однієї змінної. Рівняння першого порядку має вигляд:

; .

Рівняння вищих порядків: .

Загальне рішення подібних рівеь являє собою родину кривих на площині виду: F(x, y, c₁, c₂, …, c_n), де с_1, с₂, … ,с_n – постійні інтегрування .

Ці постійні визначають шляхом завдання початкових умов, тобто, значень функції F в деяких відомих точках х та у, і таким чином знаходять часткові рішення диференційного рівняння.

Звичайні диференційні рівняння використовують для аналізу простих і середніх за складністю процесів, наприклад:

-нагрівання термічно тонкого тіла: де в лівій частині вказано зростання ентальпії тіла, а в правій –надходження енергії ззовні через поверхню F за одиницю часу.

-процес ідеального змішування: ;

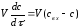-реакція крекінгу нафтової сировини: де х – частка перетвореної сировини; а – кількість вихідної сировини; к – константа швидкості реакції; - швидкість розкладу індивідуальних вуглеводнів;

-процес розчину речовини (цукру, солі, цементу і т.д.): 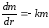, де m – кількість нерозчиненої речовини; к – коефіцієнт пропорційності.

За останнім рівнянням швидкість розчинення є пропорційною кількості нерозчиненої речовини і з часом процес розчинення згасає. В цьому можна переконатися з рішення диференційного рівняння:

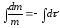; ln m = - k+ c₁; m=c₂е^-k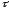

Сталу інтегрування знаходимо з початкових умов: при τ=0 початкова кількість нерозчиненої речовини m=m₀. Тоді маємо: m₀=C₂=m₀ і кінцево отримуємо:

m=m₀e^-k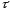

Швидкість згасання процесу розчину залежить від значення коефіцієнту к, якій визначається природою речовини і температурою розчину.

Диференційні рівняння в часткових похідних мають, наприклад, вигляд:

.

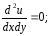
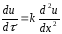Їх використовують, зокрема, для аналізу процесів течії рідини і газу, дифузії, теплових, коливальних процесів і т.д. Загальне рішення цих рівнянь залежить не від довільних постійних, а від довільних функцій, і являє собою функції декількох незалежних змінних. Сутність задачі полягає у встановленні залежності u = f(x, y, τ, …) між функцією u і незалежними x, y, τ, …, яка задовольняє диференційному рівнянню і додатковим умовам задачі. Ці додаткові умови називають умовами однозначності; вони визначаються фізичним смислом задачі і чітко виділяють явище, що вивчається, з цілого класу явищ, який описує дане диференційне рівняння в часткових похідних. Ознаками умов однозначності є наступні:

- геометрія об’єкту, системи, тобто форма і розміри тіла;

- фізичні властивості об’єкту ( теплопровідність, в’язкість, теплоємність, густина, пружність і т. д. );

- початкові умови, тобто стан об’єкту, системи в початковий момент часу;

- граничні умови, тобто умови взаємодії об’єкту на границях з оточуючим середовищем.

Початкові та граничні умови ще називають крайовими.

Прикладом диференційного рівняння в часткових похідних є рівняння теплопровідності: 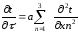, де а – коефіцієнт температуропроводності.

За цім рівнянням температура тіла t в будь-якій точці при нагріванні або охолодженні є функцією часу τ і координат х₁, х₂, х₃. Для одномірного температурного поля воно буде мати вигляд: .

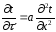Ефективним засобом рішення задач тепло - та масообміну є використання методів операційного перетворення Фур’є, Лапласа, Беселя, Карсона – Хевісайда. Сутність цих перетворень полягає в перетворенні функції f(τ) змінної τ, яку називають початковою або оригіналом, в функцію f^*(Р) іншої змінної Р, яку називають відображенням. При цьому аналізують не саму функцію – оригінал, а її змінене значення – відображення. Це дозволяє замінювати складні операції диференціювання і інтегрування функції – оригіналу f(τ) більш простими алгебраїчними операціями з відображенням f^*(Р). Після виконання цих операцій виконують зворотній перехід від f^*(P) до f(τ).

Перетворення здійснюються шляхом множення початкової функції на іншу і її інтегрування. Так, перетворення Лапласа має вигляд: f^*(P)=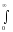e^-Pτ f(τ) dτ , де Р = С + іω – комплексне число. Перетворення Фур’є здійснюється за виразом:

f^*(іω)=e^{- іωτ} f(τ) dτ .

Перетворення Карсона – Хевісайда часто застосовують для рішення задач з електротехніки і воно відрізняється від перетворення Лапласа додатковим множенням на оператор Р: f^*(P)= Р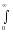e^-Pτ f(τ) dτ .

Зворотній перехід від відображення до оригіналу для наведених перетворень здійснюється відповідно за формулами:

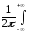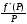f(τ)=f^*(P) e^Pτ dP; f(τ)=f^*(іω) e^іωτ dω; f(τ)= dP.

Для інтегральних рівнянь не існує загального методу точного рішення. Застосовують методи послідовних наближень, варіаційного обчислення, функції комплексної змінної та інші. Однак аналітичні методи, як правило, дозволяють знайти рішення лише відносно простих задач. В більш складних випадках використовують наближені числові методи, одним з яких є метод кінцевих різниць або сіток. Сутність цього методу полягає в заміні безкінечно малих диференціалів функції та аргументів в диференційному рівнянні та крайових умовах на малі, але кінцеві їх прирощення. Область пошуку рішення при цьому розбивають на однакові комірки – квадратні, прямокутні, трикутні або інші; задане диференційне рівняння замінюють в вузлах побудованої сітки відповідним кінцево – різницевим рівнянням; на основі граничних умов встановлюють значення рішення в граничних вузлах області пошуку. Зі складеної системи кінцево – різницевих рівнянь визначають величину функції в вузлах сітки, тобто отримують кількісне рішення задачі.