3. Применение метода искусственного базиса для решения задач линейного программирования

(М-ЗАДАЧА)

1. Постановка и методика решения м-задачи

Симплекс-метод удобно применять, когда все ограничения ЗЛП содержат неравенства ≤. В этом случае дополнительные переменные образуют базис и исходный опорный план очевиден. В противном случае, когда в ЗЛП встречаются разные типы ограничений ≤, =, ≥ применяют метод искусственного базиса.

Он состоит в следующем. В рассмотрение вводится т искусственных переменных x_n+1, x_n+2, … , x_n+m и решается расширенная задача (М-задача). Она заключается в нахождении минимума целевой функции

z = c₁x₁ + c₂x₂ + … + c_nx_n + Mx_n+1 + Mx_n+2 + … + Mx_n+m

при условиях

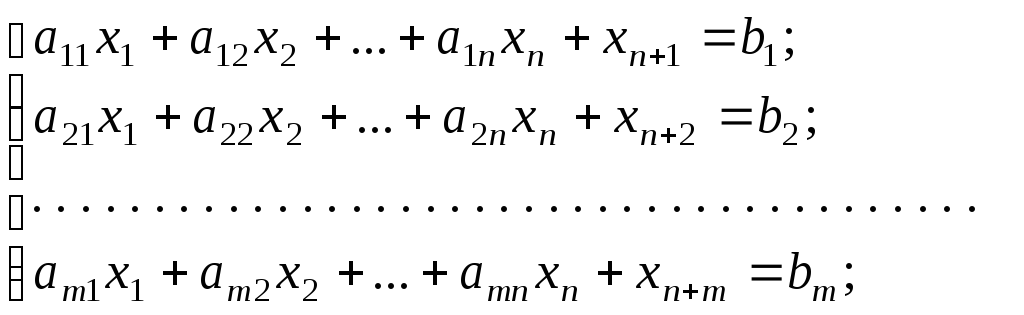
x_j  0, j = 1, 2,…, n, n + 1, …, n + m,

где М – любое большое положительное число.

Искусственные переменные могут быть приняты в качестве базисных переменных.

Для решения М-задачи составляют симплексную таблицу, отличающуюся от обычной наличием (m+2)-й строки (таблица 1). В этой строке находятся суммы соответствующих коэффициентов при свободных переменных в строках, соответствующих искусственным переменным.

Если задача решается на нахождение максимума, то в целевой функции полагают коэффициенты при искусственных переменных достаточно большими по абсолютной величине отрицательными числами. Поэтому в данном случае в целевую функцию искусственные переменные входят с коэффициентом «–М». При этом (m+2)-ю строку симплексной таблицы записывают суммы соответствующих коэффициентов при свободных переменных в строках, соответствующих искусственным переменным, взятые с противоположным знаком.

Таблица 1

Базисные переменные	Свободные члены	Свободные переменные				Симплексные отношения
		x1	x2	…	xn
xn+1	b1	a11	a12	…	a1n
xn+2	b2	a21	a22	…	a2n
…	…	…	…	…	…
xn+m	bm	am1	am2	…	amn
(m+1)-я строка	0	–с1	–с2	…	–сn
(m+2)-я строка				…

По (m+2)-й строке, содержащей наибольший положительный элемент, определяют разрешающий столбец. Выбор разрешающей строки и пересчет симплексной таблицы осуществляется как обычно. Искусственные переменные вытесняются из базиса и более не пересчитываются.

Итерационный процесс по (m+2)-й строке проводят до полного исключения искусственных переменных. При этом все элементы (m+2)-й строки будут равны нулю. Далее для решения используют обычный симплексный метод с выбором разрешающего столбца по элементам (m+1)-й строки.

Если при решении М-задачи оказалось, что в (m+2)-й строке нет положительных элементов, но не все искусственные переменные вытеснены из базиса, то система ограничений исходной задачи несовместна.