1.2. Алгоритм решения задачи линейного программирования графическим методом

Такой алгоритм предполагает выполнение следующих действий.

1. Записать уравнения граничных прямых.

2. Построить графики граничных прямых на плоскости.

3. Выделить область решения каждого неравенства системы.

4. Выделить область допустимых решений.

5. Построить градиент целевой функции.

6. Построить линию уровня.

7. Определить экстремальную точку области допустимых решений.

8. Вычислить значение целевой функции в экстремальной точке.

3. . Типовой пример

Пусть дана следующая задача.

Найти максимум целевой функции

z = 2x₁ + 2x₂

при ограничениях

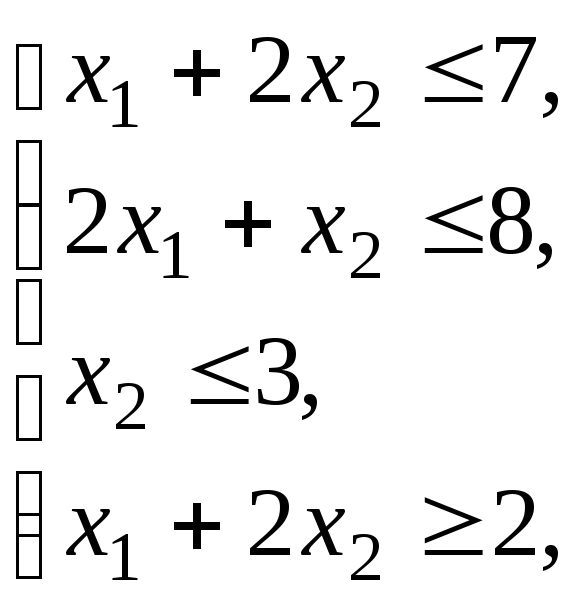
x₁  0, x₂  0.

При решении использовать графический метод.

Решение.

Запишем уравнения граничных прямых и построим их графики на плоскости x₁Оx₂ (рис.1).

l₁ : x₁ + 2x₂ = 7, l₃ : x₂ = 3,

l₂ : 2x₁ + x₂ = 8, l₄ : x₁ + 2x₂ = 2.

Возьмем какую-нибудь пробную точку, например точку О(0; 0) (если это возможно). Выясним, какую полуплоскость определяет каждое неравенство (направления полуплоскостей отмечены стрелками). Определим область допустимых решений (многоугольник АВСDEF) как пересечение полученных полуплоскостей (рис.2).

Строим вектор-градиент(2; 2) и линию уровня c, взяв в качестве c₀ значение ноль: c : 2x₁ + 2x₂ = 0.

Перемещая параллельно самой себе линию уровня С в направлении вектора-градиента (2; 2), находим экстремальную точку Е как точку пересечения прямых l₁ и l₂ (рис.3). Координаты точки Е находим, решив систему из уравнений этих прямых:

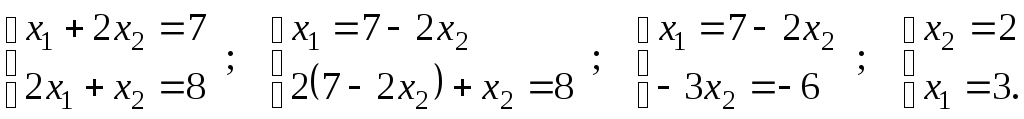
В результате получим точку Е(3; 2).

Вычислим значение целевой функции в полученной точке Е(3; 2):

z(3; 2) = 3 ∙ 2 + 2 ∙ 2 = 10.

Ответ: z_max = 10 при x₁ = 3, x₂ = 2.

Рис. 1 Рис. 2

Рис. 3

1.4. Индивидуальное задание №1

Решить графическим методом задачу оптимизации в условиях следующей модели:

_{1. z = –x1 + x2 + 2  min 2. ­­z = 3x1 + 2x2  max}

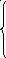
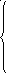_{–x1 + x2  1 x1 + x2  1}

_{3x1 + 2x2  6 –5x1 + x2  0}

_{–3x1 – x2  –9 5x1 – x2  0}

_{x1  0, x2  0 x1 – x2  –1}

_{x1 – x2  4. x1 + x2  6}

_{x1  0, x2  0.}

_{3. z = –x1 + 4x2  max 4. z = –x1 + x2  max}

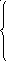
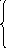_{3x1 + 2x2  12 –2x1 + x2  2}

_{2x1 – x2  0 x1 – 2x2  2}

_{–3x1 + 2x2  3 x1 + x2  5}

_{x1 + 2x2  3 x1  0, x2  0.}

_{x1  0, x2  0.}

_{5. z = 3x1 – x2  min 6. z = –x1 – 2x2  max}

_{2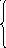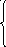x1 + 5x2 – 10  0 x1 – x2  1}

_{2x1 + x2 – 6  0 x1 + x2  2}

_{x1 + 2x2 – 2  0 x1 – 2x2  0}

_{x1  0, x2  0. x1  0, x2  0.}

_{7. z = 2x1 + x2  max 8. z = 3x1 + 4x2  max}

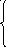
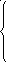_{x1 + x2  20 –1  –x1 + x2  1}

_{0  x1  10 x1 + x2  –1}

_{0  x2  30 –x1 + x2  2}

_{x1 + x2  10. 2x1 – x2  2 x1  0, x2  0.}

9. z = –2x₁ + 5x₂  min 10. z = –x₂ + x₁  min

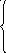
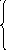7x₁ + 2x₂  14 _{x1 + 3x2  12}

_{5x1 + 6x2  30 3x1 – x2  6}

_{3x1 + 8x2  24 3x1 + 12x2  0}

_{x1  0, x2  0. x1  0, x2  0.}

_{11. z = 2x1 – 3x2  max 12. z = 3x1 – 2x2  min}

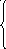
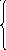4x₁ + 3x₂  12 7x₁ + 2x₂  14

3x₁ + 4x₂  24 –x₁ + 2x₂  2

3x₁ + 8x₂  24 7x₁ + 7x₂  28

x₁  0, x₂  0. x₁  0, x₂  0.

13. z = 6x₁ + x₂  min 14. z = x₁ + x₂  max

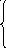
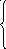x₁ + x₂  3 2x₁ + 5x₂  10

x₁ – x₂  3 –2x₁ + 3x₂  12

–6x₁ + 4x₂  12 2x₁ + 4x₂  20

x₁  2, x₂  8. x₁  0, x₂  0.

15. z = 3x₁ + x₂  max 16. z = 2x₁ + 4x₂  max

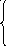
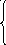–2  x₁ + x₂  2 –x₁ + x₂  1

–2  –x₁ + x₂  2 x₁ + x₂  2

0  x₁  1 0  x₁  10

0  x₂  3  2 . 0  x₂  10.

17. z = 4x₁ + x₂  min 18. z = 2x₁ + x₂ + 4  min

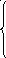
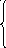x₁ + x₂  2 x₁ + x₂  4

x₁ – x₂  2 8x₁ – 4x₂  16

4x₁ – 4x₂  –8 x₁  2

x₁  1 0  x₂  9.

0  x₂  4.

19. z = –x₁ + 4x₂  max 20. z = 2x₁ + 3x₂  min

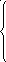
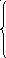3x₁ + 2x₂  12 x₁ + x₂  4

2x₁ – x₂  0 6x₁ + 2x₂  8

–3x₁ + 2x₂  3 x₁ + 5x₂  4

x₁ + 2x₂  3 0  x₂  3

x₁  0, x₂  0. 0  x₁  3.

21. z = 2x₁ + x₂  max 22. z = 2x₁ + x₂  max

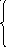
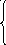–x₁ + x₂  4 x₁ – 2x₂  6

0  x₁  4 x₁ + 3x₂  8

0  x₂  5 0  x₁  4

–x₂ + x₁  0. 0  x₂  2.

23. z = –2x₁ + 5x₂  min 24. z = 5x₁ + x₂  max

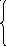7x₁ + 2x₂  8 x₁ + x₂  2

5x₁ + 6x₂  30 x₁ – x₂  2

3x₁ + 8x₂  24 4x₁ + 8x₂  16

x₁  0, x₂  0. x₁  1, 0  x₂  3.

25. z = x₁ + 2x₂  min 26. z = x₁ + 2x₂  min

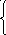2x₁ + 4x₂  8 2x₁ + 4x₂  8

0  x₁  2 –x₁ + 2x₂  2

0  x₂  1. x₁  0, x₂  0.

27. z = 8x₁ + 6x₂  max 28. z = 2x₁ + x₂  max

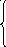
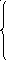4x₁ + 3x₂  12 –x₁ – 2x₂  –4

7x₁ + 5x₂  35 5x₁ + x₂  40

0  x₁  3 2x₁ – 2x₂  7

0  x₂  19  3. x₁ + x₂  4

x₁  0, x₂  0.

29. z = 2x₁ – 3x₂  min 30. z = 3x₁ + x₂  max

–4x₁ + 5x₂  20 10x₁ + 7x₂  70

2x₁ + x₂  6 8x₁ + 10x₂  80

5x₁ – 2x₂  20 x₁  0, x₂  0.

x₁ – x₂  6

x₁  0, x₂  0.

2. СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ

ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

1. Постановка задачи линейного программирования, решаемой

симплексным методом

Решение ЗЛП графическим методом является наглядным и удобным в случае двух переменных. Для случая большего числа переменных графический метод становится невозможным. В этом случае применяют аналитические методы, одним из которых является симплекс-метод.

В зависимости от вида ограничений различают две формы общей модели ЗЛП: каноническую и стандартную.

ЗЛП называется канонической, если ограничения представлены в виде равенств:

z = c₁x₁ + c₂x₂ + … + c_nx_n

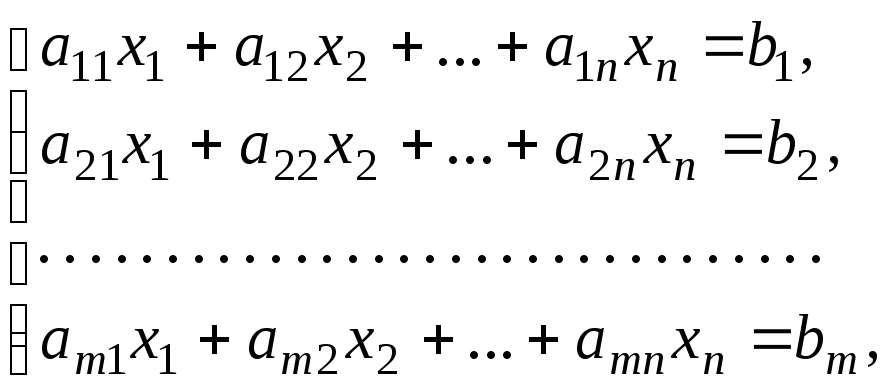
x_j  0, j = 1, 2,…, n, m < n.

Эти соотношения можно записать в векторной форме:

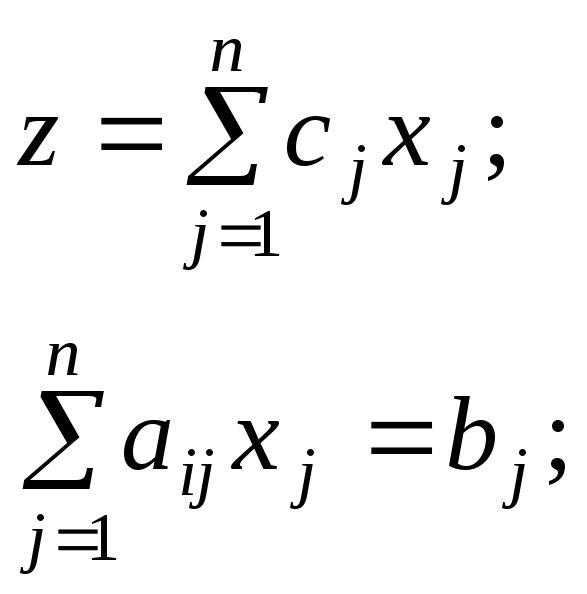
x_j  0; i = 1, 2,…, m; j = 1, 2,…, n; m < n.

ЗЛП называется стандартной, если ограничения представлены в виде неравенств, содержащих знаки ≤ или ≥. В векторной форме эти соотношения имеют вид:

;

или ;

x_j  0, i = 1, 2,…, m, j = 1, 2,…, n, m < n.

Необходимо найти такие значения x₁, x₂, … , x_n, которые обращают в максимум целевую функцию.

Любая стандартная ЗЛП может быть приведена к ЗЛП в каноническом виде с помощью введения неотрицательных переменных x_n+i, которые называют дополнительными. В целевую функцию они входят с нулевыми коэффициентами. В ограничения, содержащие знаки ≤ , дополнительные переменные входят с коэффициентом «1», а в ограничения, содержащие знаки ≥, дополнительные переменные входят с коэффициентом «–1»:

i = 1, 2, …, m ;

или

i = 1, 2, …, m.

При сведении стандартной ЗЛП, имеющей ограничения со знаком ≤, к ЗЛП в каноническом виде, коэффициенты при переменных x_n+i образуют систему m линейно независимых векторов, представляющую базис.

Переменные x_n+1, x_n+2, …, x_n+m называются базисными переменными, а остальные – свободными.

Замечание: Если в системе ограничений из коэффициентов при m переменных x_n+1, x_n+2, …, x_n+m невозможно составить единичную матрицу m-го порядка, то необходимо выбрать базис и найти разложение всех векторов по этому базису.

Из математической модели ЗЛП следует, что в допустимом решении X₀ базисные переменные равны правым частям соответствующих ограничений, а свободные переменные равны нулю: X₀ = (0, 0, …, 0, b₁, b₂, …, b_m).

Симплекс-метод заключается в последовательном улучшении опорного плана путем введения в базис новой переменной и вывода старой, т. е. в таком переходе от старого базиса к новому, чтобы значение целевой функции увеличивалось, если задача решается на отыскании максимума, и уменьшалось, если задача решается на нахождение минимума.

Симплекс-методом ЗЛП решается за конечное число шагов (итераций). На первом шаге отыскивается исходный опорный план, содержащий не более m ненулевых компонент, где m – число строк. На каждом последующем шаге осуществляется нахождение нового опорного плана со значением целевой функции не хуже, чем на предыдущем шаге.

Условия задачи, а также все вычисления при решении ЗЛП симплекс-методом будем оформлять в виде симплекс-таблиц (таблица 1).

При этом в клетках оценочной строки, соответствующих свободным переменным, записываются коэффициенты при свободных переменных в целевой функции, взятые с противоположным знаком (вследствие переноса в левую часть всех переменных в целевой функции).

В клетке оценочной строки, соответствующей свободным членам, записывается значение целевой функции z₀ при первоначальном опорном плане.

Таблица 1

Базисные переменные	Свободные члены	Свободные переменные				Симплексные отношения
		x1	x2	…	xn
xn+1	b1	a11	a12	…	a1n
xn+2	b2	a21	a22	…	a2n
…	…	…	…	…	…
xn+m	bm	am1	am2	…	amn
Оценочная строка	z0	–с1	–с2	…	–сn

Критерием оптимальности опорного плана является отсутствие отрицательных величин в оценочной строке, если решается задача на нахождение максимума целевой функции, и отсутствие положительных величин, если решается задача на отыскание минимума целевой функции.