53 . Критерий Гурвица для импульсных систем .

- упреждение на 1 такт квант.

-запаздывание на 1 такт квант .

P	0	-1
Z	1

 

Для устойчивости системы необходимо и достаточно , чтобы полюса характеристического полинома А*(Z) лежали внутри окружности единичного радиуса . Система нейтральна , если хотя бы один полюс попадает на окружность единичного радиуса . Система неустойчива , если хотя бы один полюс попадает вне окружности единичного радиуса .

 

 

Применение критерия Гурвица к анализу устойчивости импульсных систем .

;

; ;

; ; ;

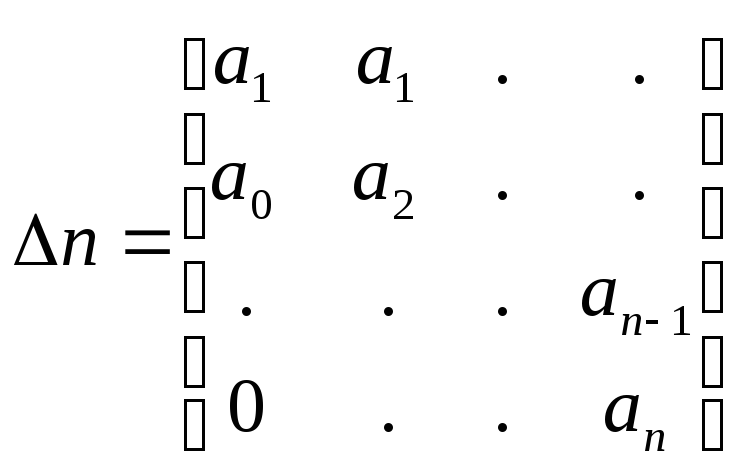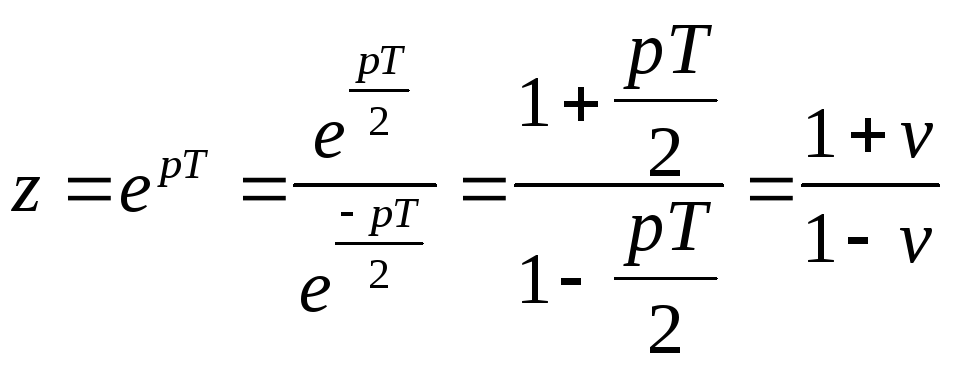Z	1	-1	j	-j	0
V	0	¥	j	-j

 

 

 

54 . Критерий устойчивости Найквиста для импульсных систем .

Критерий устойчивости Найквиста так же как и для непрерывных систем позволяет судить об устойчивости замкнутой импульсной системы по амплитудно-частотной характеристике (АЧХ), или годографу Найквиста, разомкнутой импульсной системы. При этом АЧХ может быть построена экспериментально.

По аналогии с критерием для непрерывных систем сформируем функцию.

С учетом равенства ,

где - полиномы от степени m и n соответственно (mn) ,

 

можно записать

.

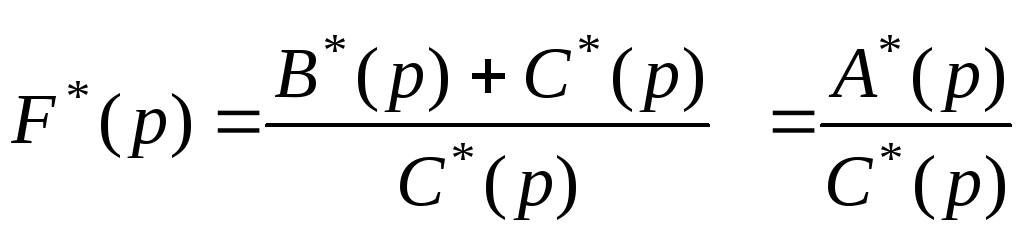Таким образом, функция связывает характеристический полином замкнутой импульсной системы с характеристическим полиномом разомкнутой системы .

Так же как и для случая непрерывных систем, найдем приращение аргумента вектора при изменении частоты в диапазоне : .

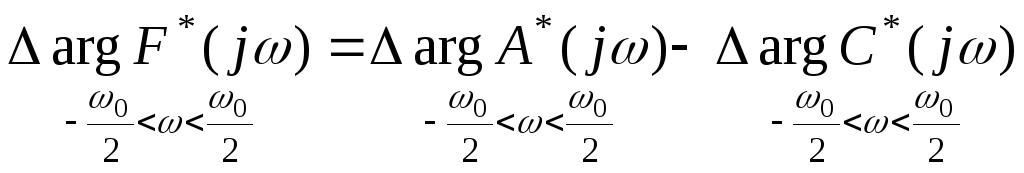или в диапазоне : .

Поскольку мы интересуемся условиями устойчивости замкнутой системы, при выполнении которых все n корней характеристического полинома лежат внутри окружности единичного радиуса, то в соответствии с принципом аргумента для импульсных систем

.

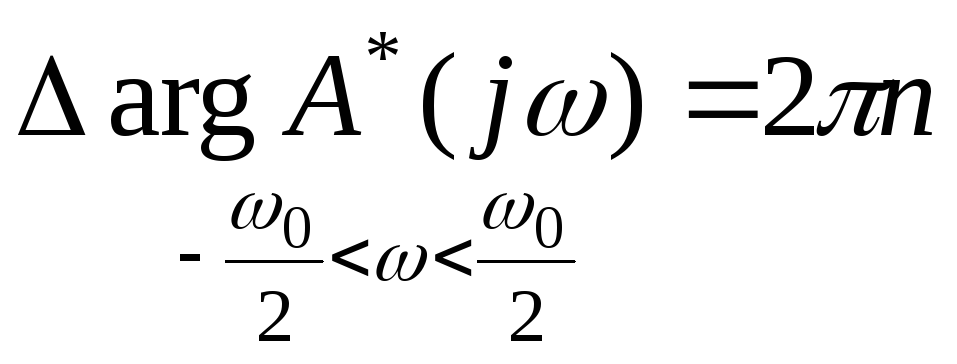
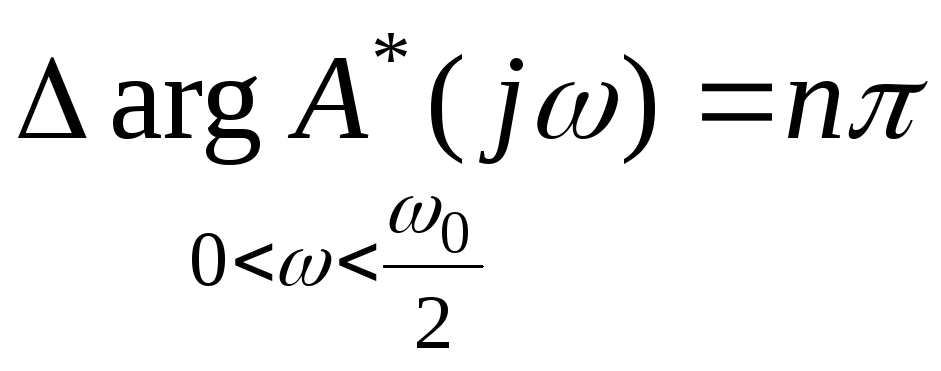Для определения приращения аргумента вектора рассмотрим три случая:

1. a)      Разомкнутая импульсная система устойчива, т.е. все n корней ее характеристического полинома лежат внутри окружности единичного радиуса. Тогда в соответствии с принципом аргумента

и

а приращение аргумента функции будет равно нулю в соответствии с выражениями

и

.

Рассмотрим геометрическую интерпретацию этой ситуации.

На рис.1.11 а представлен график функции , для которой изменение аргумента при изменении частоты в диапазоне равно нулю, а на рис. 1.11 б - график соответствующей ей .

 

 

а б

Рис.1.11

Сформируем критерий устойчивости Найквиста для этого случая

Если разомкнутая импульсная система устойчива, то для устойчивости замкнутой импульсной системы необходимо и достаточно, чтобы амплитудно-частотная характеристика разомкнутой системы не охватывала точку с координатами (-1, j0).

2. b)      Разомкнутая импульсная система неустойчиваи L корней ее характеристического уравнения лежат вне окружности единичного радиуса (соответственно n-L корней лежат внутри единичной окружности). В соответствии с принципом аргумента

и .

Приращение аргумента функцииможет быть найдено из выражений :

и

Геометрическая интерпретация этой ситуации представлена

на рис.1.12. При этом на рис.1.12 а представлен годограф функции , для которой изменение аргумента при изменении частоты в диапазоне равно 2(L – число корней ,лежащих вне единичной окружности), а на рис. 1.12 б - годограф соответствующей ей функции .

 

 

 

 

 

 

 

 

 

 

Рис.1.12

Заметим, что годограф охватывает точку с координатами (0,0) один раз в положительном направлении (против часовой стрелки), аналогично годограф охватывает точку с координатами (-1,j0) в положительном направлении один раз .