- •26. Критерий устойчивости Гурвица. Пример.
- •27. Принцип аргумента. Критерий устойчивости Михайлова.
- •29. Критерий устойчивости Найквиста для неустойчивой в разомкнутом состянии системы.
- •30. Критерий устойчивости Найквиста для нейтральной в разомкнутом состянии системы.
- •31. Общая формулировка критерия Найквиста. Логарифмический критерий устойчивости.
- •32. Прямые показатели качества сау. Косвенные показатели:
- •36. Синтез систем по логарифическим частотным характеристикам разомкнутой системы. Построение желаемой лачх.
- •37. Последовательная и параллельная коррекция. Алгоритм выбора корректирующего устройства. Пример.
- •40. Построение корректирующего устройства при последовательной и параллельной коррекции на примере следящей системы.
- •Последовательная коррекция
- •41. Дискретные системы автоматического управления. Типы дискретизации. Структурные схемы импульсных систем.
- •42. Понятие решетчатой и модулированной функций. Дискретное преобразование Лапласа.
- •43. Свойства дискретного преобразования Лапласа.
- •44. Дискретные передаточные функции. Дискретные типовые сигналы и их изображение.
- •45. Весовая и импульсная переходная характеристики дискретной системы на примере временных характеристик дискретных интегрирующегго и инерционного звеньев.
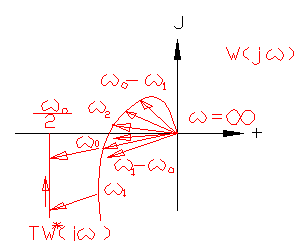
- •46. Частотные характеристики импульсных систем.
- •53 . Критерий Гурвица для импульсных систем .
- •54 . Критерий устойчивости Найквиста для импульсных систем .
- •Сформируем критерий устойчивости Найквиста для этого случая
- •Сформулируем критерий устойчивости Найквиста для случая б).
- •Общая формулировка критерия Найквиста
- •55 . Качество импульсных систем . Пример расчета ошибок импульсной системы . Импульсные системы с конечным временем переходного процесса .
- •Прямые показатели качества
- •Косвенные показатели качества
- •Частотные методы анализа качества импульсных систем По годографу разомкнутой импульсной системы
- •Точность замкнутых импульсных систем
- •56 . Нелинейные сау . Типовые н . Э .
- •57 . Структурные схемы нелинейных сау . Некоторые правила их преобразования .
- •58 . Основные понятия фазовой плоскости , свойства фазовых траекторий . Примеры .
- •59 . Метод изоклин . Исследование н . Систем 2-го порядка на фазовой плоскости , типы особых точек .
- •60 . Исследование релейной сау методом фазовой плоскости .
- •61 . Коррекция релейных систем по скорости .
- •62 . Коррекция релейных систем с помощью жесткой обратной связи .
- •63 . Особенности динамики нелинейных систем . Скользящий режим .
- •Экзаменационные вопросы по оау.
- •Лектор Ягодкина т.В.
- •1.Из истории автоматики.
- •2. Основные понятия автоматики. Функциональная схема сау.
- •Управление в технических системах. Цели упровления в технических системах.
- •Упрощенная функциональная схема сау.
- •3. Классификация сау.
- •4. Принципы автоматического регулирования, законы регулирования.
- •1. Пропорциональный закон регулирования (“п”).
- •2. Интегральный закон регулирования («и»).
- •4. Пропорционально-интегральный закон регулирования («пи»).
- •4. Пропорционально-интегрально-дифференциальный закон регулирования («пид»).
- •5. Статическая система автоматического управления на примере сар скорости вращения двигателя постоянного тока с независимым возбуждением.Статические характеристики сар.
- •1. «И» закон регулирования.
- •2. Пропорциональный закон регулирования.
- •6. Линеаризация. Вывод уравнений генератора постоянного тока с рабочей точкой в нелинейной зоне.
- •Получение линеаризованныхуравнений
- •Получение линеаризованных уравнений гпт для рабочей точки в нелинейной зоне
- •7. Линеаризация. Вывод уравнений генератора постоянного тока с рабочей точкой в линейной зоне.
- •8. Свойства преобразования Лапласа. Передаточные функции.
- •9. Частотные характеристики сау: комплексный коэффициент усиления, ачх, фчх, вчх,мчх,афх,лачх,лфчх. Частотные характеристики сау.
- •10. Частотные характеристики интегрирующего и инерционного звеньев.
- •11. Частотные характеристики колебательного и звена запазды- вания.
- •Звено запаздывания
- •15. Временные характеристики сау и способы их построения по: дифференциальным уравнениям, вещественным частотным характеристикам, структурным схемам.
- •16. Временные характеристики сау и способы их построения по
42. Понятие решетчатой и модулированной функций. Дискретное преобразование Лапласа.
Математическим аппаратом для исследования импульсных систем является дискретное преобразование Лапласа.
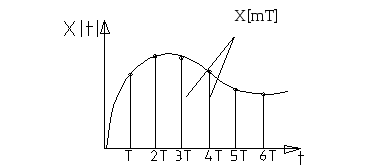
х[mT]-решетчатая функция, состоит из ординат;
Модулированный
сигнал (последовательность
![]() -функций,
модулированная ординатами входного
сигнала в дискретные моменты времени).
-функций,
модулированная ординатами входного
сигнала в дискретные моменты времени).

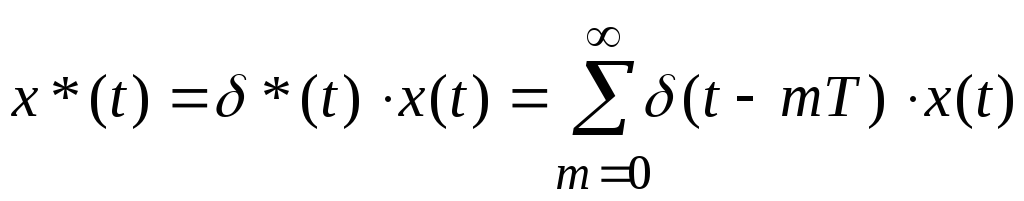 ;
;
![]()
 ;
;
Сигнал
![]() -реально
существующий сигнал;
-реально
существующий сигнал;
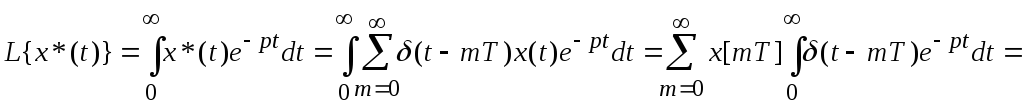
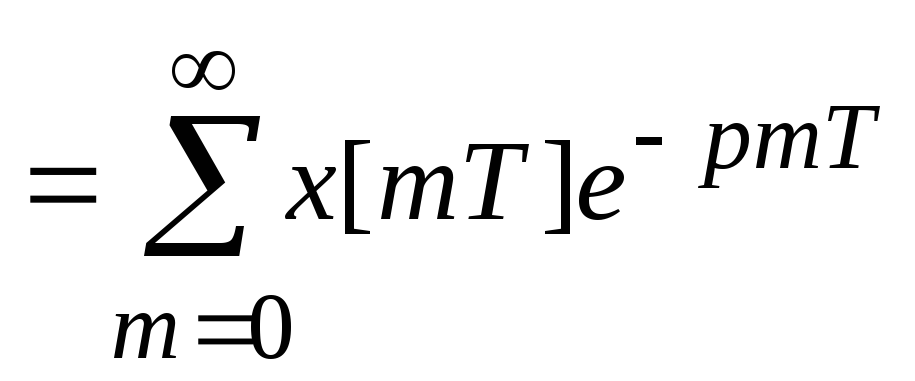 ;
;
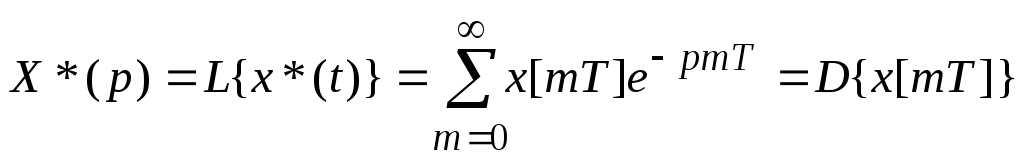 ;
;
D-дискретное преобразование Лапласа.
43. Свойства дискретного преобразования Лапласа.
1. Линейность.
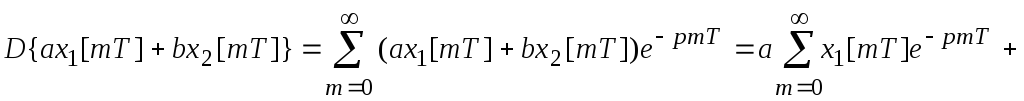
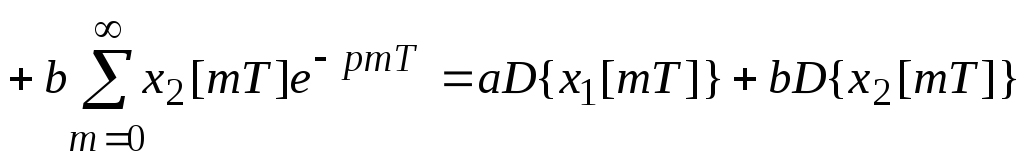 ;
;
2. (Преобразование Лапласа от запаздывающего аргумента). Смещение по времени.
а) Запаздывание на Sтактов.
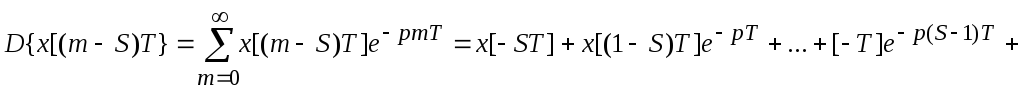

![]() ;
где i=m-S.
;
где i=m-S.
При нулевых начальных условиях (ННУ):
![]() ;
;
![]() ;
;
б) Упреждение m+S=i; m=i-S;

![]() ;
при не ННУ
;
при не ННУ
При ННУ:
![]() ;
;
![]() ;
;
3. Преобразование Лапласа от конечных разностей.
Первая разность
-
![]() ;
;
 ;
;
При ННУ:
![]() ;
;
Непрерывные системы-p;
Дискретные
системы-![]() ;
;
Вторая разность-![]()
![]() ;
;
При ННУ:
![]()
![]() ;
;
![]() -к-ая
разность-
-к-ая
разность-
![]() ;
;
4. Преобразование от суммы:
Найдем первую разность.
 ;
;
Возьмем преобразования Лапласа от правой и левой части выражения.
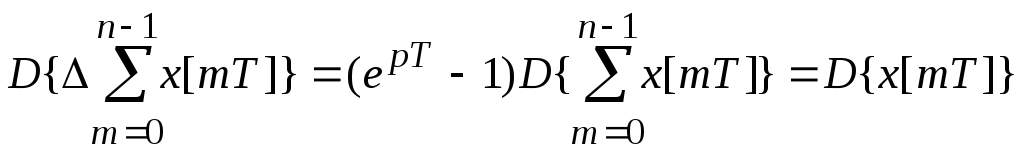 ;
;
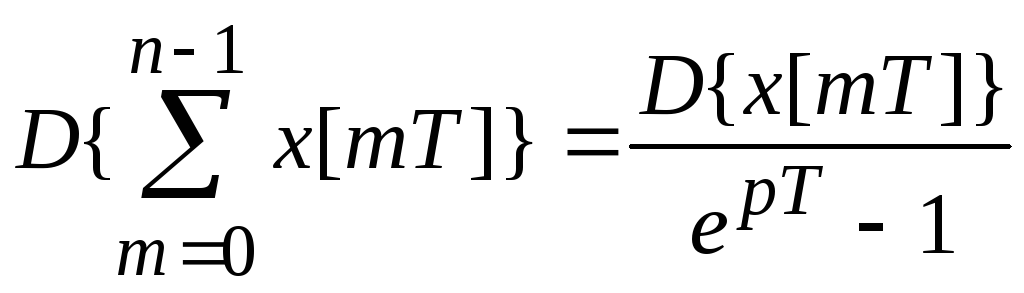 ;
;
5. Теорема о предельном значении.
По анологии с
непрерывными системами:![]() ;
;
6. Сумма ординат решетчатой функции.
 ;
;
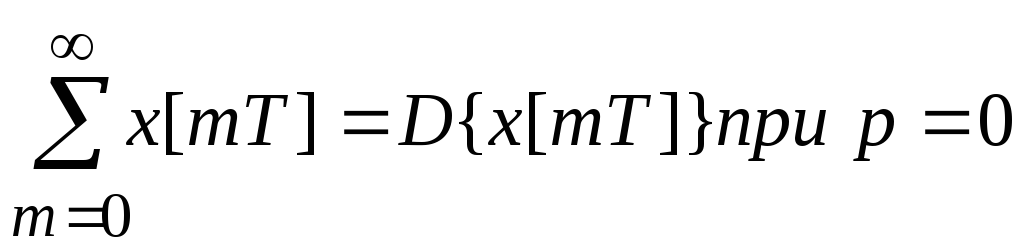 ;
;
44. Дискретные передаточные функции. Дискретные типовые сигналы и их изображение.
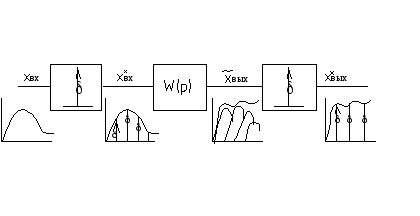
Для
непрерывных систем:
![]() при ННУ;
при ННУ;
 Для
дискретной системы:
Для
дискретной системы:
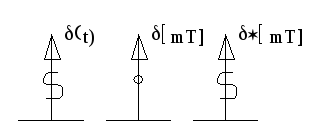
![]() при ННУ;
при ННУ;
1. Дельта-функция.
![]() ;
;
 ;
;
2. Единичная ступенчатая функция.(1(t))
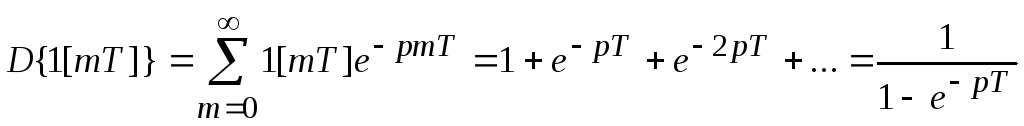 ;
;
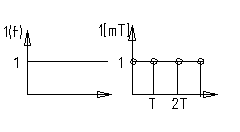 Это
бесконечно убывающая прогрессия:
Это
бесконечно убывающая прогрессия:
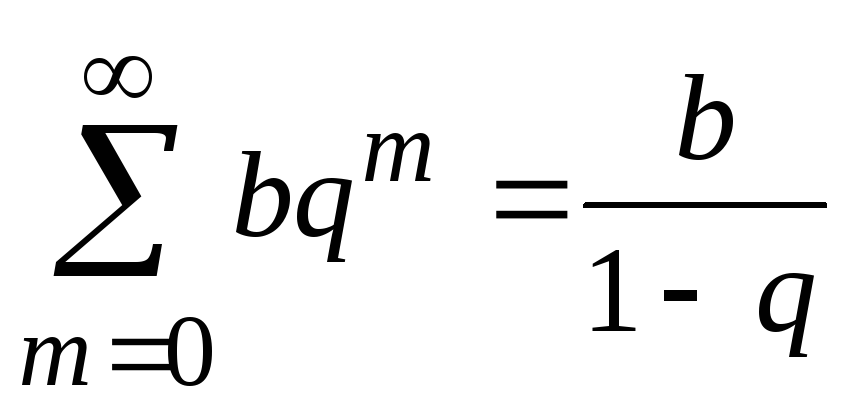 ;
;
3. Линейно возрастающая функция.
![]()


![]()
![]()
 ;
;
4. Экспонента.
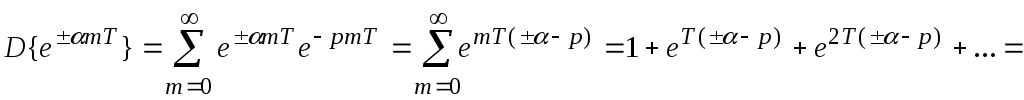
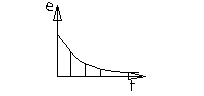
![]() ;
;
![]() ;
;
45. Весовая и импульсная переходная характеристики дискретной системы на примере временных характеристик дискретных интегрирующегго и инерционного звеньев.
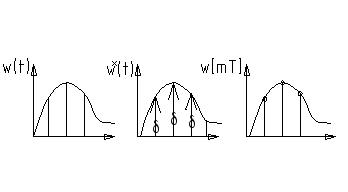
![]() -дискретное
преобразование Лапласа от весовой
функции непрерывного преобразования;
-дискретное
преобразование Лапласа от весовой
функции непрерывного преобразования;
![]() ;
;
Назовем
всё это преобразование
![]() .
.
Весовая функция не меняется (или инвариантна) при дискретизации входного и выходного сигнала.
![]() ,
условие корни А(p) простые
(не кратные),m<n,
гдеm-степень числителя,
аn-степень знаменателя.
,
условие корни А(p) простые
(не кратные),m<n,
гдеm-степень числителя,
аn-степень знаменателя.
![]() получаем
по формуле разложения:
получаем
по формуле разложения: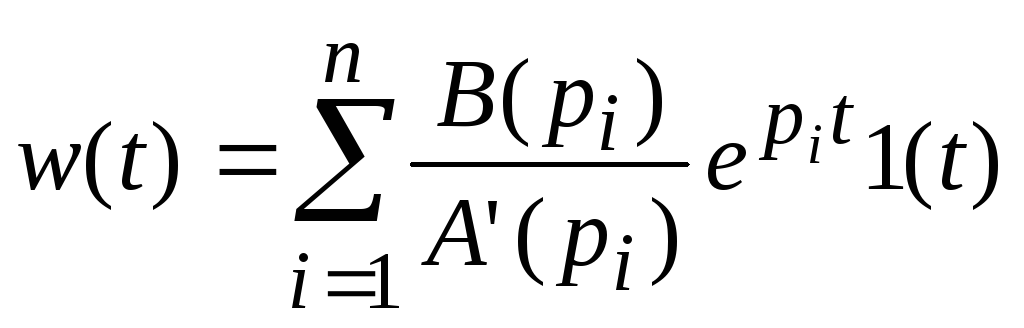 ;
;
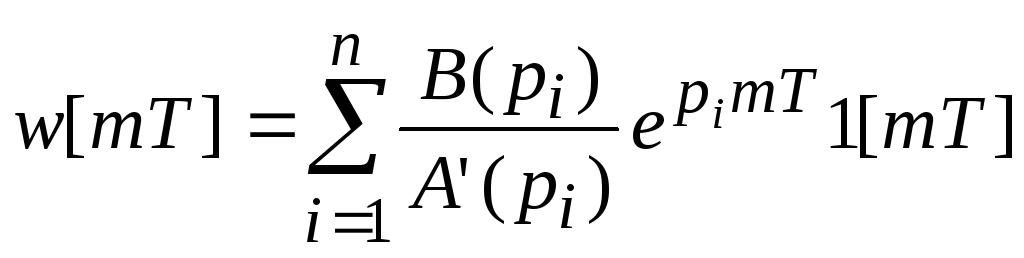 ;
;
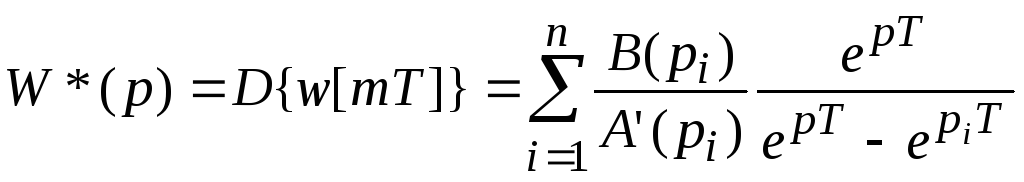 ;
;
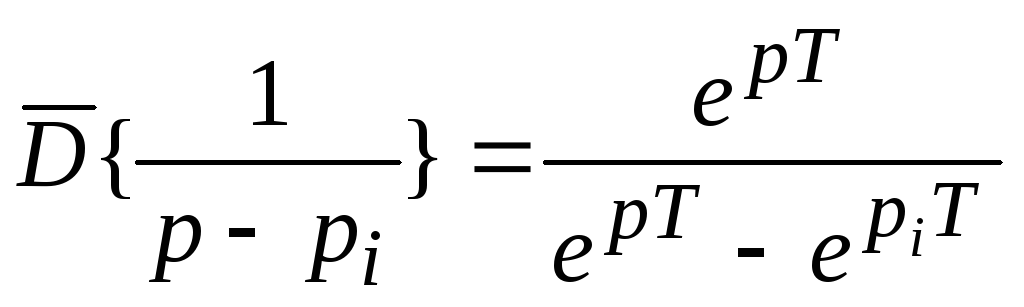
 ;
;
Переходная функция.
![]() ;
;
Переходная функция импульсной системы не равна переходной функции непрерывной системы, хотя и близка к ней.
П римеры:
римеры:
Построение весовой функции интегрирующего звена (дискретного).
![]() ;
;
![]() ;
;
Построение весовой функции инерционного звена.
Остаток
от деления
|
|
![]()
 ;
К1=К/Т1;
;
К1=К/Т1;
Поделим
числитель на знаменатель:
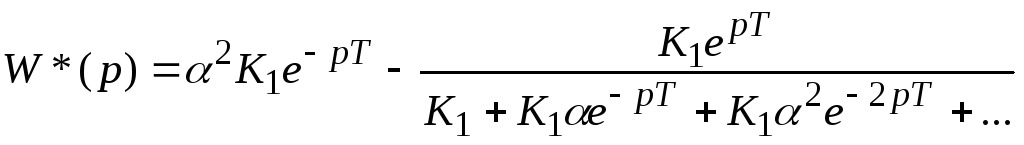 ;
;
Частное
|
|

![]() при
t=mT;
при
t=mT;
Построение переходной функции дискретного интегрирующего звена по разностному уравнению.
![]()
![]() ;
;
![]() ;
;
Операторное
уравнение:![]() ;
;
![]() ;
;
![]() ;
;
![]() ННУ;
ННУ;
Рекурентная
формула:
![]() ;
;
![]() ;
;
![]() ;
;
![]() и т.д.
и т.д.
С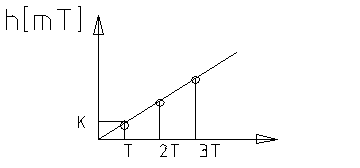 троим
переходную функцию:
троим
переходную функцию:
Построение переходной функции инерционного звена.
![]()
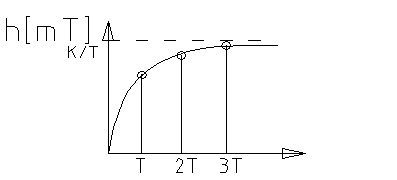 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Рекурентная
формула:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() и т.д.
и т.д.
![]() ;
;
46. Частотные характеристики импульсных систем.
Комплексный
коэффициент усиления непрерывной
системы:
![]() приp=jw;
приp=jw;
Дискретная
система:
![]() приp=jw;
приp=jw;
Далее см. вопрос №47 с примерами построения АФХ.
47. Примеры построения частотных характеристик дискретного интегрирующего и инерционного звеньев .
W(jw)=W(p) çp = jw
ННУ НПФ
W*(jw)=W*(p) çp = jw
W(p)®w(t)®w[mT]®W*(p)
Интегрирующее звено .
W(p)=K/P ; w(t)=L-1{K/P}=K 1(t)
w[mT]=Д{K
1[mT]}= =![]()
![]()
![]()
![]()
![]()
![]()

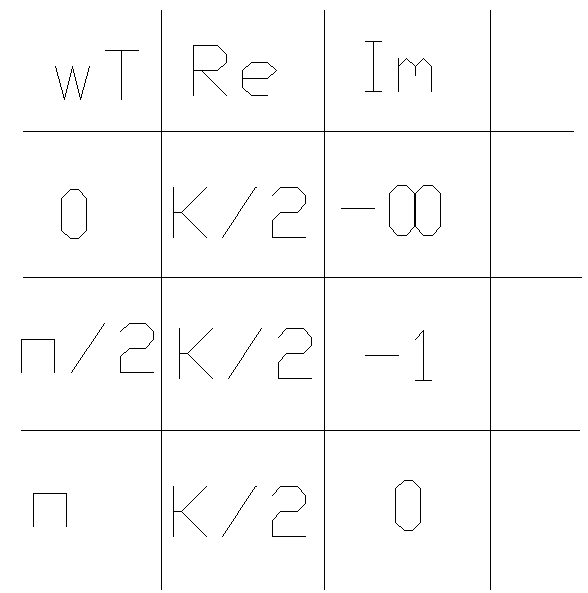

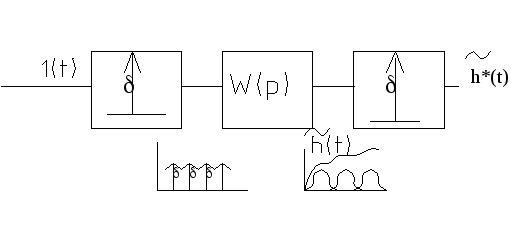
Импульсные системы первого и второго порядков могут быть неустойчивыми .
Инерционное звено .
![]()
![]()
![]()
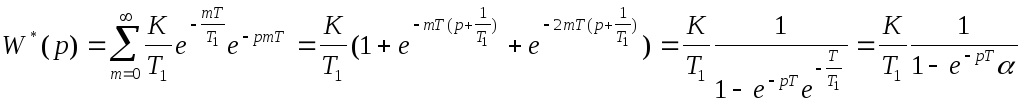
![]()
![]()
![]()
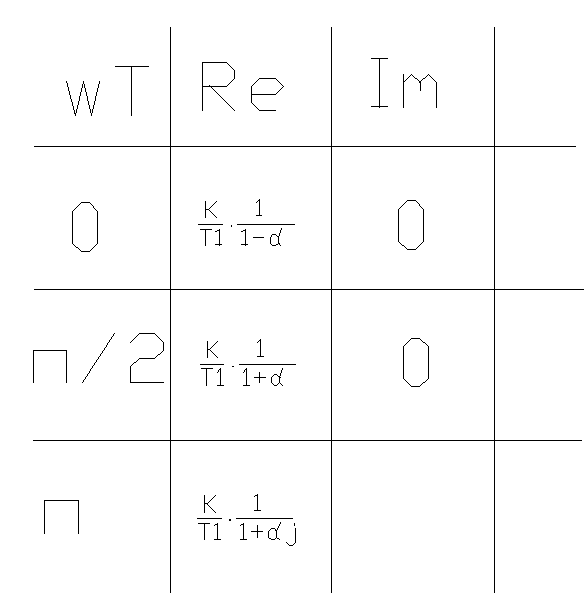

![]()
48 . Связь изображений и частотных характеристик дискретных и непрерывных сигналов . Теорема Котельникова .
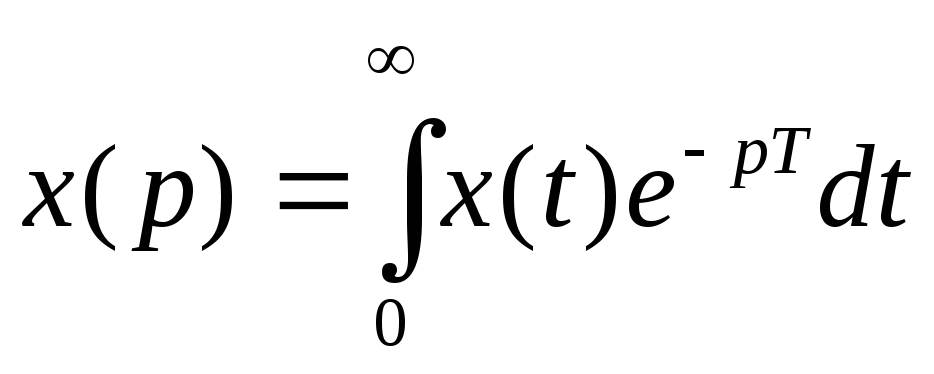
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
49 . Связь между дискретной и непрерывной передаточной функцией . Построение годографа дискретной системы по годографу непрерывной .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
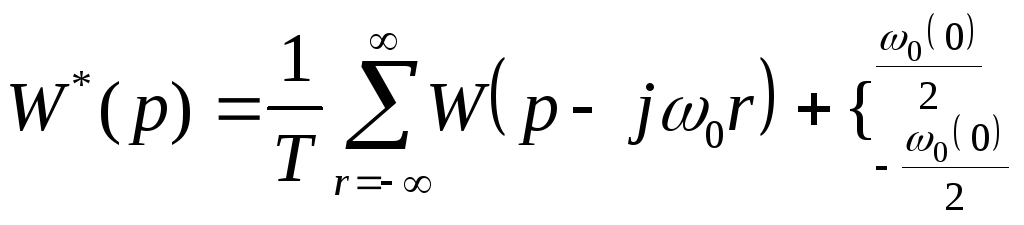
![]()
Построение годографа дискретной системы по годографу непрерывной .
![]()
|
|
| |
|
|
| |
|
|
|
|
50 . Передаточные функции дискретных замкнутых систем .
схема 1

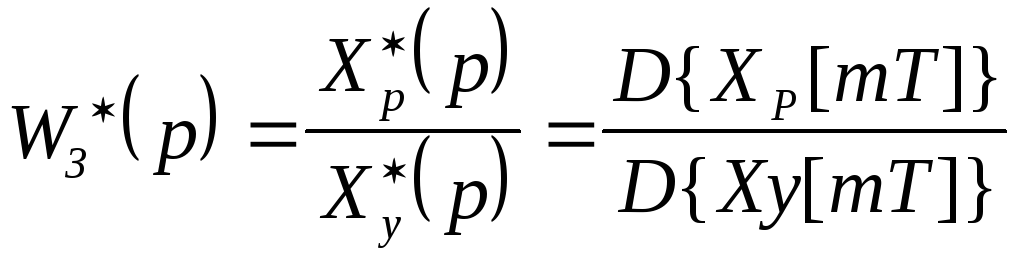

схема 1 Þ
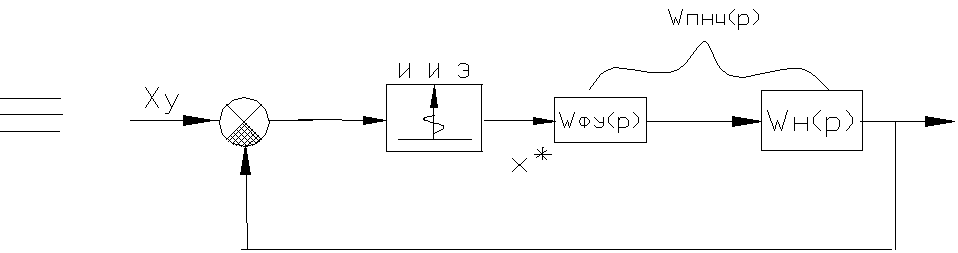

Уравнение
сумматора :
![]() ;
;
Звена
:
![]() ;
;
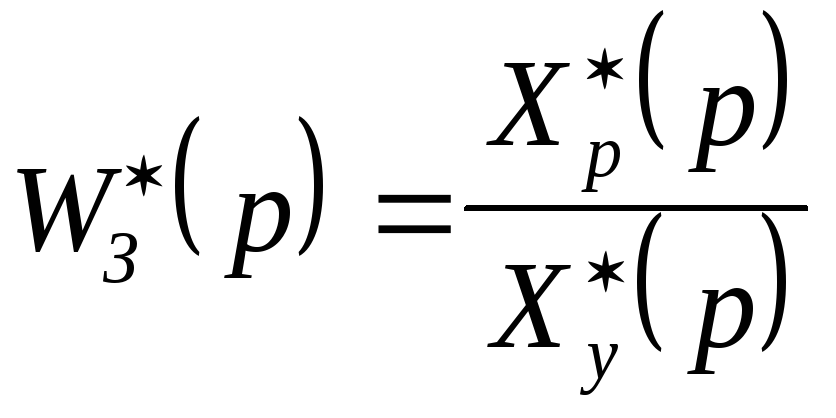 ;
;
Свойство
![]() преобразования
преобразования
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
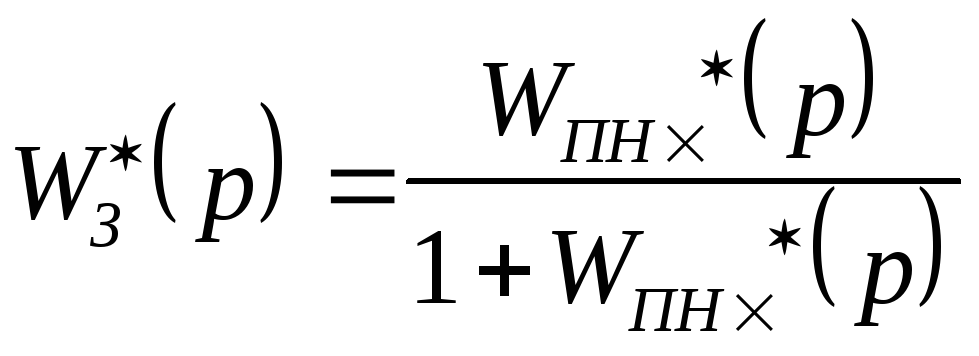 ;
;
 .
.
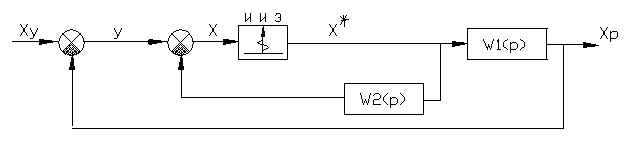
51 . Структурные схемы импульсных систем . Некоторые правила их преобразований .
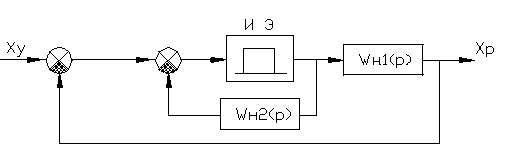
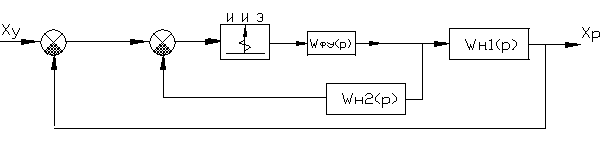
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
 ;
;
![]() преобразование :
преобразование :
![]()
![]()
![]()
![]()
![]()
![]() ;
;
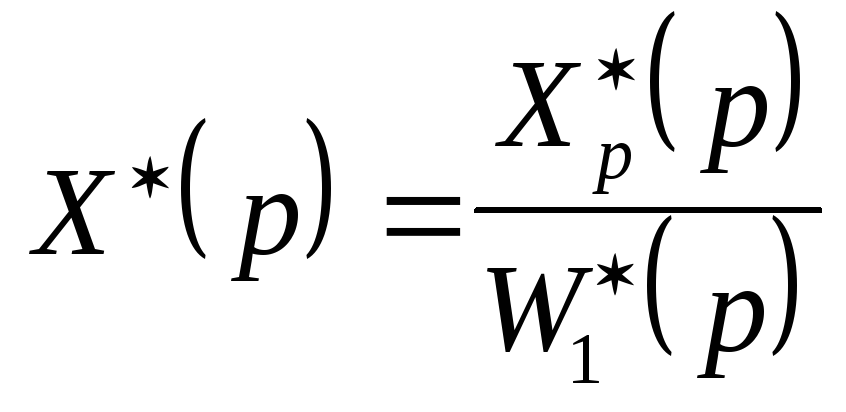 ;
;
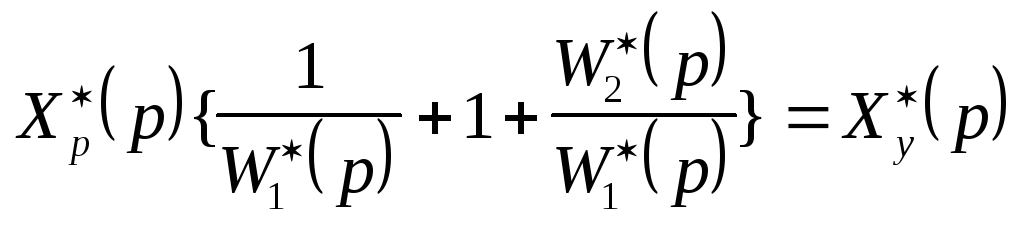 ;
;
 ;
;
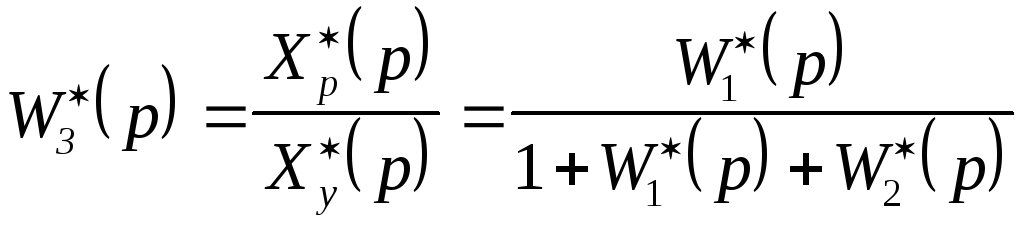 ;
;
2-ой способ :
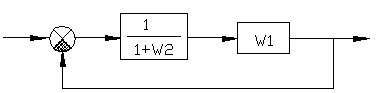
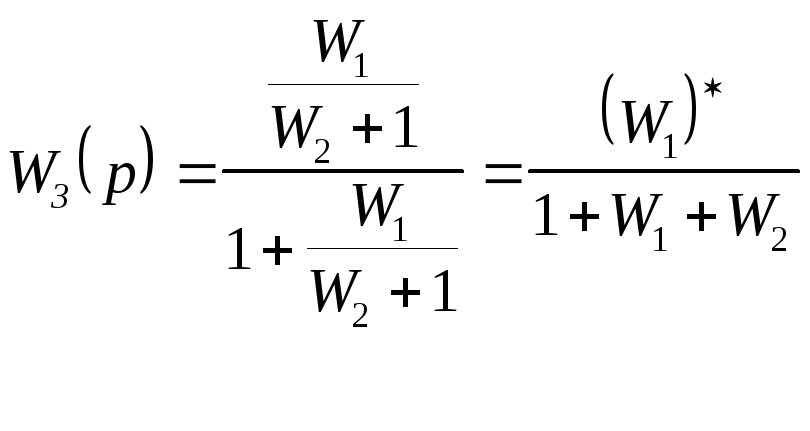 ;
;
Правила структурного преобразования импульсных систем :
В непрерывной части импульсной системе можно производить любые преобразования .
Нельзя переставлять передаточную функцию и импульсный элемент .
Когда
импульсный элемент стоит на входе
системы , можно написать передаточную
функцию непрерывной замкнутой системы
, а затем проставить звездочки .
![]()
52 . Устойчивость импульсных систем . Необходимые и достаточные условия устойчивости .
Система устойчива , если после снятия кратковременного воздействия она возвращается в исходное состояние .
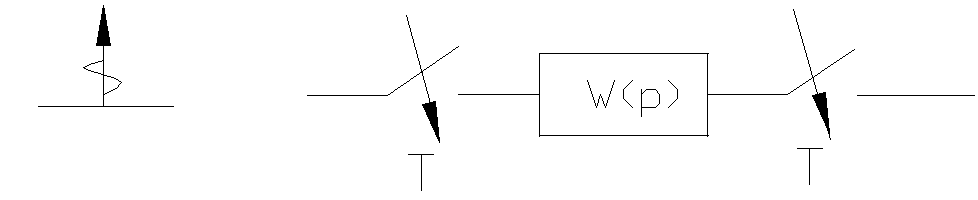
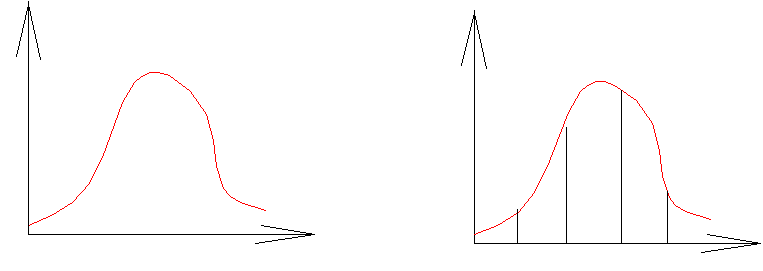
![]() Если непрерывная
система устойчива , то импульсная система
будет также устойчива .
Если непрерывная
система устойчива , то импульсная система
будет также устойчива .
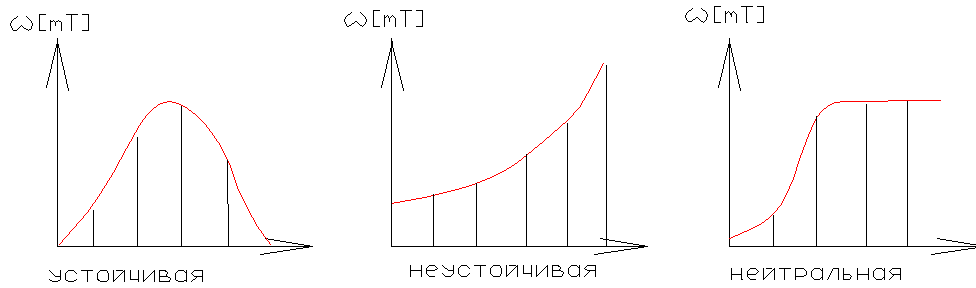
Необходимое и достаточное условие устойчивости импульсных систем .
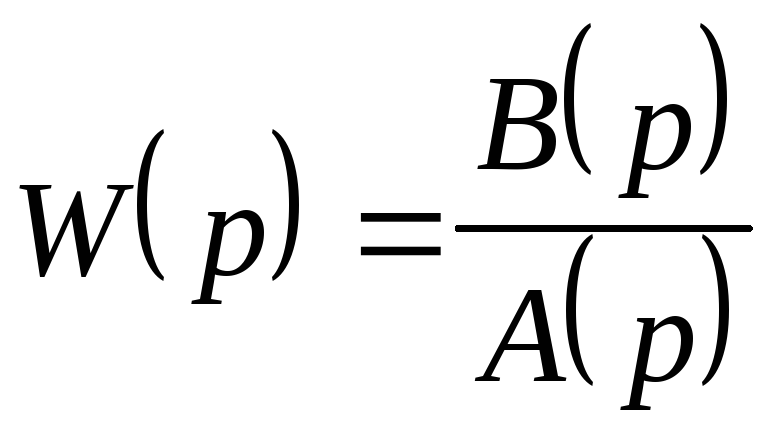 -корни
-корни
![]() ;
;
![]() ;
;
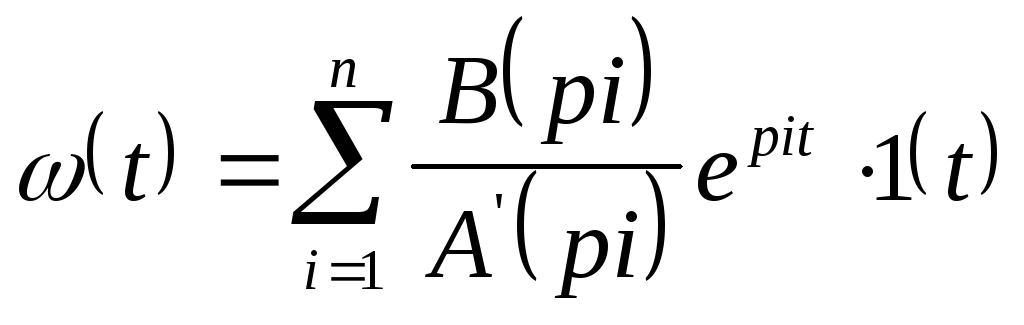 - форма разложения
.
- форма разложения
.
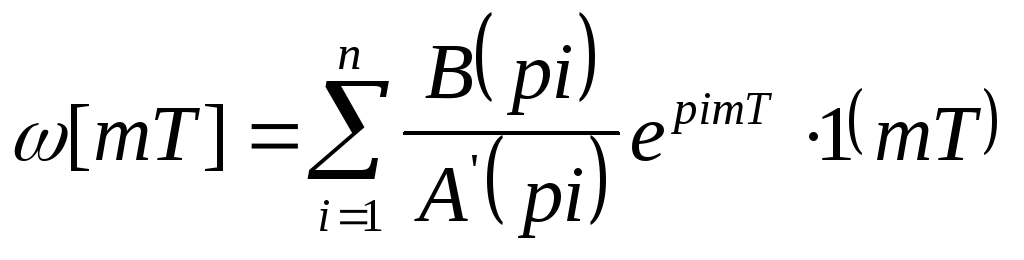 ;
;
 ;
;
![]() ;
;
![]() ;
(
;
(
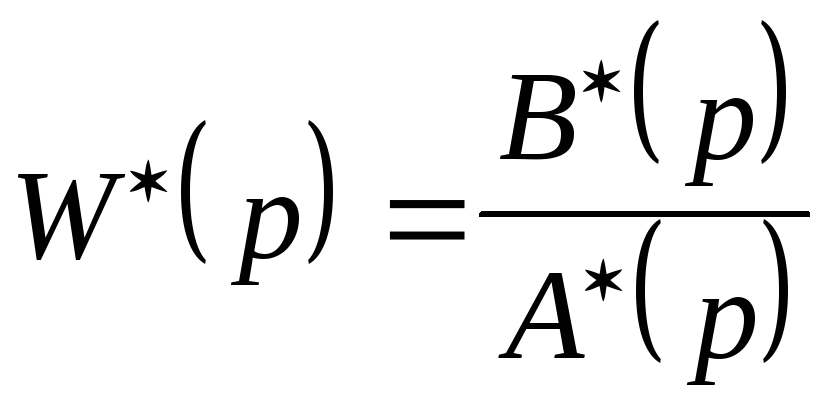 ) ;
) ;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ; ( корни
; ( корни
![]() ,
,
![]() )
.
)
.
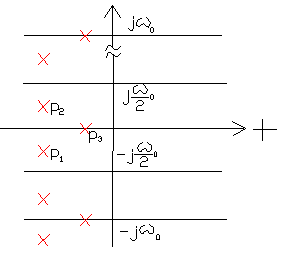
|
|
Для устойчивости импульсной системы необходимо и достаточно , чтобы полюса ее дискретной передаточной функции лежали в левой части комплексной плоскости . Система нейтральна , если хотя бы один из них попадает на ось . | |
|
Система неустойчива , если хотя бы один попадает в правую часть плоскости . |
| |
|
|
|
|