
- •26. Критерий устойчивости Гурвица. Пример.
- •27. Принцип аргумента. Критерий устойчивости Михайлова.
- •29. Критерий устойчивости Найквиста для неустойчивой в разомкнутом состянии системы.
- •30. Критерий устойчивости Найквиста для нейтральной в разомкнутом состянии системы.
- •31. Общая формулировка критерия Найквиста. Логарифмический критерий устойчивости.
- •32. Прямые показатели качества сау. Косвенные показатели:
- •36. Синтез систем по логарифическим частотным характеристикам разомкнутой системы. Построение желаемой лачх.
- •37. Последовательная и параллельная коррекция. Алгоритм выбора корректирующего устройства. Пример.
- •40. Построение корректирующего устройства при последовательной и параллельной коррекции на примере следящей системы.
- •Последовательная коррекция
- •41. Дискретные системы автоматического управления. Типы дискретизации. Структурные схемы импульсных систем.
- •42. Понятие решетчатой и модулированной функций. Дискретное преобразование Лапласа.
- •43. Свойства дискретного преобразования Лапласа.
- •44. Дискретные передаточные функции. Дискретные типовые сигналы и их изображение.
- •45. Весовая и импульсная переходная характеристики дискретной системы на примере временных характеристик дискретных интегрирующегго и инерционного звеньев.
- •46. Частотные характеристики импульсных систем.
- •53 . Критерий Гурвица для импульсных систем .
- •54 . Критерий устойчивости Найквиста для импульсных систем .
- •Сформируем критерий устойчивости Найквиста для этого случая
- •Сформулируем критерий устойчивости Найквиста для случая б).
- •Общая формулировка критерия Найквиста
- •55 . Качество импульсных систем . Пример расчета ошибок импульсной системы . Импульсные системы с конечным временем переходного процесса .
- •Прямые показатели качества
- •Косвенные показатели качества
- •Частотные методы анализа качества импульсных систем По годографу разомкнутой импульсной системы
- •Точность замкнутых импульсных систем
- •56 . Нелинейные сау . Типовые н . Э .
- •57 . Структурные схемы нелинейных сау . Некоторые правила их преобразования .
- •58 . Основные понятия фазовой плоскости , свойства фазовых траекторий . Примеры .
- •59 . Метод изоклин . Исследование н . Систем 2-го порядка на фазовой плоскости , типы особых точек .
- •60 . Исследование релейной сау методом фазовой плоскости .
- •61 . Коррекция релейных систем по скорости .
- •62 . Коррекция релейных систем с помощью жесткой обратной связи .
- •63 . Особенности динамики нелинейных систем . Скользящий режим .
- •Экзаменационные вопросы по оау.
- •Лектор Ягодкина т.В.
- •1.Из истории автоматики.
- •2. Основные понятия автоматики. Функциональная схема сау.
- •Управление в технических системах. Цели упровления в технических системах.
- •Упрощенная функциональная схема сау.
- •3. Классификация сау.
- •4. Принципы автоматического регулирования, законы регулирования.
- •1. Пропорциональный закон регулирования (“п”).
- •2. Интегральный закон регулирования («и»).
- •4. Пропорционально-интегральный закон регулирования («пи»).
- •4. Пропорционально-интегрально-дифференциальный закон регулирования («пид»).
- •5. Статическая система автоматического управления на примере сар скорости вращения двигателя постоянного тока с независимым возбуждением.Статические характеристики сар.
- •1. «И» закон регулирования.
- •2. Пропорциональный закон регулирования.
- •6. Линеаризация. Вывод уравнений генератора постоянного тока с рабочей точкой в нелинейной зоне.
- •Получение линеаризованныхуравнений
- •Получение линеаризованных уравнений гпт для рабочей точки в нелинейной зоне
- •7. Линеаризация. Вывод уравнений генератора постоянного тока с рабочей точкой в линейной зоне.
- •8. Свойства преобразования Лапласа. Передаточные функции.
- •9. Частотные характеристики сау: комплексный коэффициент усиления, ачх, фчх, вчх,мчх,афх,лачх,лфчх. Частотные характеристики сау.
- •10. Частотные характеристики интегрирующего и инерционного звеньев.
- •11. Частотные характеристики колебательного и звена запазды- вания.
- •Звено запаздывания
- •15. Временные характеристики сау и способы их построения по: дифференциальным уравнениям, вещественным частотным характеристикам, структурным схемам.
- •16. Временные характеристики сау и способы их построения по
37. Последовательная и параллельная коррекция. Алгоритм выбора корректирующего устройства. Пример.
Последовательная коррекция.
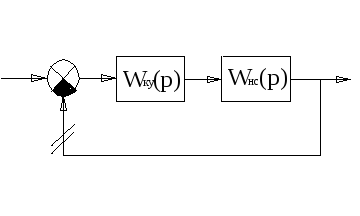
К.У. вносится в прямую цепь. Систему размыкаем.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
 При
последовательной коррекции ЛАЧХ
корректирующего устройства равна
разностной ЛАЧХ.
При
последовательной коррекции ЛАЧХ
корректирующего устройства равна
разностной ЛАЧХ.
Параллельная коррекция.
Синтез осуществляется по разомкнутой системе.
![]() ;
;
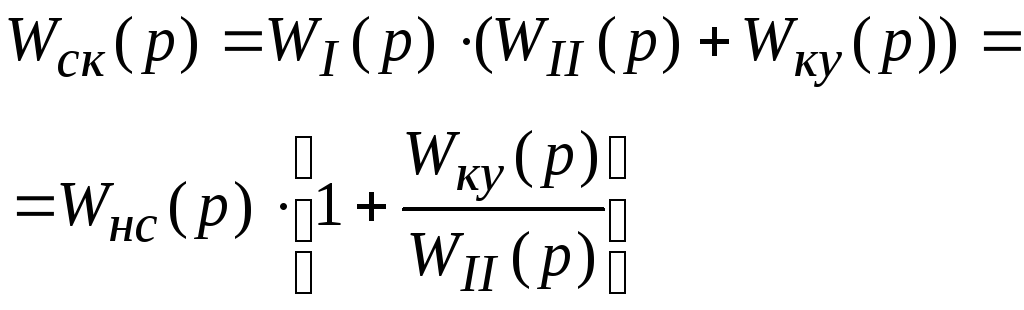
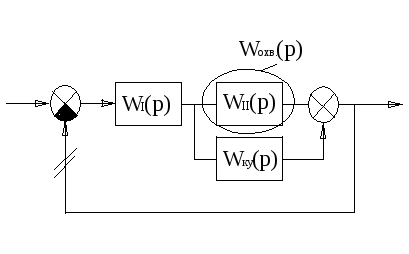
Назовем то, что в скобках W0(p)-разностная передаточная функция.
![]() ;
;
![]() ;
;
![]()
![]() ;
;
Алгоритм:
1. Находится разностная ЛАЧХ
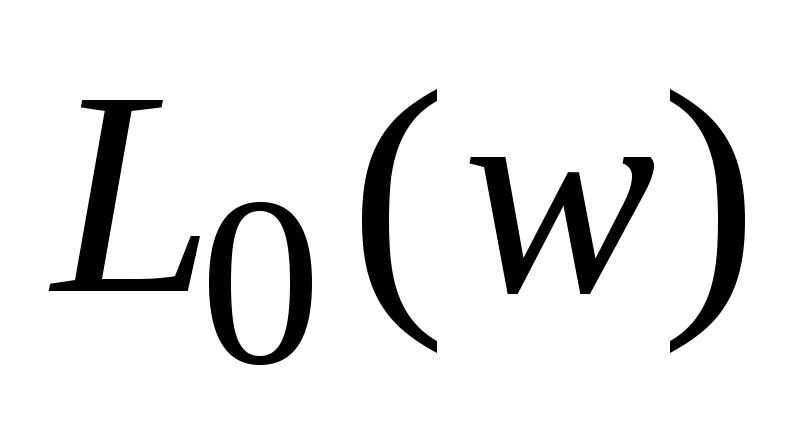 ,
по ней восстанавливается
,
по ней восстанавливается
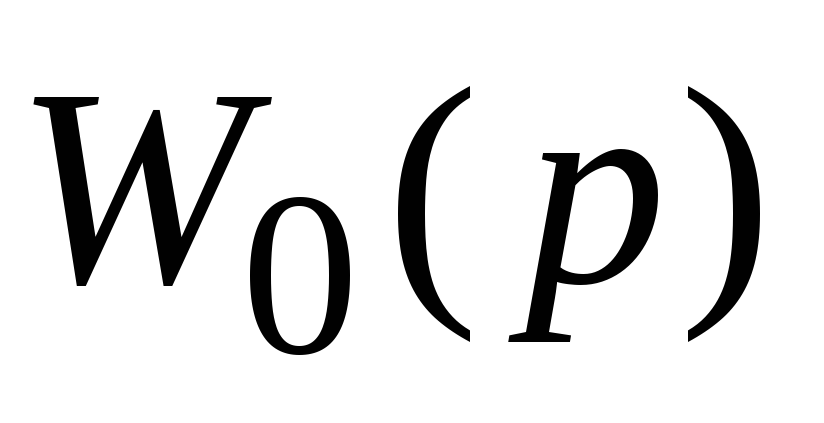 .
.2. По формулам (*) определяется
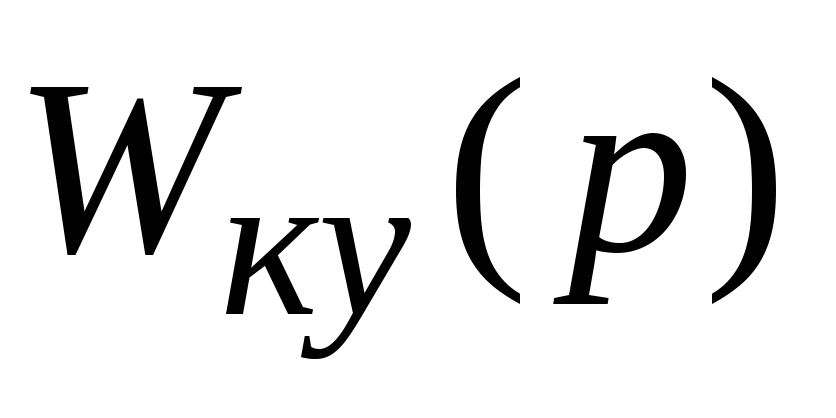 :
:
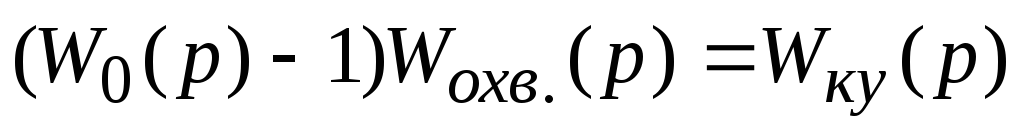 ;
;
 38.
Коррекция в цепи обратной связи. Алгоритм
выбора корректирующего устройства.
Пример.
38.
Коррекция в цепи обратной связи. Алгоритм
выбора корректирующего устройства.
Пример.
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]() ;
;
Алгоритм:
1. Находим разностную ЛАЧХ
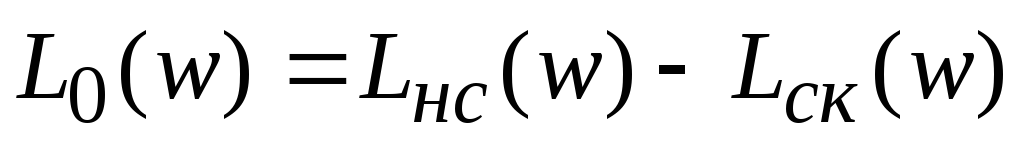 ;
;
а) Рассматриваем
область частот , на которых
![]() .
.
Это будет в том
случае, если
![]() ;
;
![]()
![]() ;
;
б) Рассматриваем
область частот, на которых
![]() .
.
Это будет в том
случае, если
![]() ;
;
![]()
На диапазоне
частот, для которого
![]() ,
,
![]() ведет себя также, как
ведет себя также, как
![]() ,
т.е. обратная связь не влияет на систему.
,
т.е. обратная связь не влияет на систему.
2. Строим
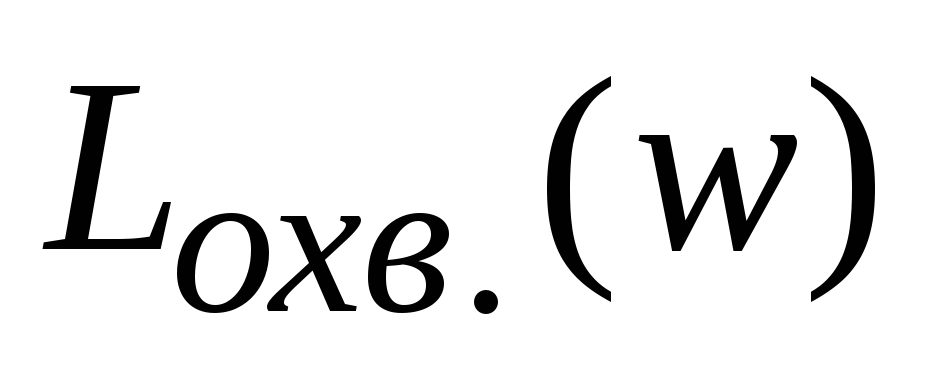 на диапазоне частот, для которых
на диапазоне частот, для которых
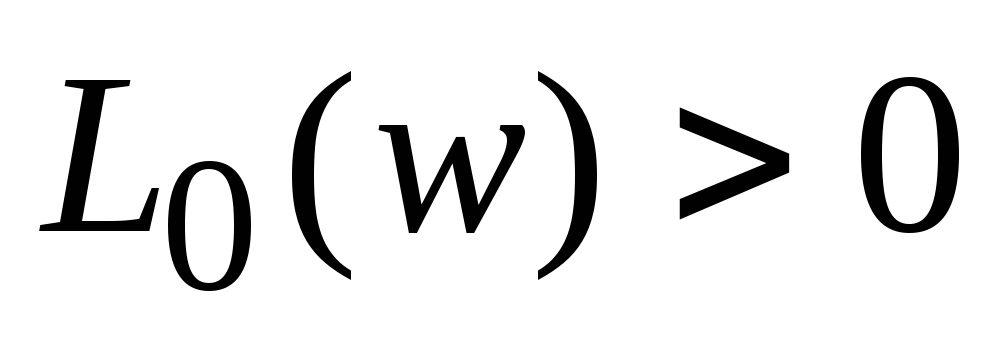 .
.3. Строим ЛАЧХ
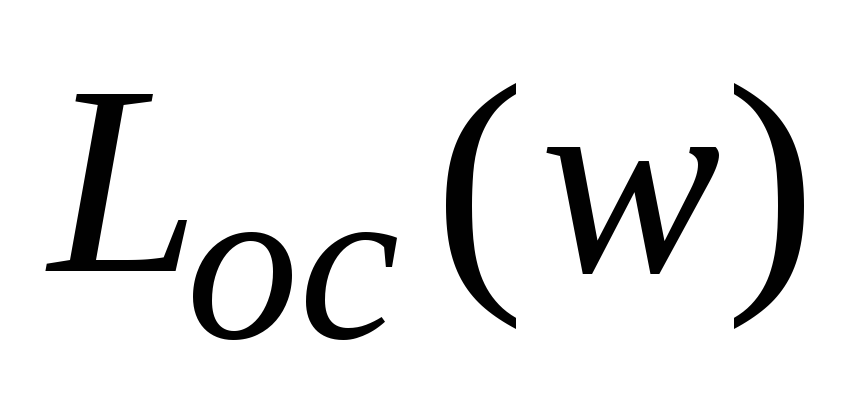 :
:
 .
.
39. Построение корректирующего устройства в цепи обратной связи на примере следящей системы.
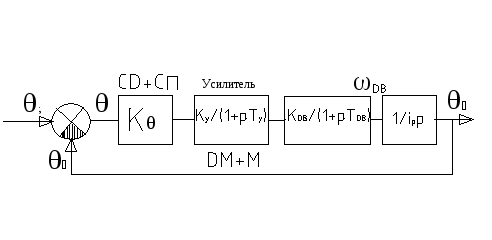 Следящая
система
Следящая
система
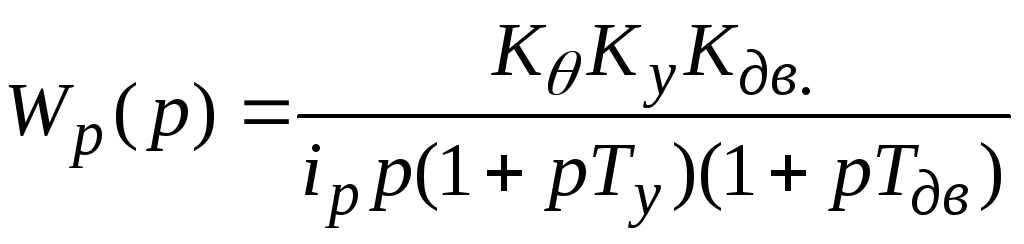 ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
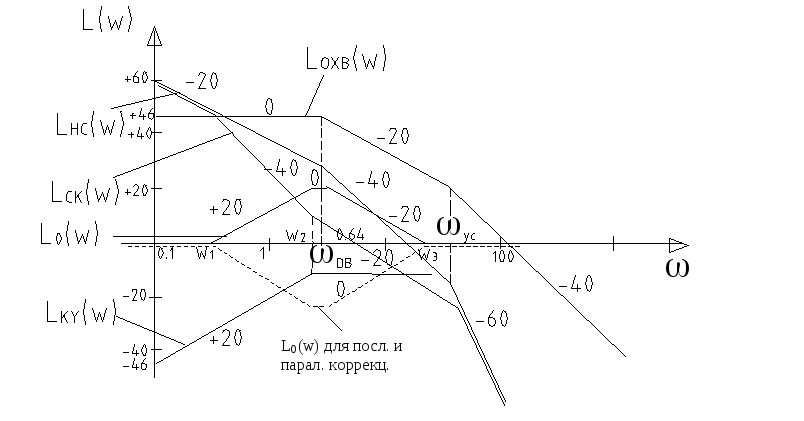
1. Построение ЛАЧХ нескорректированной системы.
![]() ;
;
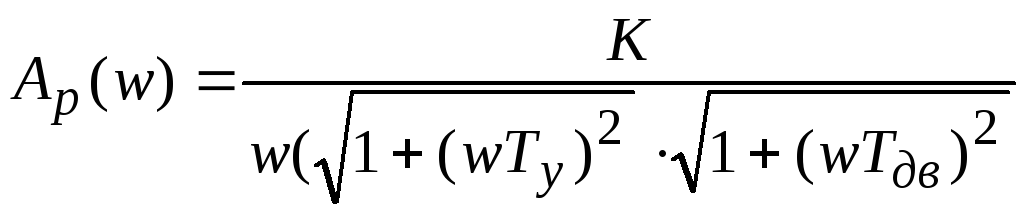 ;
;
![]() ;
;
![]() ;
;
Система
неустойчива, т.к. алгебраическая сумма
переходов
![]() через (-
через (-![]() )
приL(w)>0
равно (-1), а также запас по фазе
)
приL(w)>0
равно (-1), а также запас по фазе
![]() <0(приwср
<0(приwср
![]() ниже (-
ниже (-![]() )).(если
построить ЛФЧХ по заданному выражению-для
самостоятельной работы)
)).(если
построить ЛФЧХ по заданному выражению-для
самостоятельной работы)
Требования к системе
1.
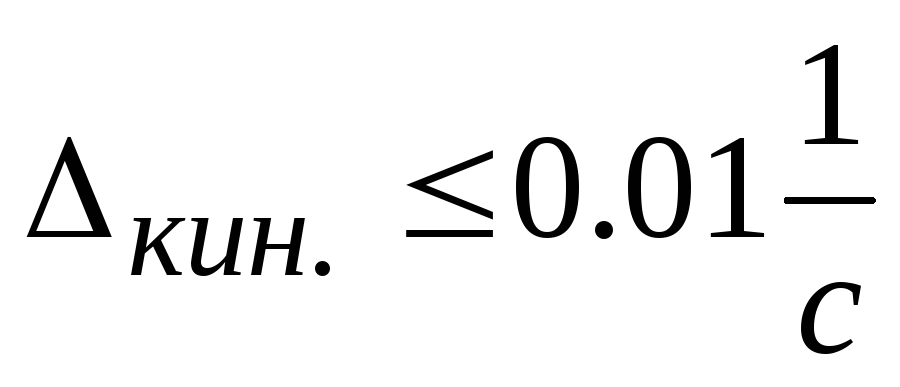 ;
;2.
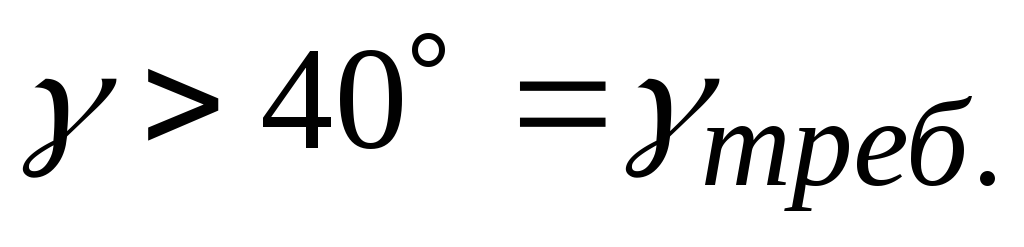 ;
;3.
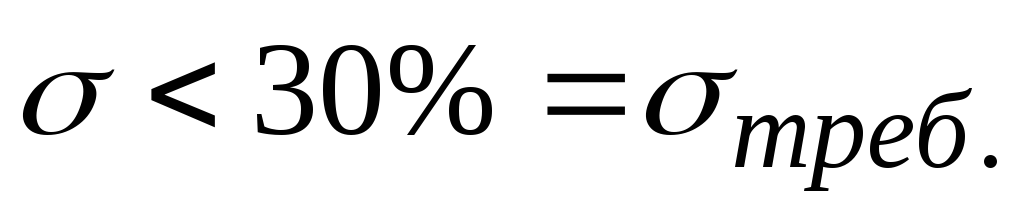 ;
;4.
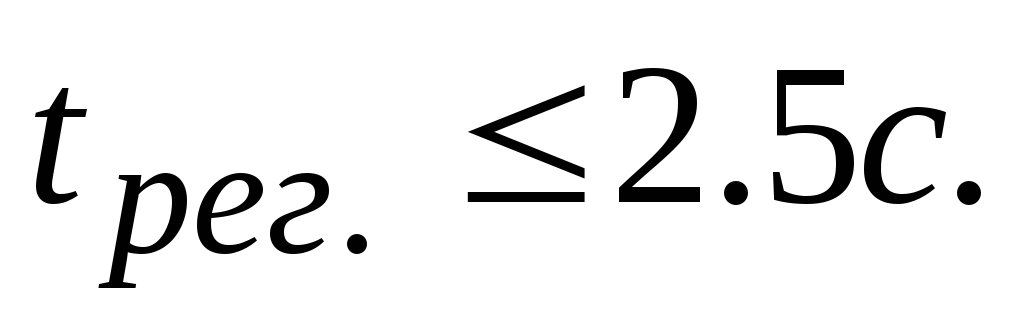 ;
;
2. Построение ЛАЧХ скорректированной системы.
![]() (используя
график из вопроса №36);
(используя
график из вопроса №36);
![]() ;
;
![]() ;
;
![]() ;
;
3. На участке, гдеL0(w)>0 строимLохв.(w).
4.
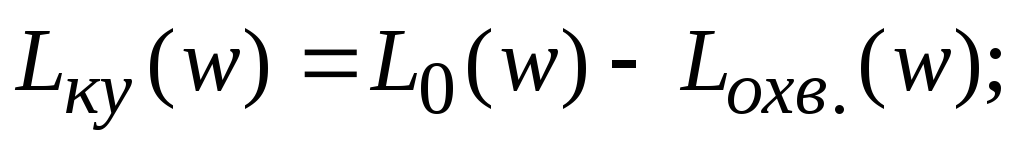
5. Передаточная функция скорректированной системы
![]() ;
(*)
;
(*)
Единицей пренебрегаем, т.к. считаем, что связь работает там, где единицей можно пренебречь. Из формулы (*) следует-охваченные звенья не влияют на скорректированную систему.
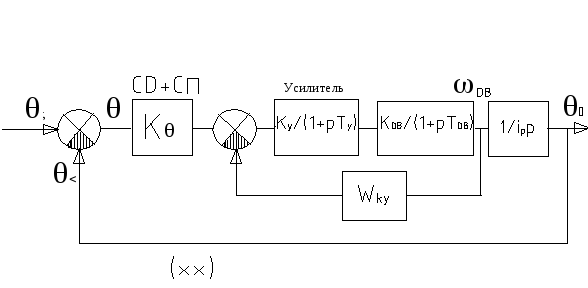 Обратной
связью охватывают звенья с нестабильными,
неустойчивыми характеристиками и с
большими постоянными времени, т.е.
инерционными.
Обратной
связью охватывают звенья с нестабильными,
неустойчивыми характеристиками и с
большими постоянными времени, т.е.
инерционными.
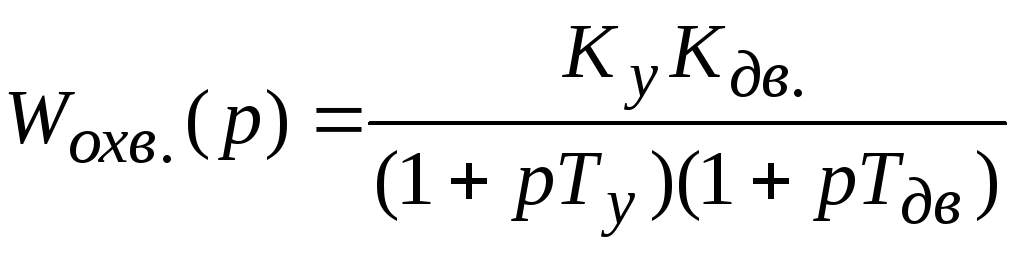 ;
;
К=100-общий коэффициент усиления;
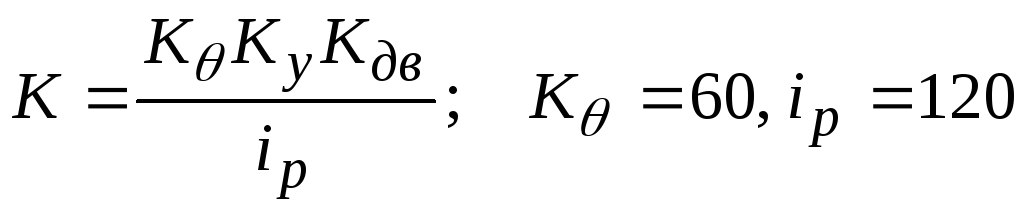
![]() ;
;
![]() ;
;
![]() ;
;
![]() -упругое
дифференцирующее звено;
-упругое
дифференцирующее звено;
![]() ;
;
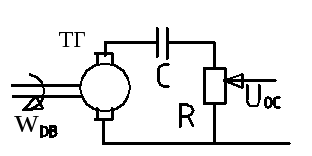
![]() ,
w>w2;
,
w>w2;
![]() -для
IIучастка;
-для
IIучастка;
Устройство для реализации схемы (**):
![]() ,
,
![]() ,
где
,
где
![]() -коэффициент
потенциометра;
-коэффициент
потенциометра;
![]()
![]()
![]() ;
;
Запас устойчивости удовлетворяет требованиям к системе, т.е. система устойчива и работает качественно.
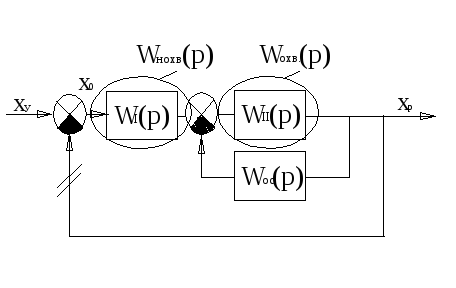
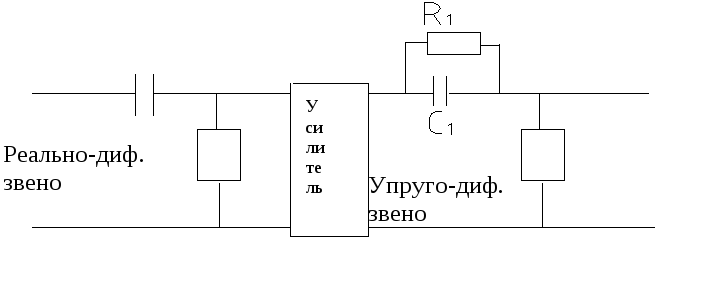
40. Построение корректирующего устройства при последовательной и параллельной коррекции на примере следящей системы.
Схему следящей системы, а также разностную ЛАЧХ смотри в вопросе №39 (пунктир).
Последовательная коррекция
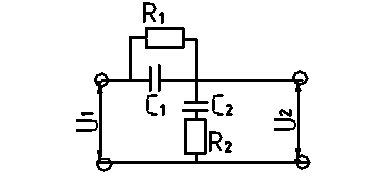
![]() ;
;
![]() ;
;
Параллельная коррекция
По
![]() восстанавливаем
восстанавливаем
![]() ;
;
![]()
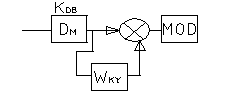 ;
;
![]() -звенья,
охваченные параллельной коррекцией;
-звенья,
охваченные параллельной коррекцией;
![]() =1;
=1;
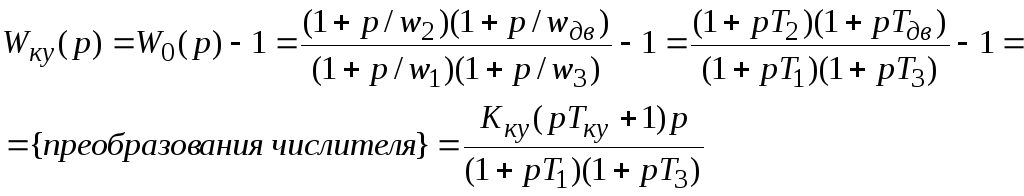
41. Дискретные системы автоматического управления. Типы дискретизации. Структурные схемы импульсных систем.
Вдискретных системах сигналы дискретны. Для дискретных сигналов характерны скачки. Для любой точки: предел слева не равен пределу справа.
Причины дискретизации:
1. Сигнал на входе дискретный.
2.
 Существует
элемент, осуществляющий дискретизацию.(ИЭ)
Существует
элемент, осуществляющий дискретизацию.(ИЭ)
Большинство систем относится к п.2.
Опр:Преобразование непрерывного сигнала в дискретный наз. квантованием.
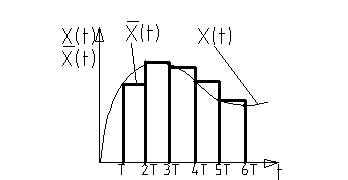
1. Квантование по времени.
Фиксируем моменты времени T1...T5и фиксируем ординаты сигнала. (Т-период квантования, интервал дискретизации).
Системы, в которых осуществляется квантование по времени, наз. импульсными системами.
Пример: кинопленка.
2.
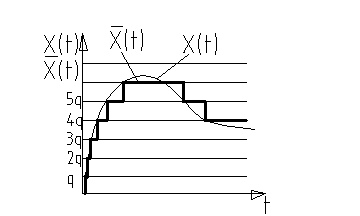 Квантование
по уровню.
Квантование
по уровню.
Фиксируем уровень(ординату), q-квант по уровню.
Системы, в которых осуществляется квантование по уровню, наз. релейными системами.(класс нелинейных систем)
Пример: цифровые весы, вольтметры, амперметры...
3.
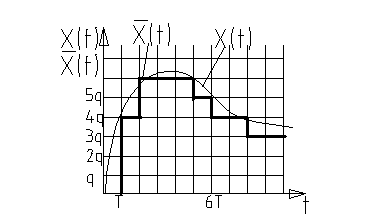 Квантование
по уровню и по времени (комбинированный).
Квантование
по уровню и по времени (комбинированный).
Округление до ближайшего кванта.
Системы в которых осуществляется квантование по уровню и по времени наз. цифровыми системами (относятся к нелинейным системам).
Пример: любая система, подключенная к ЭВМ.
Форма импульса, вырабатываемая импульсным элементом может быть разная: прямоугольная, треугольная, экспоненциальная и т.д.
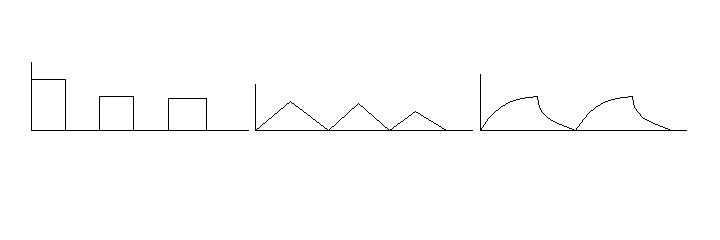
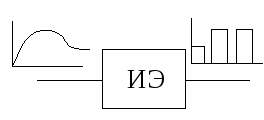
В импульсном элементе (ИЭ) вырабатывается последовательность выходных импульсов, зависящая от ординат входного сигнала в дискретные моменты времени.
Зависимость какого-либо параметра импульса от ординаты входного сигнала наз. модуляцией.
Существуют различные виды модуляций:
Амплитудно-импульсная модуляция (АИМ), зависимость от амплитуды.
Широтно-импульсная модуляция (ШИМ).
Время-импульсная модуляция.
Частотно-импульсная модуляция (ЧИМ).
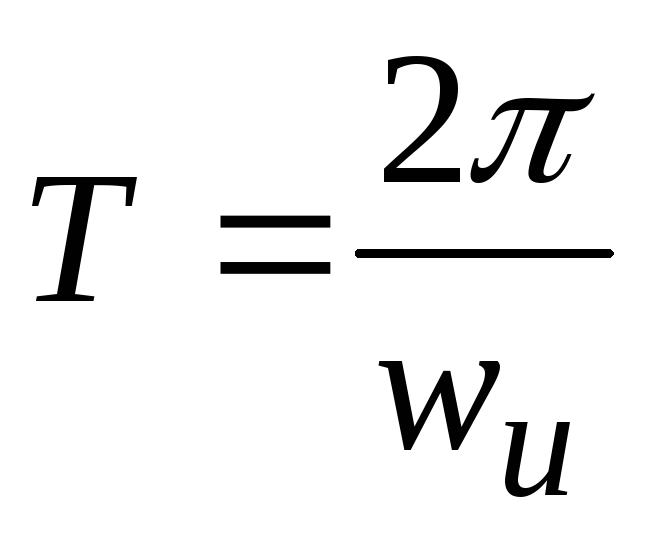 -меняется
частота следования импульсов.(чем
больше амплитуда, тем чаще идут импульсы)
-меняется
частота следования импульсов.(чем
больше амплитуда, тем чаще идут импульсы) Фазо-импульсная модуляция (ФИМ). При ФИМ меняется фаза импульса.
Мы будем рассматривать системы с АИМ-линейные импульсные системы.
Структурная схема линейных импульсных систем.
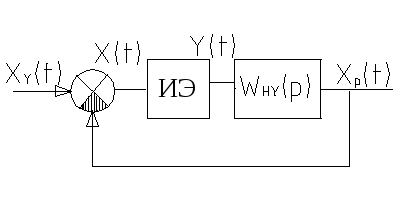
![]() -управляющий
непрерывный сигнал;
-управляющий
непрерывный сигнал;
![]() -сигнал
ошибки или отклонения (непрерывный);
-сигнал
ошибки или отклонения (непрерывный);
![]() -последовательность
импульсов на выходе импульсного элемента;
-последовательность
импульсов на выходе импульсного элемента;
![]() -регулируемый
сигнал (непрерывный);
-регулируемый
сигнал (непрерывный);
Каждый импульс
можно рассматривать, как реакцию системы
на
![]() -функцию.
-функцию.
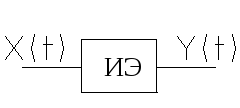
Можем заменить ИЭ идеальным импульсным элементом (ИИЭ).
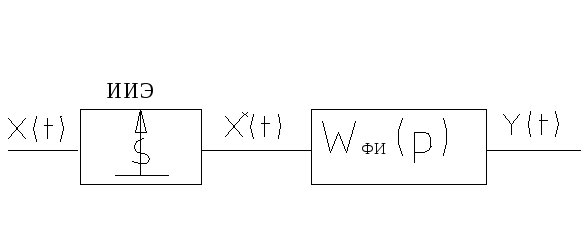
![]() -последовательность
-последовательность
![]() -функций,
модулированная ординатами входного
сигнала
-функций,
модулированная ординатами входного
сигнала
![]() в дискретные моменты времени.
в дискретные моменты времени.
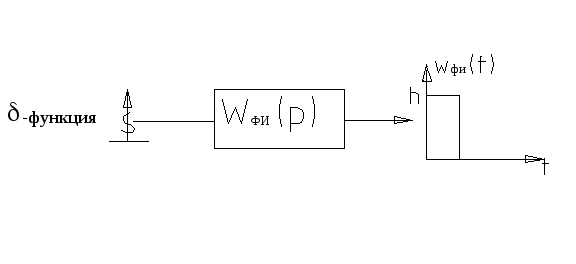
![]() -передаточная
функция формирователя импульсов (вид
зависит от формы вырвбатываемого
импульса).
-передаточная
функция формирователя импульсов (вид
зависит от формы вырвбатываемого
импульса).
Реакция системы
на
![]() -функцию
является весовая функция.
-функцию
является весовая функция.
![]() ;
;
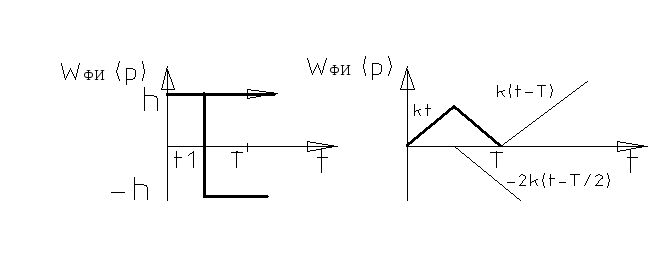
Пример определения передаточной функции Wфи(p):
Прямоугольный импульс.
![]() ;
;
Треугольный импульс.
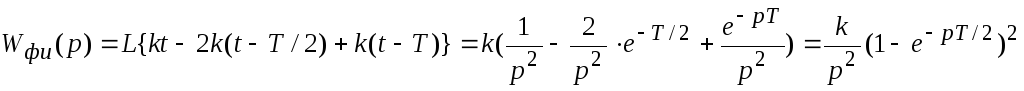 ;
;
Перерисуем структурную схему:
![]() -приведенная
непрерывная часть системы;
-приведенная
непрерывная часть системы;
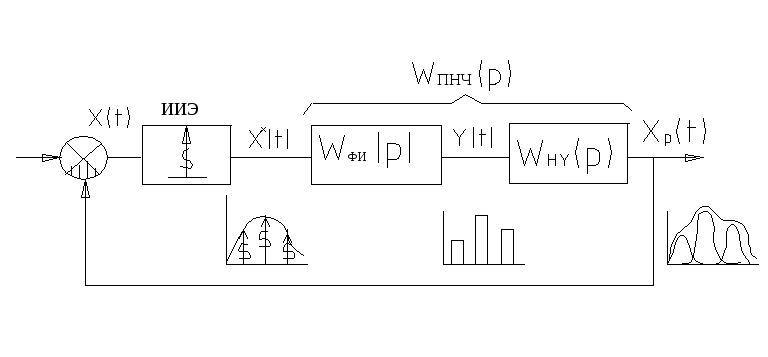
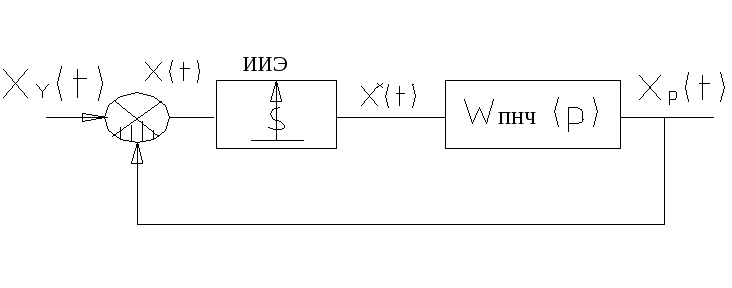 Окончательно:
Окончательно:
