10. Частотные характеристики интегрирующего и инерционного звеньев.
Интегрирующее звено:
Передаточная
функция:
где: 0 = P(
)
= Q(
)
= A(
)
j
jK
K
+
+
Построим характеристики.
1). АЧХ
Если на С подать
сигнал нулевой частоты
напряжение UCрастет до бесконечности
{речь идет видимо о схеме замещения
интегрирующего звена}.
Если
2).ФЧХ – фазо-частотная характеристика.
3). АФХ – (годограф).
j
0
+
0
4).Действительная частотная характеристика равна нулю.
Мнимая частотная
характеристика МЧХ.
5). Логарифмическая АЧХ (ЛАЧХ)
40
20lgK
20
100
1
0.1
10-
-20
Наклон 20 дб/дек,
коэффициент усиления К=
=10
6). ЛФЧХ.
0.1
10
100
Инерционное звено.
Передаточная
функция:
где: P(
)
=
Q(
)
=
А(
)
=
Перейдем к построению характеристик.
1). АЧХ (А(
)).
2). ФЧХ (
)
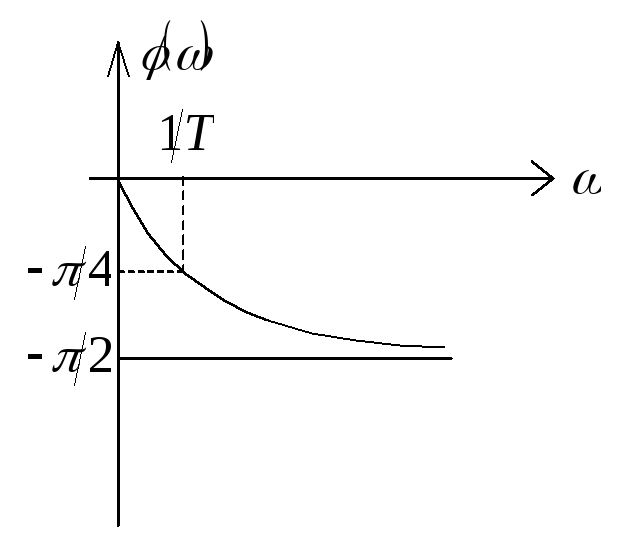
3
).
ВЧХ (Р(
))
4). МЧХ (Q(
))
5
).
АФХ (W(
))
Г
одограф
входит в 0 под углом
так как при
11. Частотные характеристики колебательного и звена запазды- вания.
Колебательное звено.
j
+
АЧХ – амплитудно-частотная характеристика
- резонансная
частота.
Рассмотрим разные
значения
ФЧХ.
П
ерейдем
к построению годографа АФХ (
)
Годограф приходит
в ноль под углом (
).
При
годограф
идет от К по оси, затем при
разрыв и входит в 0 по оси (генератор
незатухающих колебаний).
ЛАЧХ
Строится асимптотическая ЛАЧХ.
1)
2)
ЛФЧХ
Звено запаздывания
АЧХ
К
ФЧХ
- годограф
j
+
K
-
K
12. Частотные характеристики идеального и реального дифферен-
цирующих звеньев.
Пропуск.
13. Построение логарифмических частотных характеристик по пере-
даточной функции разомкнутой системы.
где:
Построение ЛАЧХ:
- асимптотическая
ЛАЧХ.
- частота сопряжения.
1).
2).
Характеристика
идет с наклоном –20 (по оси
),
при
- скачка не будет
Л
ФЧХ
14. Построение амплитудно-фазовых характеристик по передаточным
функциям разомкнутых систем.
Вопрос, конечно, поставлен хорошо, но чтобы построить АФХ необходимо, если мы не семи пядей во лбу еще построить ЛАЧХ и ЛФЧХ, что сейчас и будем делать.
Дано:
К=100; Т1= 2
с. Т2= 0.5 с. Т3= 0.02 с.
Построим логарифмические характеристики и годограф.
Запишем порядок звеньев:
0 – К.
1 -
2 -
3 -
4 -
0)
+j
K
+
1)
+j
+
1
2)
4)
+j
+
3)
Запишем выражения для амплитуды и для фазы
где
- задается (*).
К=100; Т1= 2;
Т2= 0.5; Т3= 0.02;
Строим ЛАЧХ, ЛФЧХ, АФХ.
ЛАЧХ:
0 участок:
1 –й участок:
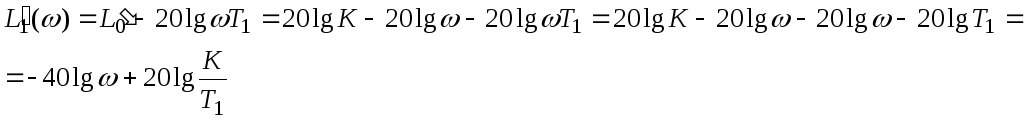
2-ой участок
3-й участок.
Л
ФЧХ
Звенья записаны по порядку следования, т.е. минус пи пополам – нулевое, следующее – первое и т.д.
Построение АФХ.
