56 . Нелинейные сау . Типовые н . Э .

Естественные Н. Э. -ограничены « энергетически ». , гистерезис , плохое исполнение .

Искусственные Н. Э. - вводятся искусственно в систему , чтобы обеспечить качественно новые процессы в системе .

 

Далее рассматриваются нелинейные системы , состоящие из нелинейного статического элемента и линейной динамической системы .

 

57 . Структурные схемы нелинейных сау . Некоторые правила их преобразования .

Линия передачи -1

Узел -2

 

 

 

 

 

 

Линейное динамическое звено -3

Нелинейный статический элемент -4

 

 

 

Три вида описания Н . Э .

1. 1)    графический

2. 2)   аналитическийf(x)=arctg(x)

3. 3)    кусочно-линейная аппроксимация

B;x>=a

f(x)= - B ; x<=a

0 ; модуль(х)<a

Соединение нелинейных статических элементов .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Особенности Н . САУ .

Принцип суперпозиции не выполняется

 

 

 

 

y=y1+y2 , для линейных систем (принцип выполняется ) ;y<>y1+y2 для нелинейных САУ .

1. 1)    в линейной части системы можно производить любые структурные преобразования .

2. 2)    нельзя переставлять Н . Э . между собой

3. 3)    нельзя переставлять линейные и Н . Э .

4. 4)    нелинейные статические элементы можно переносить через узел ветвления .

 

При переносе статического нелинейного элемента через узел по (против) направления передачи сигнала в отходящую от узла ветвь следует добавить нелинейный элемент с прямой (обратной ) характеристикой.

 

 

 

 

58 . Основные понятия фазовой плоскости , свойства фазовых траекторий . Примеры .

Исследование динамики Н . С . на фазовой плоскости .

 

 

 

 

 

 

n^гопорядка .

 

 

 

; -начальные условия .

-вектор (решение системы ) , -вектор состояния системы .

при изменении tвектор описывает траекторию вn-мерном пространстве , называемым фазовым. Дляn<=2 используют графический метод (метод фазовой плоскости ) .

n=2(плоскость ) .

 

 

 

 

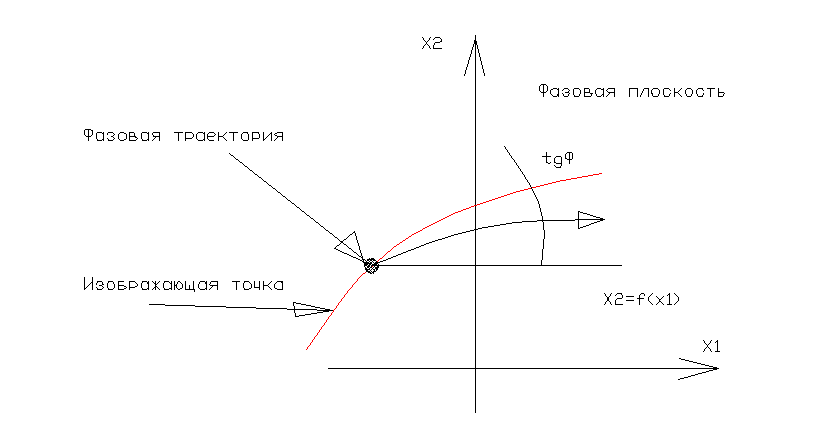
x₂=f(x₁)-изображающая точка , значение уравнения в точке .

При разных начальных значениях получается совокупность фазовых траекторий (фазовый портрет ) .

Свойства фазовых траекторий :

1. 1)    При однозначныхf₁(x₁,x₂) иf₂(x₁,x₂) - однозначная , для каждой точкиx_{1 ,}x₂ определено однозначно . Фазовые траектории не пересекаются , за исключением точек , называемых особыми .

2. 2)    Фазовые траектории заканчиваются в точках , соответствующих положениям равновесия .

, (нет движения ) . особые точки .

Нелинейная система второго порядка использует в качестве первой координаты сигнал отклонения (ошибки ) , а второй координаты - производную ,, .

3. 3)    Движение изображающий точки происходит слева направо (в верхней полуплоскости ) , а в нижней - справа налево . Изображающая точка движется по часовой стрелке .

3. 4)    Пересечение фазовыми траекториями оси абсцисс происходит под прямым углом .

, , на оси абсцисс х принимает максимальные и минимальные значения .

 

 

59 . Метод изоклин . Исследование н . Систем 2-го порядка на фазовой плоскости , типы особых точек .

Метод изоклин .

ненулевые Н . У .

; ; - уравнение фазовых траекторий .

-характеристическое уравнение системы .

 

; ;

1. 1)    ; ; ; ; ;a-tgугла наклона касательной к фазовой траектории .

; - уравнение прямых с заданным наклоном касательных к фазовой траектории =a(изоклины ) .

Изоклина -линия для которой наклон касательных к фазовой траектории постоянен .

a= 0 ,x= 0 a=¥,v= 0 a= 1 ,x= -v a= - 1 , v = x

 

2. 2)   ;

; корни комплексно сопряженные .

; ; ; ;

a= 0 ,v= -x a= - 2 ,x=v a= -1 , x = 0