Примерные варианты контрольной работы № 1 по математическому анализу

Вариант 1

1. Даны множества: , .

Для указанных множеств найти: а) , б), в).

2. а), , . Найти .

б) Решить уравнение .

3. Вычислить пределы:

.

4. Вычислить производные:

5. Исследовать функцию и построить её график.

Вариант 2

1. Даны множества: , .

Для указанных множеств найти: а) , б), в).

2. а) Найти

б) Решить уравнение

3. Вычислить пределы:

4. Вычислить производные:

5. Исследовать функцию и построить её график.

6. Неопределённый интеграл Первообразная. Неопределённый интеграл

Функция F(x), определённая и дифференцируемая на отрезке , называется первообразной для функции f(x), если выполняется равенство .

Если функция f(x) имеет первообразную F(х), то все функции вида F(x)+C также являются первообразными для f(x), где С = const.

f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.

Теорема. Если F(x) и G(x) – две любые первообразные для f(x), то они могут различаться лишь на постоянное слагаемое, т.е. .

Совокупность всех первообразных для данной функции f(x) называется неопределённым интегралом от этой функции и обозначается , где С – произвольная постоянная.

Действия дифференцирования и интегрирования взаимно обратны:

Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции:

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого:

4. Постоянный множитель можно выносить за знак неопределенного интеграла:

5. Неопределенный интеграл от алгебраической суммы ко­нечного числа непрерывных функций равен сумме неопределен­ных интегралов от этих функций:

6. Если , то , где a, b – постоянные числа, а ≠ 0.

7. Если , то , где - любая дифференцируемая функция.

Таблица неопределённых интегралов

1., n ≠ -1 2. 3. 4. 5. , а > 0, а ≠ -1 6. 7. 8. 9. 10.

11. 12. 13. 14. 15. 16. 17. 18. , n ≠ -1, k ≠ 0 19. 20.

Основные методы интегрирования Метод разложения

Пусть , тогда на основании свойства неопределенного интеграла: .

Примеры:

Найти интегралы:

1.

При решении данного примера использовались свойства неопределённого интеграла: вынесение постоянного множителя за знак интеграла, разделение суммы функций, стоящих под знаком интеграла, на несколько интегралов, значения которых являются табличными.

2. .

3. .

4.

.

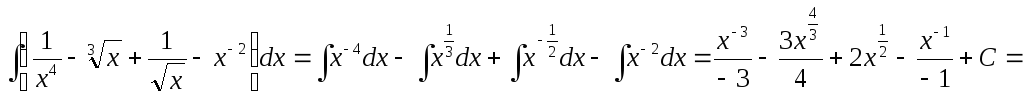
5. .

6. .