Наибольшее и наименьшее значения функции

Для нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a,b], нужно найти значения функции на концах отрезка и в критических точках, принадлежащих этому отрезку, затем выбрать из этих значений наибольшее и наименьшее.

Пример 3. Найти наибольшее и наименьшее значения функции на отрезке .

Решение.

Находим значение функции в критических точках и на концах отрезка. Заметим, что значение , поэтому значение функции при находить не нужно.

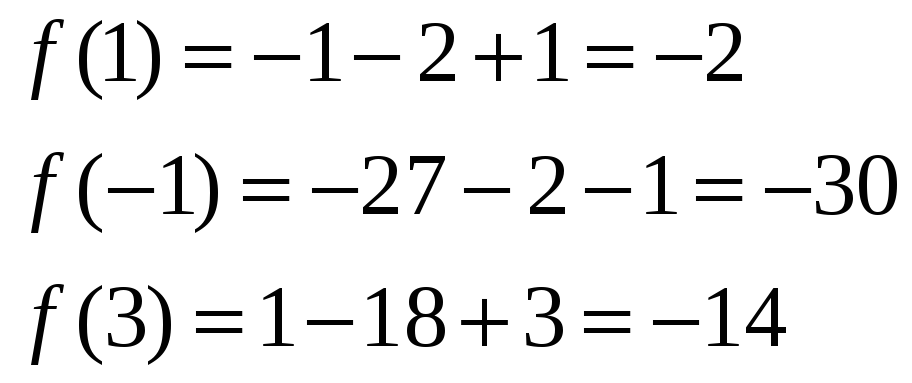
Наибольшее значение , наименьшее .

Правила Лопиталя для раскрытия неопределенностей

1. Если то при условии, что предел в правой части равенства существует.

2. Если то при условии, что предел в правой части равенства существует.

Эти правила можно распространить и на случай, когда

Если или то правила Лопиталя можно применять ещё несколько раз, пока неопределённость не будет раскрыта.

Примеры. Вычислить пределы:

1. .

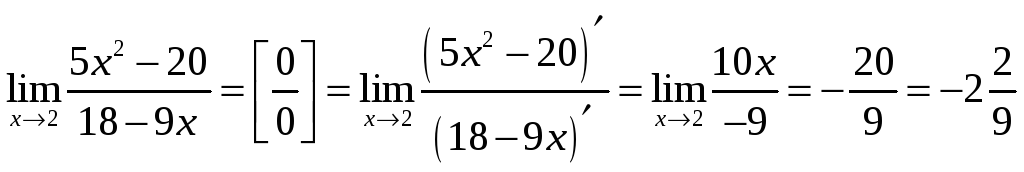2. .

Выпуклость, вогнутость и точки перегиба графика функции

График функции y = f(x) называется выпуклым (вверх) на интервале (a,b), если на этом интервале кривая f(x) лежит ниже касательной к графику функции, проведенной в любой точке интервала (a,b), и называется вогнутым (выпуклым вниз), если f(x) лежит выше касательной к графику функции в любой точке этого интервала.

Если функция y = f(x) в каждой точке интервала (a,b) имеет вторую производную то график функции имеет на интервале (a,b) выпуклость вверх (вниз).

Точка графика функции y = f(x), в которой кривая f(x) меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.

Достаточное условие точки перегиба.

Пусть функция y = f(x) имеет вторую производную в окрестности точки в которой или не существует. Тогда, если при переходе через точку слева направо меняет знак с плюса на минус (с минуса на плюс), то - точка перегиба графика функции f(x).

Алгоритм исследования функции на выпуклость и вогнутость похож на алгоритм исследования её на возрастание и убывание, но вместо знаков рассматривают знаки

Пример 4. Исследовать на выпуклость и вогнутость и найти точки перегиба графика функции

Решение.

1. Область определения функции – интервал

2.

3.

4. при x = 0.

5.

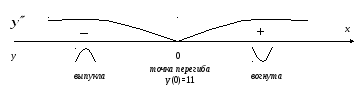
При x < 0 следовательно, функция выпукла при

При x > 0 следовательно, функция вогнута на

x = 0 – точка перегиба; y(0) = 11.

Пример 5. Исследовать на выпуклость и вогнутость и найти точки перегиба графика функции

Решение.

1. Область определения функции

2.

3.

4. Вторая производная не существует в точке х = ½, но в этой точке не существует также и функция у.

5.

При x < ½ функция выпукла, при x > ½ функция вогнута.

Асимптоты графика функции

Прямая, к которой неограниченно приближается график функции при или , называется асимптотой.

Если хотя бы один из пределов или то прямая x = a является вертикальной асимптотой. Здесь x = a является точкой разрыва функции. Непрерывные функции не имеют вертикальных асимптот.

Прямая y = kx + b является наклонной асимптотой графика функции y = f(x), если существуют пределы:

Если или то прямая y = b является горизонтальной асимптотой графика функции f(x).

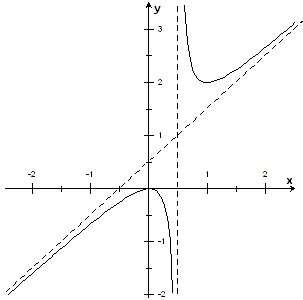
Пример 6. Найти асимптоты кривой

Решение. 1) Функция у не определена при х = ½. Это точка разрыва функции. Находим пределы функции слева и справа в этой точке.

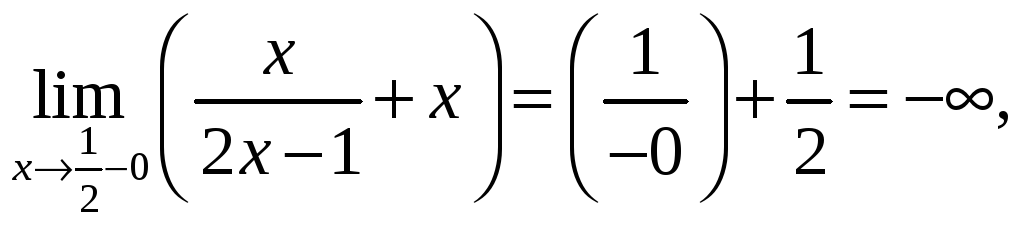
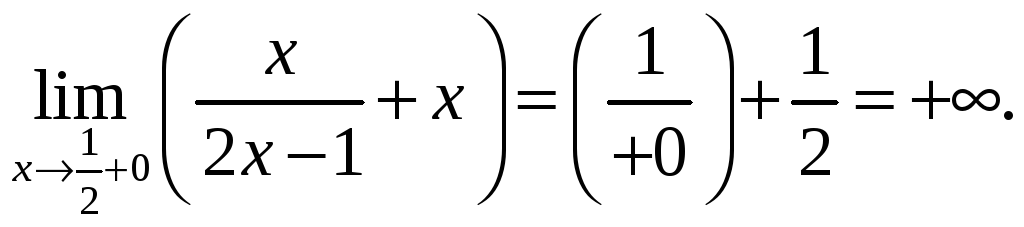
Значит, - вертикальная асимптота.

2) Находим наклонную асимптоту y = kx + b. Вычислим k и b:

Следовательно, - наклонная асимптота.

Пример 7. Найти асимптоты графика функции .

Решение. 1) Функция y не определена при

- вертикальная асимптота.

2)

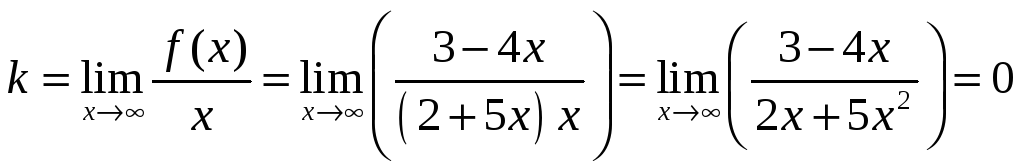
- горизонтальная асимптота.