
- •Комплексные числа
- •Операции над комплексными числами
- •2. Числовые последовательности
- •3. Понятие функции. Предел и непрерывность функции
- •Методы раскрытия неопределённостей при вычислении пределов функций
- •Эквивалентные бесконечно малые величины
- •Непрерывность функции. Классификация точек разрыва
- •Классификация точек разрыва
- •4. Производная и дифференциал функции
- •Правила дифференцирования
- •Дифференциал функции
- •Производные высших порядков
- •Применение производной в экономике. Эластичность функции
- •5. Применение производной к исследованию функций Возрастание и убывание функций. Локальный экстремум функции
- •Наибольшее и наименьшее значения функции
- •Правила Лопиталя для раскрытия неопределенностей
- •Выпуклость, вогнутость и точки перегиба графика функции
- •Асимптоты графика функции
- •Исследование функций и построение графиков
- •Примерные варианты контрольной работы № 1 по математическому анализу
- •6. Неопределённый интеграл Первообразная. Неопределённый интеграл
- •Основные методы интегрирования Метод разложения
- •Метод замены переменной. Подведение под знак дифференциала
- •Метод интегрирования по частям
- •Интегрирование дробно-рациональных выражений
- •Метод неопределённых коэффициентов
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
МИНИСТЕРСТВО ФИНАНСОВ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВСЕРОССИЙСКАЯ ГОСУДАРСТВЕННАЯ НАЛОГОВАЯ АКАДЕМИЯ
Математика. Практикум по математическому анализу
Методические рекомендации
Москва – 2010
Автор
Мамонтова Н.В.
Рецензент
Утверждено и рекомендовано
УМС финансово-экономического факультета ВГНА Минфина России
в качестве учебно-методического издания
ВГНА Минфина России, 2010
Мамонтова Н.В., 2010
Математический анализ
1. Числовые множества
Под множеством понимается совокупность (набор) некоторых объектов. Объекты, которые образуют множество, называются элементами этого множества.
Множества
обозначаются прописными буквами, а их
элементы – строчными. Если а
– элемент множества А,
то используется обозначение
![]() .
Если b
не является элементом множества А,
то пишут
.
Если b
не является элементом множества А,
то пишут
![]() .
.
Множество,
не содержащее ни одного элемента,
называется пустым и обозначается
![]() .
.
Если
множество В
состоит из части элементов множества
А
или совпадает с ним, то множество В
называется подмножеством множества А
и обозначается
![]() .
Два множества называются равными,
если они состоят из одних и тех же
элементов.
.
Два множества называются равными,
если они состоят из одних и тех же
элементов.
Объединением
двух множеств А
и В
называется множество С,
состоящее из всех элементов, принадлежащих
хотя бы одному из данных множеств,
![]() .
.
Пересечением
двух множеств А
и В
называется множество D,
состоящее из всех элементов, одновременно
принадлежащих каждому из данных множеств
А
и В,
![]() .
.
Разностью
множеств А
и В
называется множество Е,
состоящее из всех элементов множества
А,
которые не принадлежат множеству В,
![]() .
.
На диаграммах Эйлера – Венна:

Пример
1. Даны
множества
![]() ,
,
![]() .
Найти
.
Найти
![]() .
.
Решение.
Изобразим множества А и В на числовых осях:

Объединение
![]() - числа, которые входят и в множество А
и в множество В.
- числа, которые входят и в множество А
и в множество В.
Разность
![]() - числа, которые входят только в множество
А,
но не входят в В.
- числа, которые входят только в множество
А,
но не входят в В.
Разность
![]() - числа, которые входят только в множество
В,
но не входят в А.
- числа, которые входят только в множество
В,
но не входят в А.
Пересечение
![]() - числа, которые входят как в множество
А,
так и в В.
- числа, которые входят как в множество
А,
так и в В.
Пример
2. Даны
множества
![]() ,
,
![]() .
Найти
.
Найти
![]() .
.
Решение.

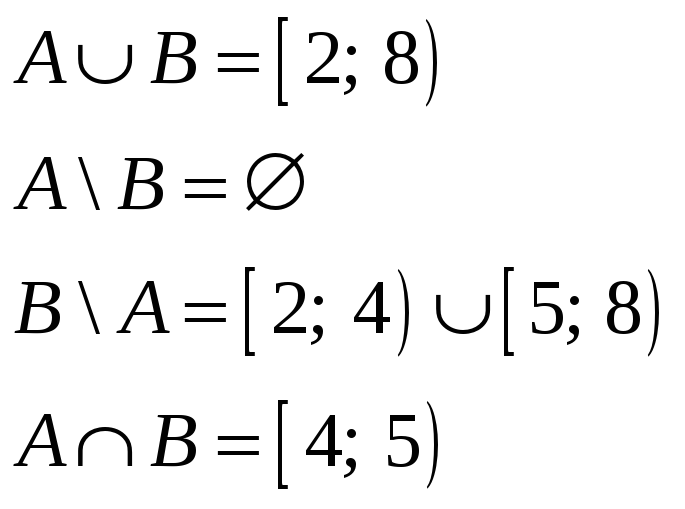
Пример
3. Даны
множества
![]() ,
,
![]() .
Найти
.
Найти
![]() .
.
Решение.

Комплексные числа
Комплексным
числом
называется выражение вида z
= a + bi,
где a и b
– любые действительные числа, i
– число, которое называется мнимой
единицей,
![]()
![]() .
.
Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.
Числа a + bi и a – bi называются сопряжёнными; числа a + bi и – a – bi – противоположными.
Операции над комплексными числами
Пусть
![]() ,
,
![]() .
.
1.
![]()
2.
![]()
3.
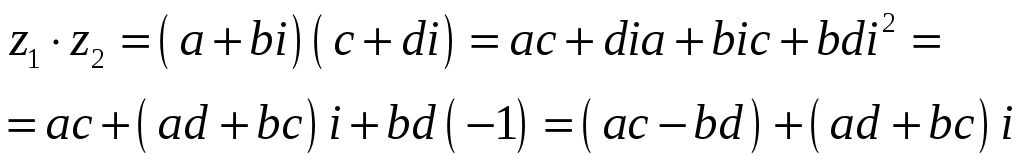
4.
![]()
Пример
4. Даны
комплексные числа
![]() .
Найти
.
Найти
![]() .
.
Решение.

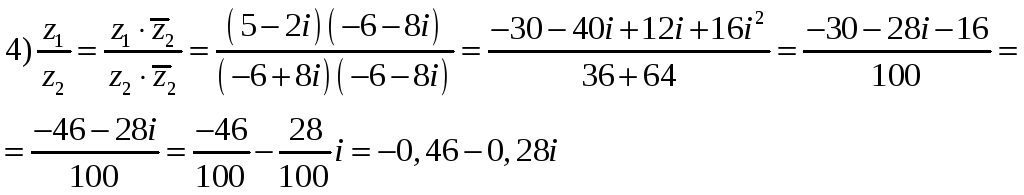
Пример
5. Решить
уравнение
![]() .
.
Решение. Действительных корней нет, но существуют комплексные корни уравнения.
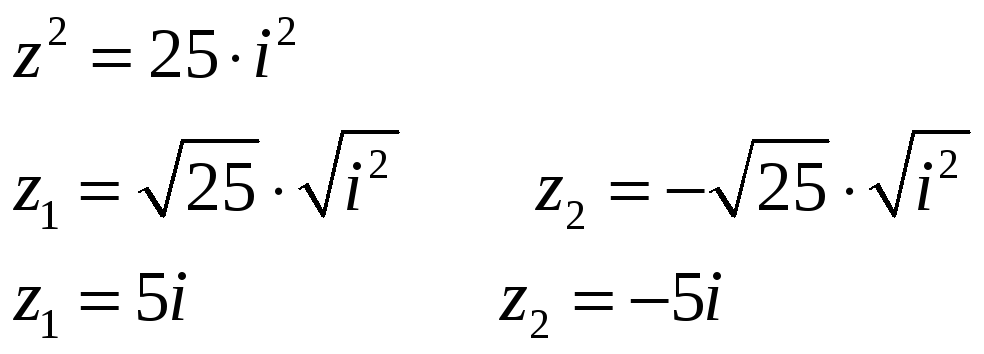
Пример
6. Решить
уравнение
![]() .
.
Решение.
![]() .
.

Задания для самостоятельного решения:
-
Даны множества
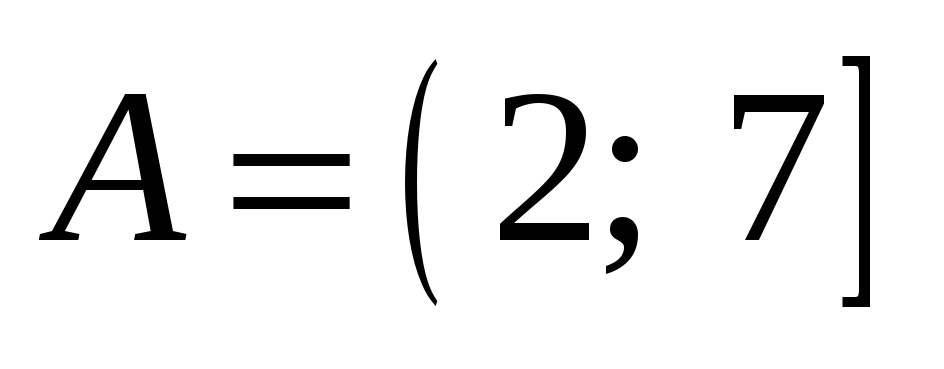 ,
,
 .
Найти
.
Найти
 .
. -
Даны множества
 ,
,
 .
Найти
.
Найти
 .
. -
Даны множества
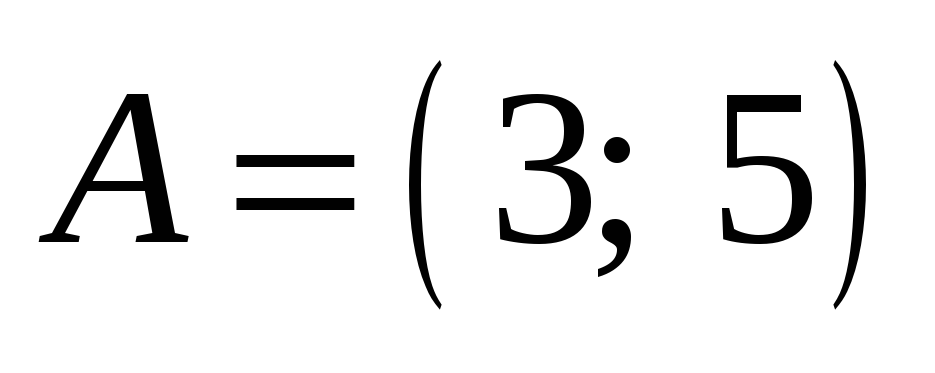 ,
,
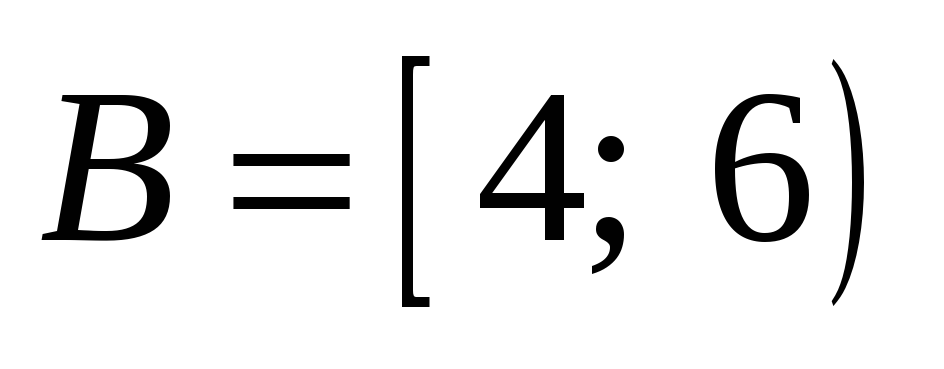 ,
где х
– натуральное число.
,
где х
– натуральное число.
Найти
![]() .
.
-
Даны множества
 ,
,
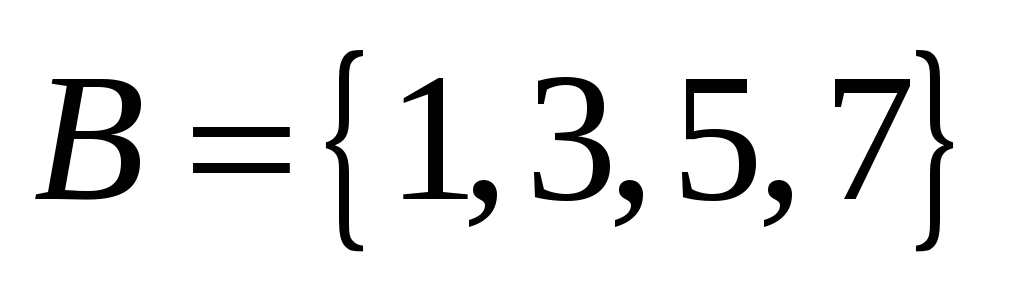 .
Найти
.
Найти
 .
.
5.
Даны комплексные числа
![]() и
и
![]() .
Найти
.
Найти
![]() .
.
6.
Даны комплексные числа
![]() ,
,![]() ,
,
![]() .
Найти
.
Найти
![]() .
.
7.
Решить уравнение
![]() .
.
8.
Решить уравнение
![]() .
.
9.
Решить уравнение
![]() .
.
2. Числовые последовательности
Если
по некоторому закону каждому натуральному
числу n
поставлено в соответствие определённое
число
![]() ,
то говорят, что задана числовая
последовательность
,
то говорят, что задана числовая
последовательность
![]() :
:
![]() .
Можно сказать, что числовая последовательность
– это функция натурального аргумента
.
Можно сказать, что числовая последовательность
– это функция натурального аргумента
![]() .
Числа
.
Числа
![]() называются членами
последовательности, а число
называются членами
последовательности, а число
![]() - общим или n-ным
членом
последовательности.
- общим или n-ным
членом
последовательности.
Число
А
называется пределом
числовой последовательности
![]() ,
если для любого, даже сколь угодно малого
положительного числа
,
если для любого, даже сколь угодно малого
положительного числа
![]() ,
найдётся номер N
(зависящий от ε,
N
= N(ε)),
что для всех членов последовательности
с номерами
,
найдётся номер N
(зависящий от ε,
N
= N(ε)),
что для всех членов последовательности
с номерами
![]() верно неравенство
верно неравенство
![]() .
Обозначается
.
Обозначается
![]() .
.
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящийся.
Последовательность
![]() называется бесконечно
малой, если
называется бесконечно
малой, если
![]()
Последовательность
![]() называется бесконечно
большой,
если для любого числа М
> 0 существует
номер N
= N(M)
такой, что при n
> N
выполняется неравенство
называется бесконечно
большой,
если для любого числа М
> 0 существует
номер N
= N(M)
такой, что при n
> N
выполняется неравенство
![]() Обозначается
Обозначается
![]()
Если
при этом, начиная с некоторого номера,
все члены
![]()
![]() то пишут
то пишут
![]()
![]()
Свойства бесконечно малых.
1. Сумма конечного числа бесконечно малых является бесконечно малой.
2. Произведение бесконечно малой на ограниченную величину (в частности на бесконечно малую) является бесконечно малой.
Величина,
обратная бесконечно малой, является
бесконечно большой, то есть
![]() бесконечно большая, если
бесконечно большая, если
![]() бесконечно
малая.
бесконечно
малая.
Величина, обратная бесконечно большой, является бесконечно малой.
Суммой,
произведением и частным последовательностей
![]() и
и
![]() называется последовательности
называется последовательности
![]() вида
вида
![]()
![]()
![]() n
= 1, 2, … .
n
= 1, 2, … .
Если
последовательности
![]() и
и
![]() имеют конечные пределы
имеют конечные пределы
![]()
![]() то последовательности
то последовательности
![]() имеют пределы a
+ b,
ab,
имеют пределы a
+ b,
ab,
![]()
![]() соответственно.
соответственно.
В
случае, когда последовательности
![]() и
и
![]() являются бесконечно большими или
бесконечно малыми, возникают
неопределенности типа
являются бесконечно большими или
бесконечно малыми, возникают
неопределенности типа
![]()
![]() отношения бесконечно малых или бесконечно
больших, а также типа
отношения бесконечно малых или бесконечно
больших, а также типа
![]()
![]() разность бесконечно больших и произведение
бесконечно малой на бесконечно большую
или некоторые другие более сложные типы
неопределенностей.
разность бесконечно больших и произведение
бесконечно малой на бесконечно большую
или некоторые другие более сложные типы
неопределенностей.
Пример
1. Найти
предел последовательности
![]()
Решение.
При подстановке
∞ вместо n,
получаем неопределенность
![]() Разделим числитель и знаменатель дроби
на
Разделим числитель и знаменатель дроби
на
![]() (наивысшая степень n).
(наивысшая степень n).
По теоремам о пределах, используя связь между бесконечно малыми и бесконечно большими величинами, получим:

![]() бесконечно малые величины).
бесконечно малые величины).
Пример
2. Найти
предел последовательности
![]()
Решение.
При подстановке ∞ вместо n,
получаем неопределенность
![]() Умножим и разделим выражение в скобках
на сопряжённое и перейдем к пределу:
Умножим и разделим выражение в скобках
на сопряжённое и перейдем к пределу:
![]()
![]()
Пример
3. Найти
предел последовательности
![]()
Решение.
При подстановке ∞ вместо n,
получаем неопределенность
![]() Разделим числитель и знаменатель дроби
на n:
Разделим числитель и знаменатель дроби
на n:

Пример
4. Найти
предел последовательности
 .
.
Решение.
При подстановке ∞ вместо n,
получаем неопределенность
![]() Вынесем за скобки в числителе и в
знаменателе члены, содержащие переменную:
Вынесем за скобки в числителе и в
знаменателе члены, содержащие переменную:
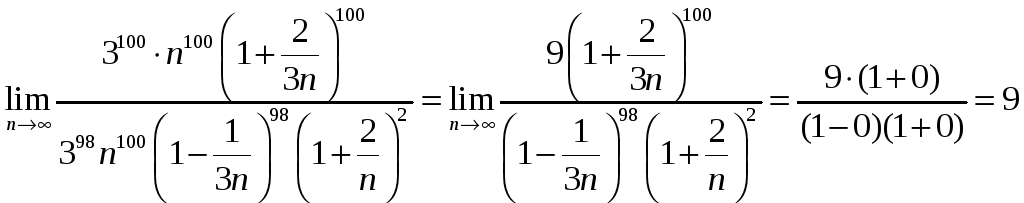 .
.
Задания для самостоятельного решения:
Найти пределы последовательностей:
-
 .
. -
 .
. -
 .
. -
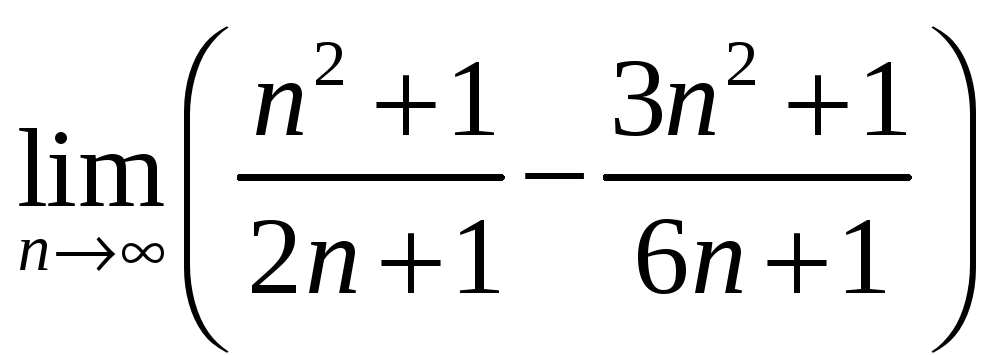 .
.
-

-
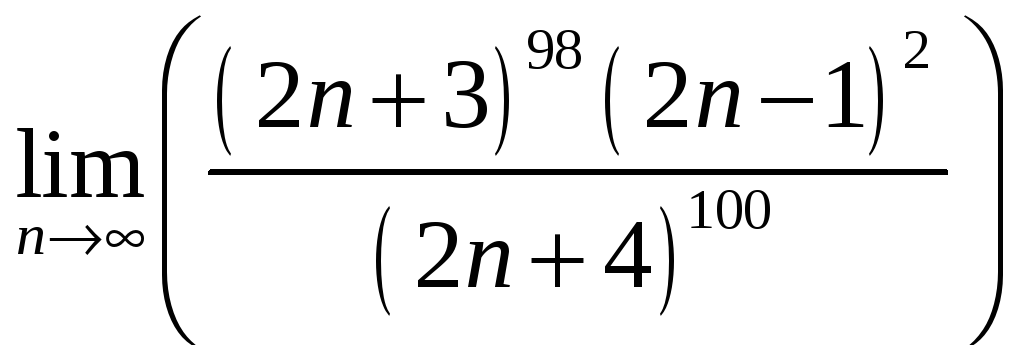 .
. -
 .
. -
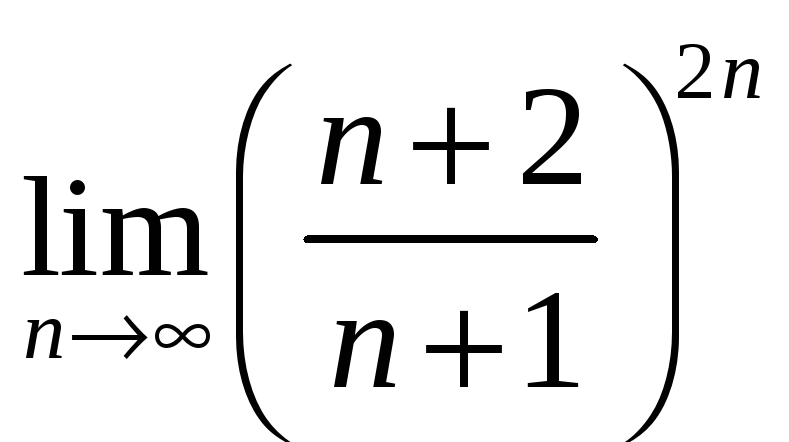 .
.
