
- •Комплексные числа
- •Операции над комплексными числами
- •2. Числовые последовательности
- •3. Понятие функции. Предел и непрерывность функции
- •Методы раскрытия неопределённостей при вычислении пределов функций
- •Эквивалентные бесконечно малые величины
- •Непрерывность функции. Классификация точек разрыва
- •Классификация точек разрыва
- •4. Производная и дифференциал функции
- •Правила дифференцирования
- •Дифференциал функции
- •Производные высших порядков
- •Применение производной в экономике. Эластичность функции
- •5. Применение производной к исследованию функций Возрастание и убывание функций. Локальный экстремум функции
- •Наибольшее и наименьшее значения функции
- •Правила Лопиталя для раскрытия неопределенностей
- •Выпуклость, вогнутость и точки перегиба графика функции
- •Асимптоты графика функции
- •Исследование функций и построение графиков
- •Примерные варианты контрольной работы № 1 по математическому анализу
- •6. Неопределённый интеграл Первообразная. Неопределённый интеграл
- •Основные методы интегрирования Метод разложения
- •Метод замены переменной. Подведение под знак дифференциала
- •Метод интегрирования по частям
- •Интегрирование дробно-рациональных выражений
- •Метод неопределённых коэффициентов
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
Интегрирование иррациональных функций
1. Дробно-линейные иррациональности
а)
Под дробно-линейной иррациональностью
понимается выражение вида
![]() .
Пусть необходимо вычислить
.
Пусть необходимо вычислить
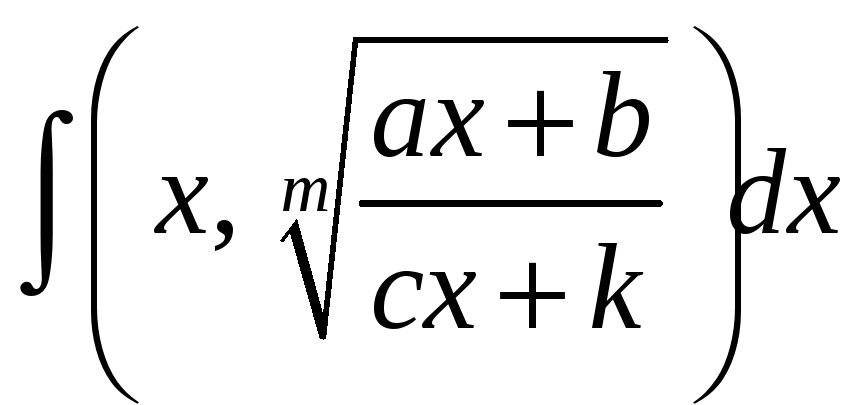 (*),
где R
– рациональная функция от х
и от
(*),
где R
– рациональная функция от х
и от
![]() .
Интегрирование таких выражений
осуществляется с помощью замены
.
Интегрирование таких выражений
осуществляется с помощью замены
![]() .
.
Тогда
![]() .
.
Подставив
![]() в интеграл (*), получим:
в интеграл (*), получим:
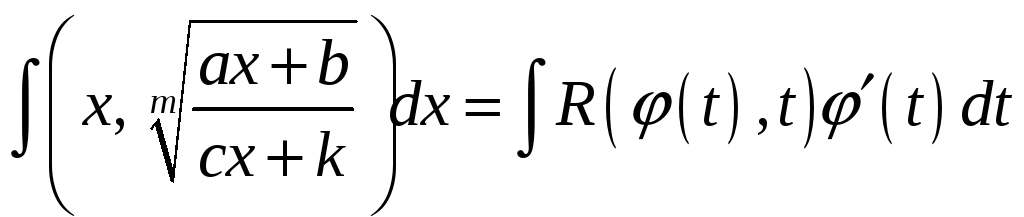 .
Такой интеграл является интегралом от
рациональной функции.
.
Такой интеграл является интегралом от
рациональной функции.
б)
Пусть в подынтегральной функции в
качестве аргументов имеются радикалы
с одним и тем же подкоренным выражением,
но с разными степенями:
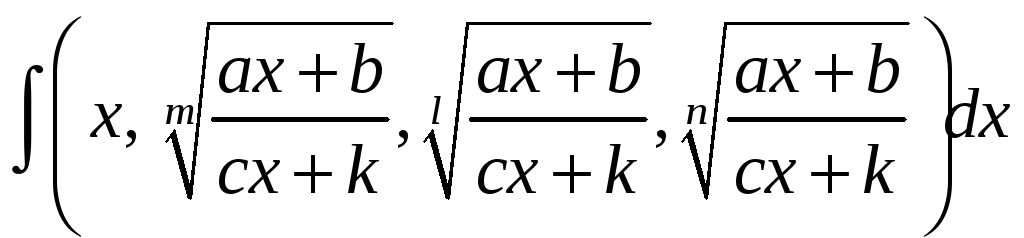 (**)
(**)
Вычисление
интегралов с такой функцией проводится
следующим образом. Пусть для степеней
m,
l,
n
число s
является наименьшим общим кратным,
тогда отношения
![]() являются также натуральными числами.
Вводится замена
являются также натуральными числами.
Вводится замена
![]() .
Тогда
.
Тогда
![]() .
С учётом этих замен подынтегральная
функция (**) от новой переменной является
рациональной алгебраической функцией.
.
С учётом этих замен подынтегральная
функция (**) от новой переменной является
рациональной алгебраической функцией.
Пример.
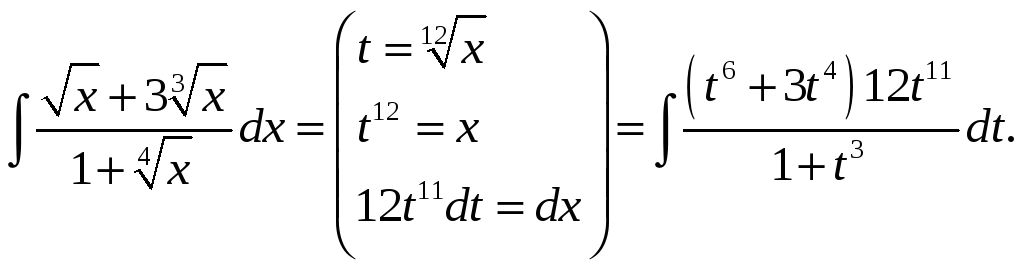
2. Квадратичные иррациональности
а)
Выражение вида
![]() называется квадратичной иррациональностью.
Пусть необходимо вычислить
называется квадратичной иррациональностью.
Пусть необходимо вычислить
![]() (*),
где
(*),
где
![]() - рациональная функция от аргументов х
и
- рациональная функция от аргументов х
и
![]() .
.
Для решения таких интегралов используются подстановки Эйлера.
1)
Пусть в иррациональности
![]() ,
тогда используется подстановка
,
тогда используется подстановка
![]() .
.
![]()
![]()
Подставляя
это в (*), окончательно получим:
![]() .
.
2)
Пусть в иррациональности
![]() ,
тогда используется подстановка
,
тогда используется подстановка
![]() .
.
![]() .
.
Подставляя это в (*), получим рациональное подынтегральное выражение.
3)
Пусть
![]() имеет различные действительные корни
λ
и μ.
Тогда
имеет различные действительные корни
λ
и μ.
Тогда
![]() примет вид
примет вид
![]() .
Используется третья подстановка Эйлера:
.
Используется третья подстановка Эйлера:
![]() .
Возведя в квадрат и сократив на
.
Возведя в квадрат и сократив на
![]() ,
получим
,
получим
![]() - это дробно-линейная подстановка,
исследуемая в пункте 1.
- это дробно-линейная подстановка,
исследуемая в пункте 1.
б) Часто подстановки Эйлера приводят к громоздким вычислениям, поэтому можно использовать тригонометрические подстановки.
1)
Пусть в иррациональности
![]() .
Выделим в подкоренном выражении
.
Выделим в подкоренном выражении
![]() полный квадрат:
полный квадрат:
 ,
где
,
где
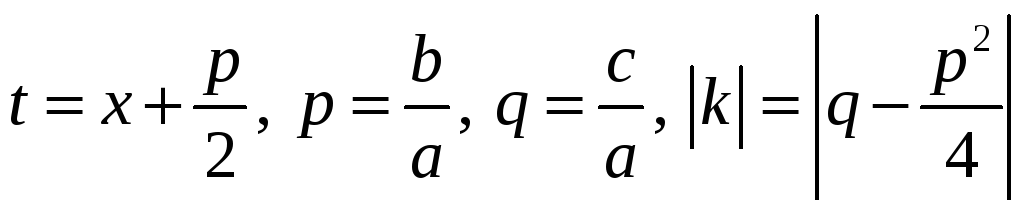 .
.
-
Для выражения
![]() используется подстановка
используется подстановка
![]() .
Получим:
.
Получим:
![]() .
.
-
Для выражения
![]() используется подстановка
используется подстановка
![]() .
.
![]() .
.
2)
Пусть в иррациональности
![]() ,
тогда
,
тогда
![]()
![]() .
.
![]()
Итак,
если после выделения полного квадрата
и введения переменной t
получим
![]() ,
то используется подстановка
,
то используется подстановка
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Интегрирование тригонометрических функций
Рассмотрим
интеграл вида
![]() ,
где R
–рациональная функция от sin
x
и от cos
x.
Общим методом интегрирования таких
тригонометрических функций является
метод
универсальной тригонометрической
подстановки
вида
,
где R
–рациональная функция от sin
x
и от cos
x.
Общим методом интегрирования таких
тригонометрических функций является
метод
универсальной тригонометрической
подстановки
вида
![]() .
При этом тригонометрическая подынтегральная
функция переходит в дробно-рациональную
функцию.
.
При этом тригонометрическая подынтегральная
функция переходит в дробно-рациональную
функцию.
 .
.
Пример
1.
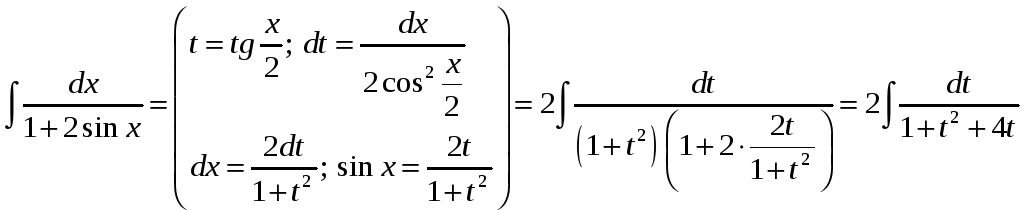 .
.
Данный интеграл можно найти, используя метод неопределённых коэффициентов.
Применение универсальной подстановки часто приводит к громоздким вычислениям, поэтому при возможности используют более простые приёмы.
1.
Функция
![]() нечётна относительно sin
x,
если выполняется равенство
нечётна относительно sin
x,
если выполняется равенство
![]() .
В таких случаях используется замена
.
В таких случаях используется замена
![]() .
.
Пример
2.
![]()
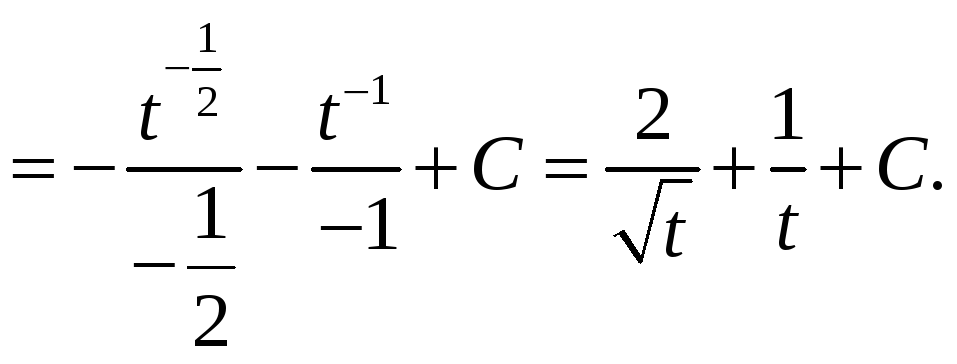
2.
Функция
![]() нечётна относительно cos
x,
если выполняется равенство
нечётна относительно cos
x,
если выполняется равенство
![]() .
В таких случаях используется замена
.
В таких случаях используется замена
![]() .
.
Пример
3.
![]()
![]() .
.
Каждый из этих интегралов можно найти, используя метод неопределённых коэффициентов и метод замены переменной.
3.
Если при смене знака одновременно sin
x
и cos
x
функция не меняет знака, т.е.
![]() ,
то используется замена
,
то используется замена
![]() или
или
![]() .
.
Пример
4.
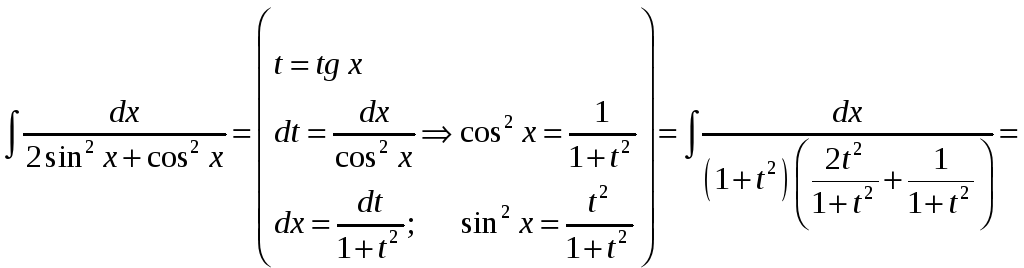
![]() .
.
4.
а)
Интегрирование выражений вида
![]() (
(![]() - действительные числа). Вычисление
таких интегралов основано на разложении
произведения sin
и cos
в виде их разности или суммы:
- действительные числа). Вычисление
таких интегралов основано на разложении
произведения sin
и cos
в виде их разности или суммы:
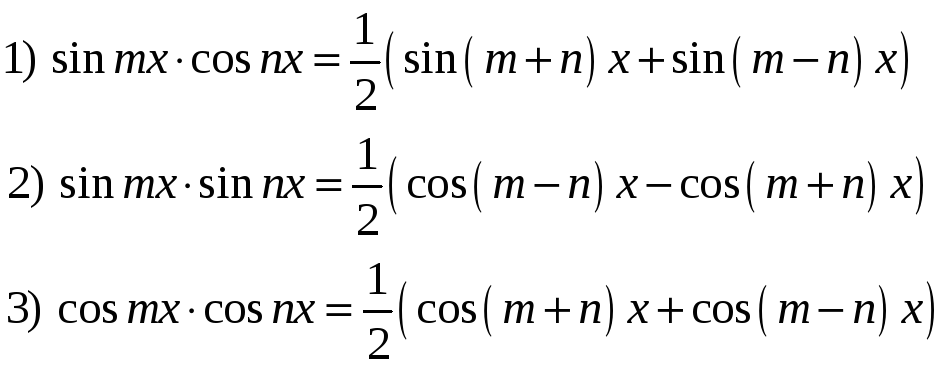
б)
Интегрирование выражений вида![]() .
.
Интегрирование
таких выражений осуществляется с помощью
замены:
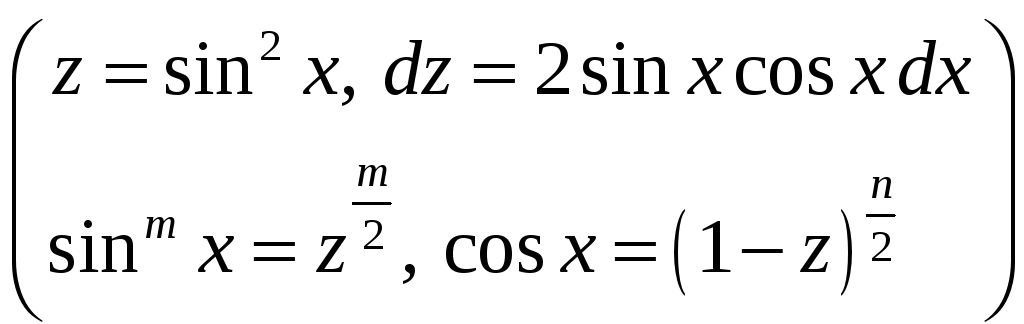 .
Подставляя новую переменную в интеграл,
получим:
.
Подставляя новую переменную в интеграл,
получим:
![]() .
.
Задания для самостоятельного решения
Найти интегралы:
1.
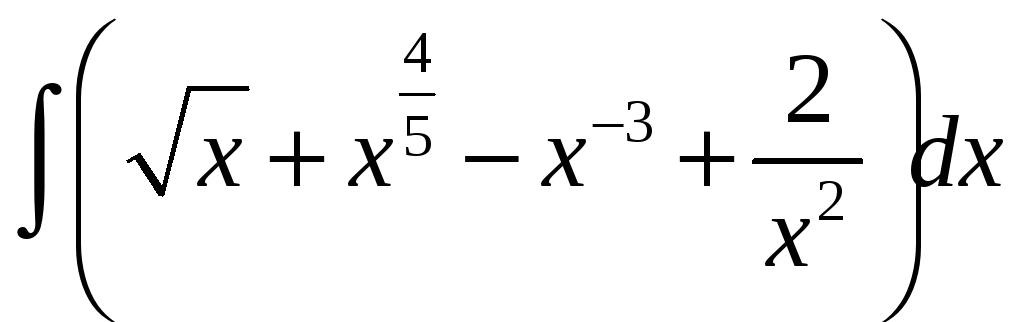 2.
2.
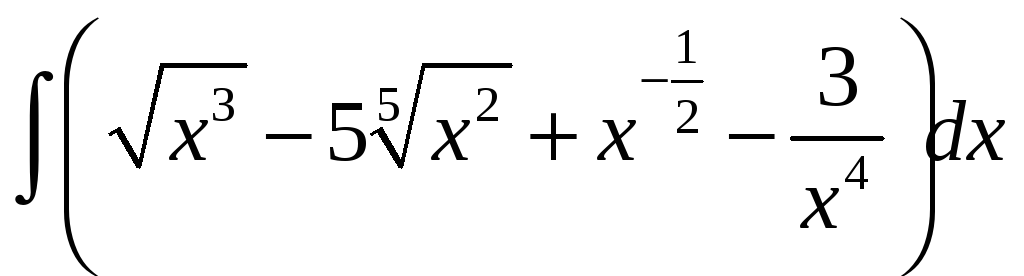 3.
3.
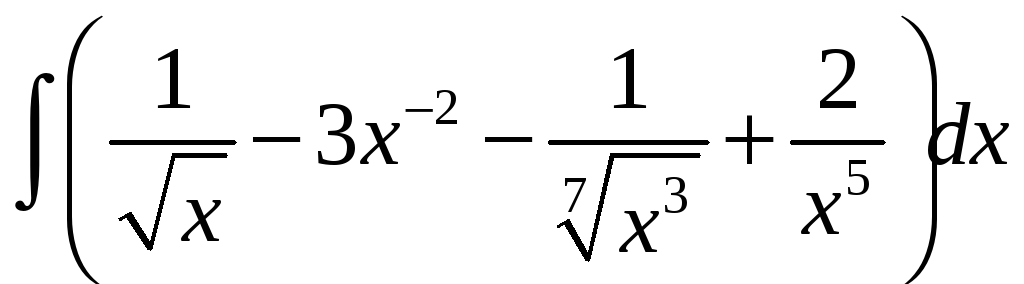
4.
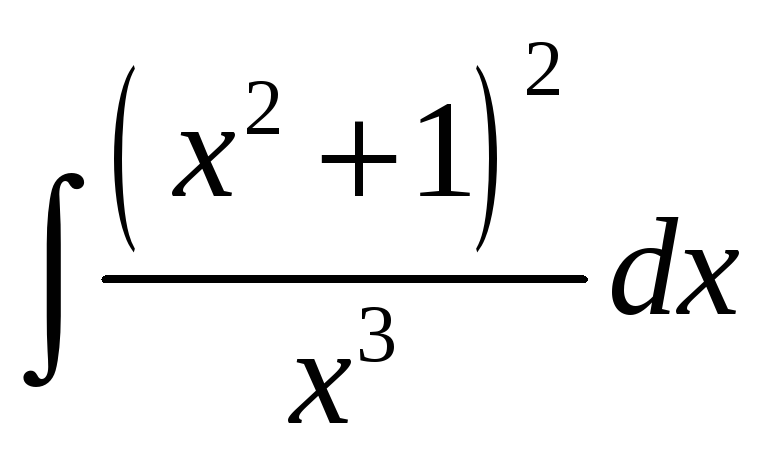 5.
5.
![]() 6.
6.
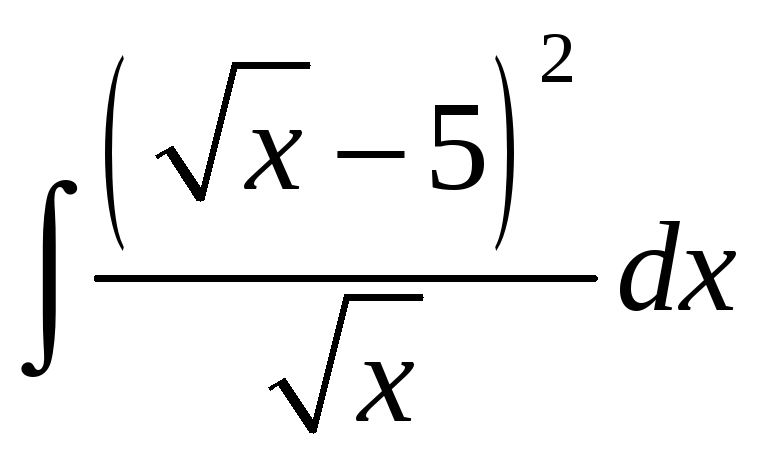 7.
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]() 11.
11.
![]() 12.
12.
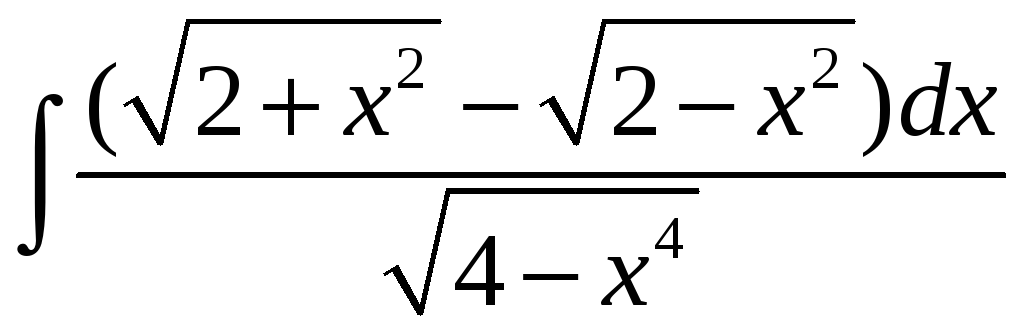
13.
![]() 14.
14.
![]() 15.
15.
![]() 16.
16.
![]()
Найти интегралы, используя метод замены переменной или подведение под знак дифференциала:
17.
![]() 18.
18.
![]() 19.
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]() 23.
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]() 27.
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]() 31.
31.
![]() 32.
32.
![]()
33.
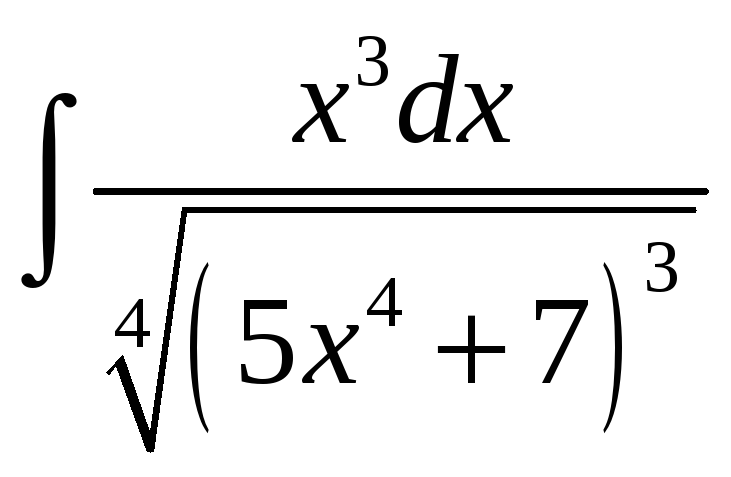 34.
34.
![]() 35.
35.
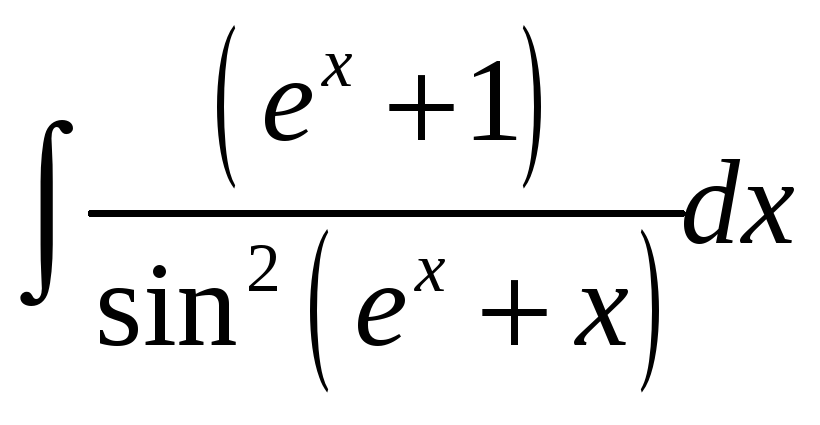 36.
36.
![]()
37.
![]() 38.
38.
![]() 39.
39.
![]() 40.
40.
![]()
Найти интегралы, используя метод интегрирования по частям:
41.
![]() 42.
42.
![]() 43.
43.
![]()
44.
![]() 45.
45.
![]() 46.
46.
![]()
47.
![]() 48.
48.
![]() 49.
49.
![]() 50.
50.
![]()
51.
![]() 52.
52.
![]() 53.
53.
![]() 54.
54.
![]()
Найти интегралы рациональных функций:
55.
![]() 56.
56.
![]() 57.
57.
![]()
58.
![]() 59.
59.
![]() 60.
60.
![]()
61.
 62.
62.
![]() 63.
63.
![]()
64.
![]() 65.
65.
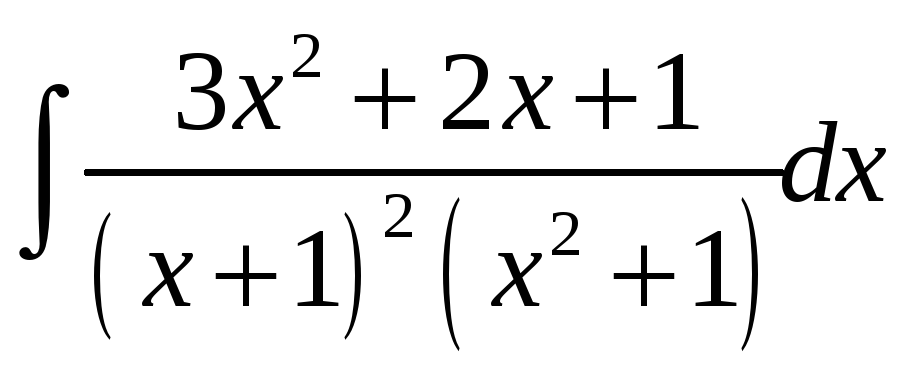 66.
66.
![]()
67.
![]() 68.
68.
![]() 69.
69.
![]()
Найти интегралы иррациональных функций:
70.
![]() 71.
71.
![]() 72.
72.
![]() 73.
73.
![]()
74.
![]() 75.
75.
![]() 76.
76.
![]() 77.
77.
![]()
78.
![]() 79.
79.
![]() 80.
80.
![]() 81.
81.
![]()
82.
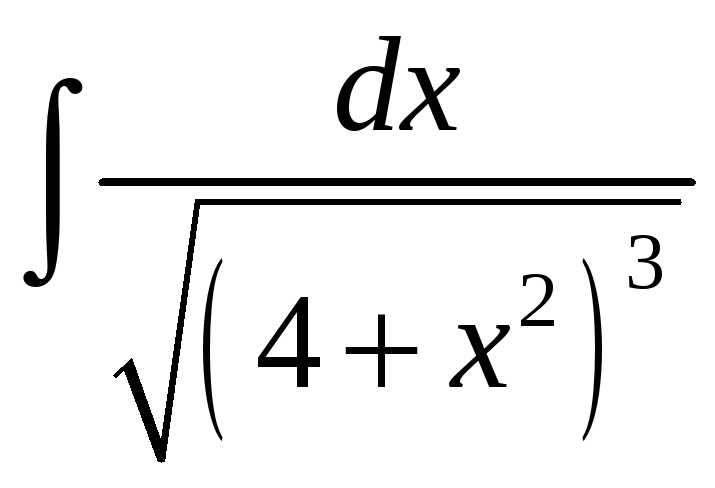 83.
83.
![]() 84.
84.
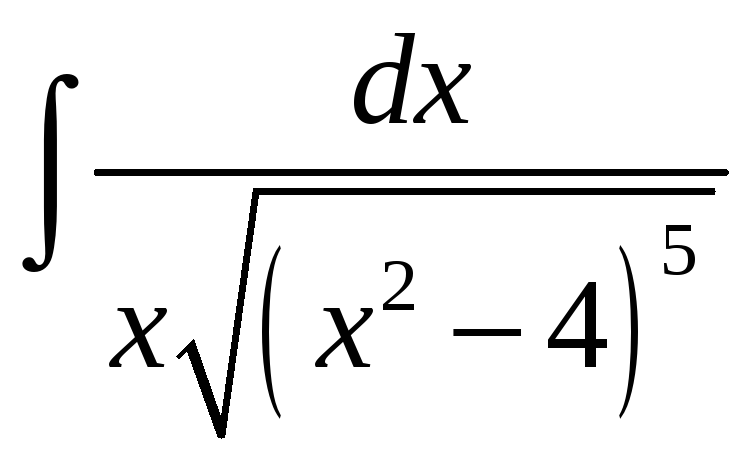 85.
85.
![]()
86.
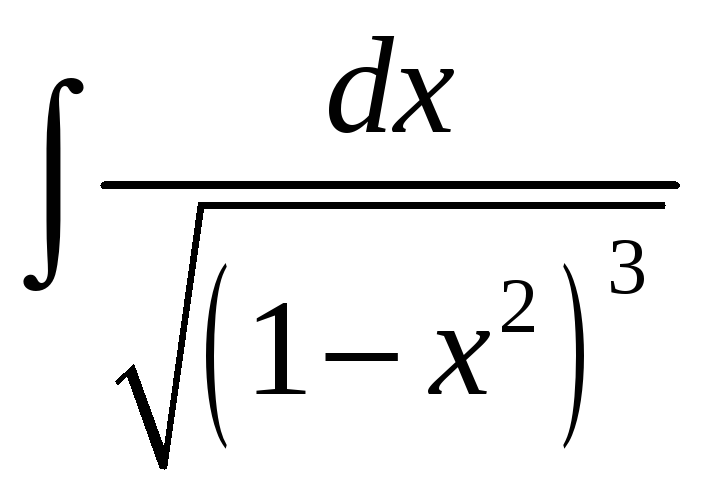 87.
87.
![]() 88.
88.
![]() 89.
89.
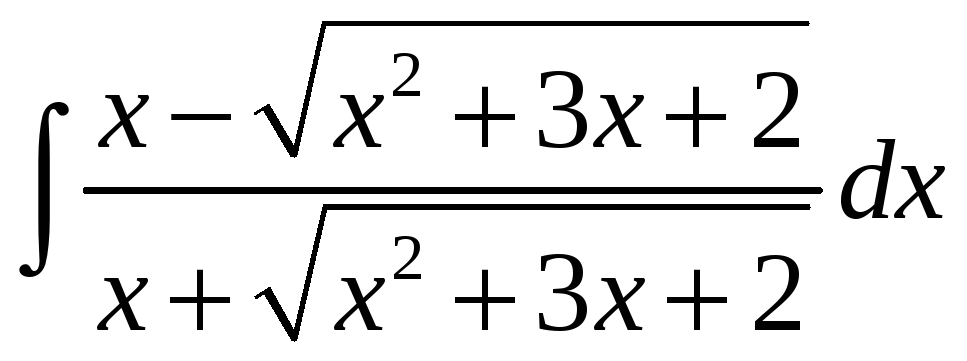
Найти интегралы тригонометрических функций:
90.
![]() 91.
91.
![]() 92.
92.
![]() 93.
93.
![]()
94.
![]() 95.
95.
![]() 96.
96.
![]()
97.
![]() 98.
98.
![]() 99.
99.
![]() 100.
100.
![]()
101.
![]() 102.
102.
![]() 103.
103.
![]()
