Метод замены переменной. Подведение под знак дифференциала

При нахождении многих интегралов оказывается эффективным следующее: вместо исходной переменной х вводится переменная (где

φ – дифференцируемая функция) таким образом, чтобы относительно новой переменной интеграл был значительно проще. Вычисляется преобразованный интеграл, затем осуществляется возвращение к прежней переменной.

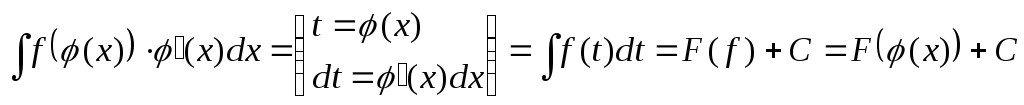
Примеры. Найти интегралы:

1.

Решение.

Обозначим sin x через переменную t, найдём дифференциал. Нахождение дифференциала сводится к нахождению производной и умножению полученной производной на dx:.

Подставим найденные значения в исходный интеграл, в новом интеграле теперь должны присутствовать только функции, содержащие переменную t. Полученный интеграл является табличным, находим его значение и возвращаемся к прежней переменной х.

.

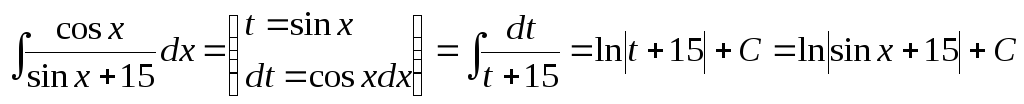2.

Решение. Обозначим знаменатель за новую переменную, найдём дифференциал: . Подставим эти значения в исходный интеграл и найдём его значение:

.

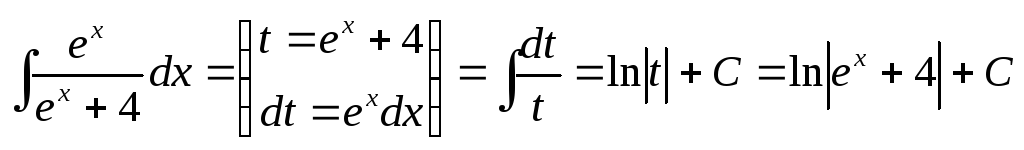3. .

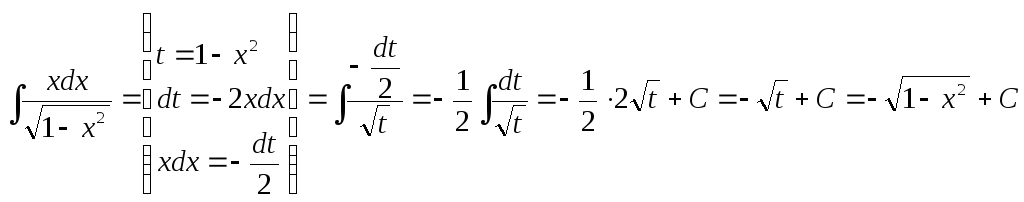4. .

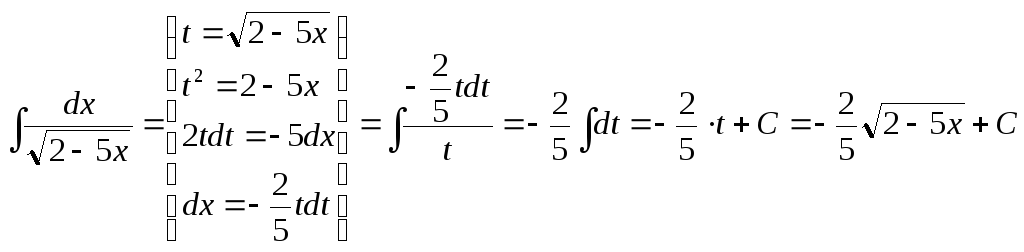Так как часто встречаются интегралы вида или сводящиеся к такому виду, то выбор функции для замены на новую переменную основан на том, что дифференциал от этой функции должен быть равен выражению, находящемуся в исходном интеграле.

В некоторых случаях удобнее использовать метод подведения под знак дифференциала: .

1. Подведение под знак дифференциала постоянного слагаемого:

если , то , а = const.

Пример: .

2. Подведение под знак дифференциала постоянного множителя:

если , то , а = const.

Примеры: а) .

б) .

Пример:

Решение. Представим подынтегральную функцию в виде суммы двух дробей и запишем интеграл в виде суммы двух интегралов. Для каждого из полученных интегралов применим метод внесения под знак дифференциала.

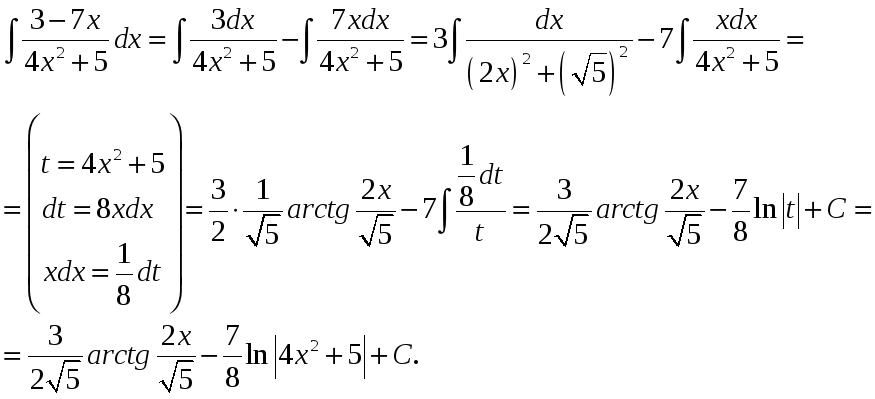
Метод интегрирования по частям

Пусть u = u(x), v = v(x) – дифференцируемые функции.

Формула интегрирования по частям: .

Для применения этой формулы подынтегральное выражение разбивается на две части, одну из которых принимают за u, а другую за dv так, чтобы легко находился интеграл от dv и интеграл  вычислялся проще, чем исходный.

Рассмотрим различные типы интегралов и соответствующие рекомендации по выбору u и dv, для которых формула интегрирования по частям всегда является эффективной, т.е. приводит к более простому интегралу по сравнению с первоначальным. Отметим, что применение формулы интегрирования по частям не ограничивается только этими случаями.

Правила выбора u

1. Если подынтегральная функция содержит в качестве множителя функцию: , , arcsin х, arccos x, arctg x, arcctg x, то в качестве u выбирается это выражение.

2. Если подынтегральная функция имеет вид: , , , где Р(х) – многочлен, то в качестве u выбирается Р(х).

3. Если подынтегральная функция имеет вид: , , , , тогда дважды применяется интегрирование по частям, в качестве u выбирается любая из этих функций.

Пример 1.

Решение. В качестве u выбирается х, т.к. подынтегральная функция имеет вид , Р(х) в данном случае равен х. Оставшееся выражение обозначается dv: . Далее, находим du, то есть дифференциал функции u (который равен производной, умноженной на dx). Затем находим и применяем формулу интегрирования по частям.

.

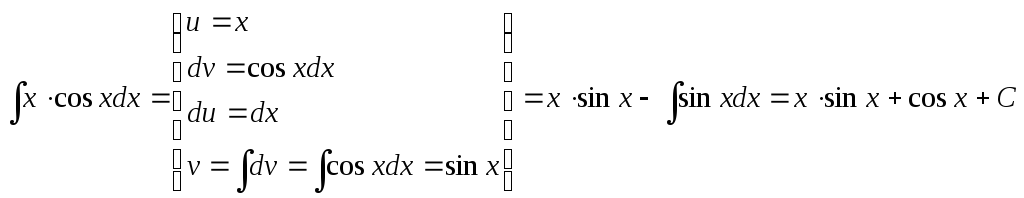Заметим, что формула интегрирования по частям может применяться несколько раз, до тех пор, пока не будет получен интеграл, найти который можно по таблице или другим методом.

Пример 2.

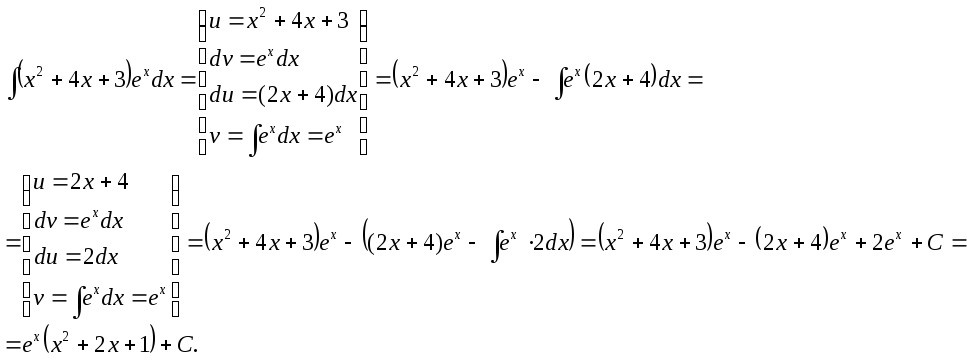
В данном примере два раза применялась формула интегрирования по частям. После первого применения интеграл несколько упростился (степень многочлена уменьшилась на 1), но не был приведён к табличному. После второго применения формулы интеграл был сведён к табличному.

Пример 3.

.

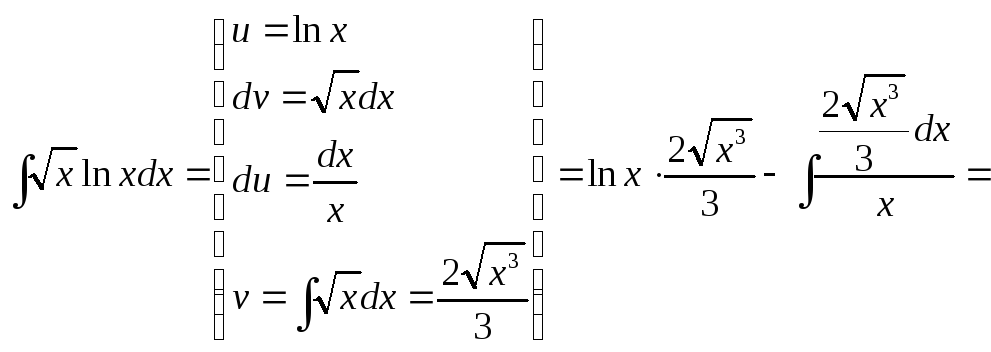
Пример 4.

Решение.

Данный интеграл относится к третьему типу (подынтегральная функция имеет вид ), поэтому в качестве u можно выбрать любую их функций или . Пусть , тогда .

Обозначим исходный интеграл и применим формулу интегрирования по частям:.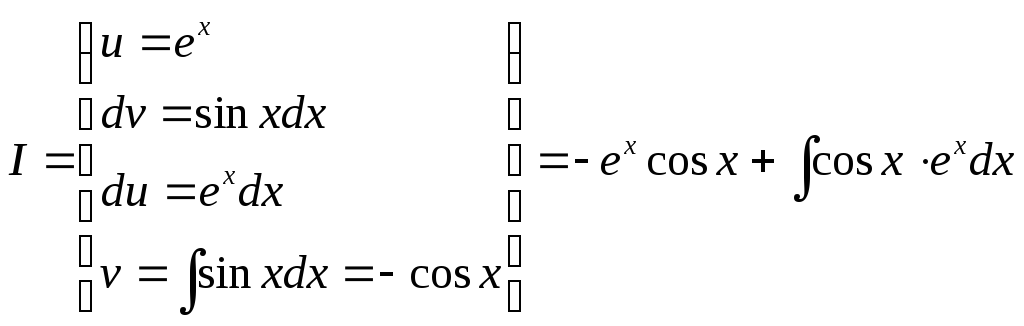

Далее, нужно ещё раз применить формулу, взяв за u ту же функцию, что и в первый раз:

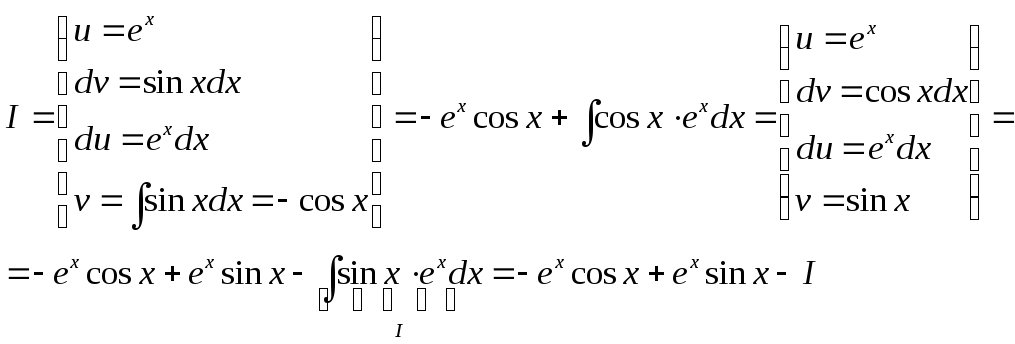
Запишем отдельно в виде уравнения относительно I и решим его:

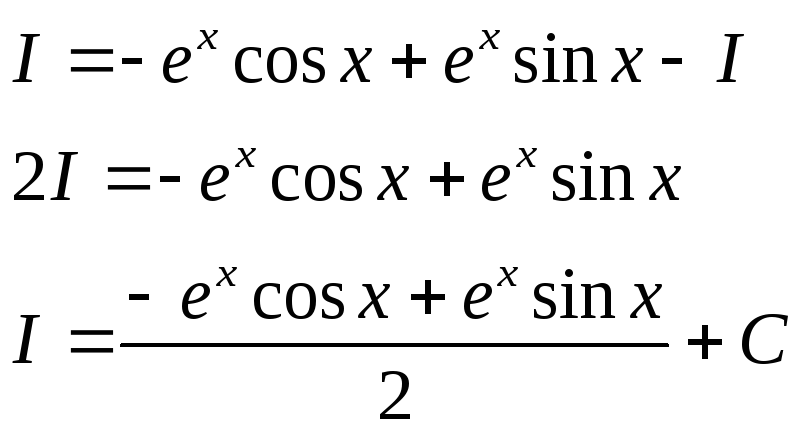
Таким образом, мы нашли значение исходного интеграла I.