5. Применение производной к исследованию функций Возрастание и убывание функций. Локальный экстремум функции
Функция
y
= f(x)
называется возрастающей
(убывающей)
на некотором интервале, если для любых
двух чисел
и
из этого интервала из неравенства
следует
неравенство
(соответственно
Если
функция f(x)
дифференцируема на некотором интервале
и для всех х
из него
то f(x)
возрастает на этом интервале, если же
то убывает.
Часто
область определения функции можно
разбить на конечное число интервалов
монотонности,
каждый из которых ограничен критическими
точками, в
которых
или не существует.
Если
существует такая окрестность
точки
что для всех точек
из нее выполняется неравенство
(или
то точка
называется точкой
минимума (максимума)
функции y
= f(x),
а число
минимумом
(максимумом)
функции.
Точки минимума и максимума функции называются ее точками экстремума.
Необходимое условие экстремума функции.
Если
функция y
= f(x)
имеет экстремум в точке
то
или
не существует, то есть
критическая точка функции f(x).
Обратное, вообще говоря, не верно. Экстремум в таких точках может быть, а может и не быть.
Достаточные условия экстремума функции.
1)
Пусть функция
f(x)
дифференцируема в некоторой окрестности
критической точки
за исключением, быть может, самой этой
точки. Если при переходе через точку
слева направо производная
меняет знак
с плюса на минус (с минуса на плюс), то
функция f(x) имеет максимум в точке
(минимум). Если же
не меняет знака при
то точка
не является точкой экстремума.
2)
Пусть функция
f(x)
дважды дифференцируема в критической
точке
и в некоторой ее окрестности. Если
то
-
точка максимума функции f(x),
а если
то
-
точка минимума функции.
Пример
1. Исследовать
на монотонность
и найти экстремумы функции
Решение.
Область определения функции – вся
числовая ось. Производная
Приравниваем производную к нулю и
решаем уравнение:
-
критические точки. Определим знаки
производной методом интервалов.
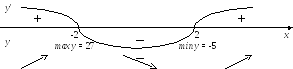
Для
производная
следовательно, функция возрастает, а
для
следовательно, функция убывает на
интервале (-2; 2).
Так как при переходе через точку x = - 2 производная функции меняет знак с плюса на минус, то в точке x = - 2 функция имеет максимум
В
точке х
= 2 функция имеет минимум
Пример
2. Исследовать
на монотонность и найти экстремумы
функции
Решение.
1.
Область определения функции
2. Производная функции
3.
Находим критические точки. Производная
не существует в точке
где и функция также не определена.
Находим нули производной:
4x(x
– 1) = 0,
4.
Исследуем знаки производной на интервалах
с границами в критических точках. (Так
как знаменатель дроби
то он на знак производной не влияет).
Определяем знак числителя методом
интервалов.
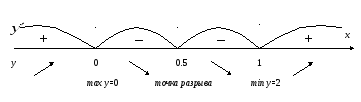
Функция
возрастает при
убывает при
x = 0 - точка максимума функции, max y = y(0) = 0, x = 1 – точка минимума функции, min y = y(1) = 2.