
- •Комплексные числа
- •Операции над комплексными числами
- •2. Числовые последовательности
- •3. Понятие функции. Предел и непрерывность функции
- •Методы раскрытия неопределённостей при вычислении пределов функций
- •Эквивалентные бесконечно малые величины
- •Непрерывность функции. Классификация точек разрыва
- •Классификация точек разрыва
- •4. Производная и дифференциал функции
- •Правила дифференцирования
- •Дифференциал функции
- •Производные высших порядков
- •Применение производной в экономике. Эластичность функции
- •5. Применение производной к исследованию функций Возрастание и убывание функций. Локальный экстремум функции
- •Наибольшее и наименьшее значения функции
- •Правила Лопиталя для раскрытия неопределенностей
- •Выпуклость, вогнутость и точки перегиба графика функции
- •Асимптоты графика функции
- •Исследование функций и построение графиков
- •Примерные варианты контрольной работы № 1 по математическому анализу
- •6. Неопределённый интеграл Первообразная. Неопределённый интеграл
- •Основные методы интегрирования Метод разложения
- •Метод замены переменной. Подведение под знак дифференциала
- •Метод интегрирования по частям
- •Интегрирование дробно-рациональных выражений
- •Метод неопределённых коэффициентов
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
Применение производной в экономике. Эластичность функции
Для исследования экономических процессов часто применяется понятие эластичности функции.
Эластичностью называют предел отношения относительного приращения функции y к относительному приращению аргумента
![]()
![]() (темп
изменения функции)
(темп
изменения функции)![]() эластичность
показывает приближенно на сколько
процентов измениться функция при
изменении аргумента на 1%.
эластичность
показывает приближенно на сколько
процентов измениться функция при
изменении аргумента на 1%.
Свойства эластичности
1.
![]()
2. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций:
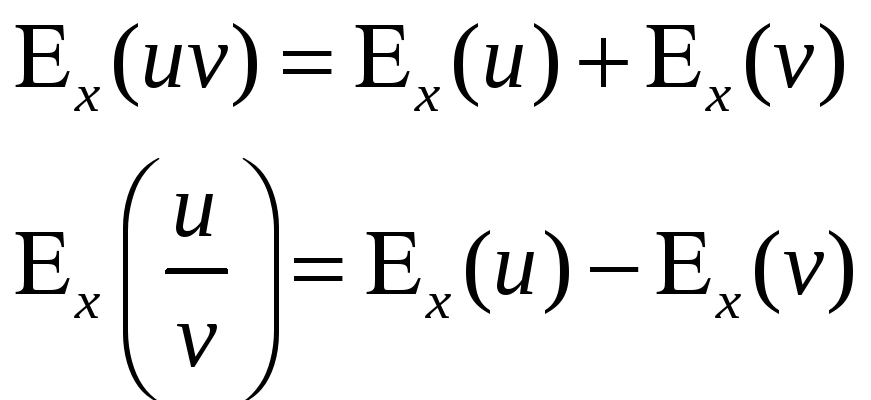
3. Эластичности взаимообратных функций – взаимообратные величины:
![]()
Эластичность применяется при анализе спроса и предложения. Если эластичность по абсолютной величине больше 1, то спрос эластичен, если меньше 1, то спрос не эластичен:
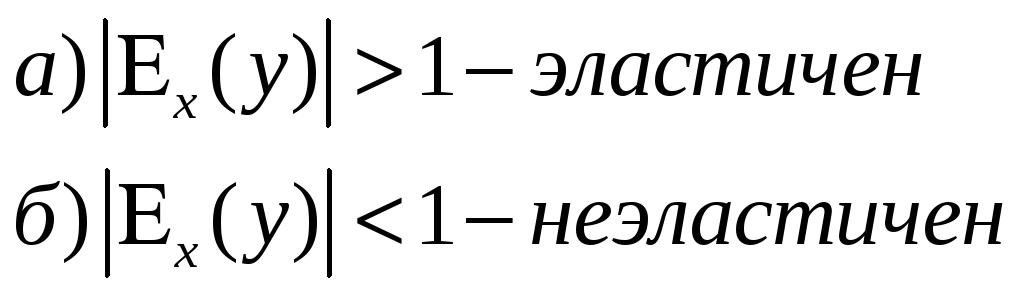
Если спрос неэластичен (![]() ),
то предельный доход отрицателен при
любой цене. Если спрос эластичен, то
предельный доход положителен.
),
то предельный доход отрицателен при
любой цене. Если спрос эластичен, то
предельный доход положителен.
С возрастанием цены для продукции эластичного спроса суммарный доход от реализации продукции увеличивается, а для товаров неэластичного спроса – уменьшается.
Примеры.
1. Зависимость между себестоимостью
единицы продукции y
(тыс. руб.) и выпуском продукции х
(млрд. руб.) выражается функцией
![]() .
Найти эластичность себестоимости при
выпуске продукции, равном 60 млн. руб.
.
Найти эластичность себестоимости при
выпуске продукции, равном 60 млн. руб.
Решение.
Находим
эластичность себестоимости
![]() .
.
При
![]() ,
т.е. при выпуске продукции, равном 60 млн.
руб., увеличение его на 1% приведет к
снижению себестоимости на 0,6%.
,
т.е. при выпуске продукции, равном 60 млн.
руб., увеличение его на 1% приведет к
снижению себестоимости на 0,6%.
2.
Зависимость между издержками производства
y и объёмом выпускаемой
продукции х выражается функцией
![]() (ден.ед). Определить средние и предельные
издержки при объёме продукции 10 ед.
(ден.ед). Определить средние и предельные
издержки при объёме продукции 10 ед.
Решение.
Функция
средних издержек (на единицу продукции)
выражается отношением
![]() ;
при
;
при
![]() средние издержки (на единицу продукции)
равны
средние издержки (на единицу продукции)
равны
![]() (ден.ед.).
(ден.ед.).
Функция
предельных издержек выражается
производной
![]() при
при
![]() предельные издержки составят
предельные издержки составят
![]() (ден.ед.).
(ден.ед.).
3.
Даны функции спроса и предложения
![]() и
и
![]() ,
где q и s
– количество товара, соответственно
покупаемого и предлагаемого на продажу
в единицу времени, р – цена товара.
Найти равновесную цену и эластичность
спроса и предложения для этой цены.
,
где q и s
– количество товара, соответственно
покупаемого и предлагаемого на продажу
в единицу времени, р – цена товара.
Найти равновесную цену и эластичность
спроса и предложения для этой цены.
Решение.
Равновесная цена – цена, при которой спрос и предложение уравновешиваются, она определяется из условия q = s:
![]() ,
т.е. равновесная цена равна 2 ден. ед.
,
т.е. равновесная цена равна 2 ден. ед.
Эластичности по спросу и предложению:
![]() .
.
Для равновесной цены p = 2 находим:
![]() .
.
Так как полученные значения эластичностей по абсолютной величине меньше 1, то и спрос и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это означает, что изменение цены не приведёт к резкому изменению спроса и предложения. Так, при увеличении цены р на 1% спрос уменьшится на 0,3%, а предложение увеличится на 0,8%.
Задания для самостоятельного решения
Найти производные функций:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
y = xctg4x
4.
y = xctg4x
5.
![]() 6.
6.
![]() 7.
7.
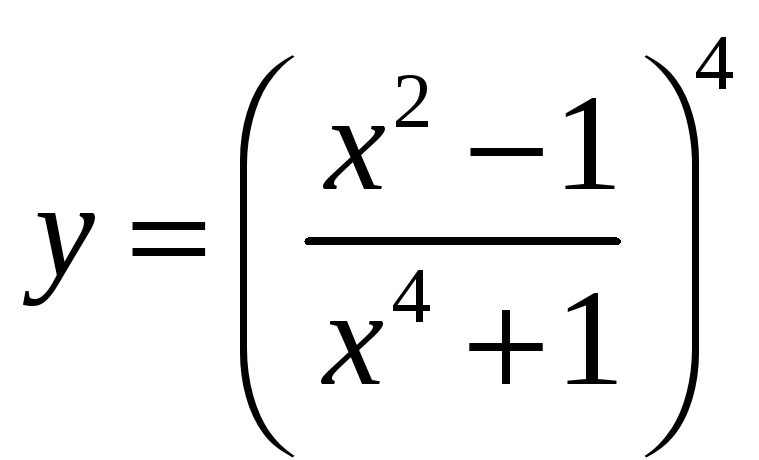 8.
8.
![]()
9.
![]() 10.
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.![]() 15.
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]() 19.
19.
![]() Найти
производные функций и вычислить их
значения при
Найти
производные функций и вычислить их
значения при
![]() :
:
20.
![]()
21
![]()
22.
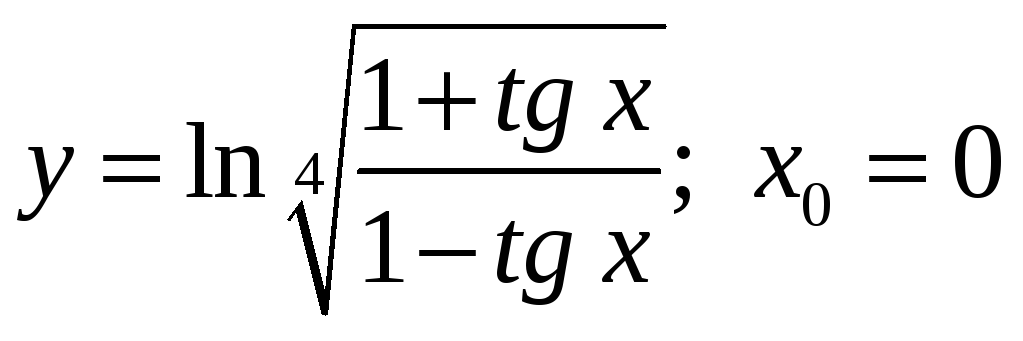 .
.
Найти производные первого и второго порядка для функций:
23.
![]()
24.
![]()
25.
![]()
26.
Зависимость между издержками производства
y
(ден.ед.) и объёмом выпускаемой продукции
х
(ед.) выражается функцией
![]() .
Определить средние и предельные издержки
при объёме продукции, равном 5 ед.
.
Определить средние и предельные издержки
при объёме продукции, равном 5 ед.
27.
Даны функции спроса и предложения
![]() и
и
![]() .
Найти равновесную цену и эластичность
спроса и предложения для этой цены.
.
Найти равновесную цену и эластичность
спроса и предложения для этой цены.
