4. Производная и дифференциал функции

Производной функции y = f(x) в точке называется предел отношения приращения функции в этой точке к приращению аргумента при

Операция нахождения производной называется дифференцированием.

Производная – это скорость изменения функции. Из определения производной следует ее геометрический смысл: производная равна угловому коэффициенту касательной к графику функции в точке : где - угол наклона касательной.

Уравнение касательной к кривой y = f(x) в точке имеет вид

Производные функций находят, используя таблицу производных и правила дифференцирования.

Таблица производных

Функция y	Производная y′	Функция y	Производная y′
	с (с – число)
x	1	tg х
		ctg х
		arcsin х
		arccos х
ex	ex	arctg х
ln x		arcctg х

Правила дифференцирования

1.

2.

3.

4. Если функция дифференцируема в точке а функция y = f(u) дифференцируема в точке то сложная функция имеет производную в точке равную

Примеры. Найти производные функций:

1.

2.

3.

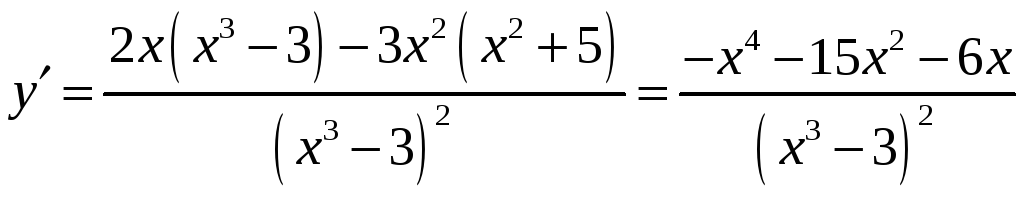
4. . Применим правило дифференцирования сложной функции:

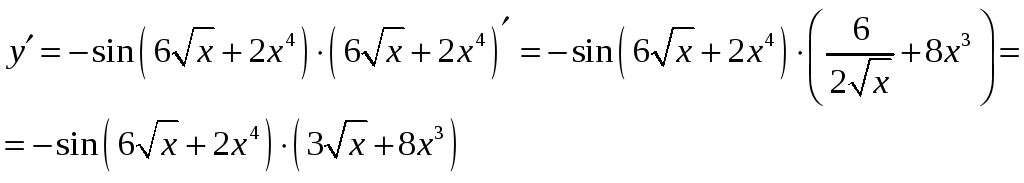
5.

6. . Запишем функцию в виде: .

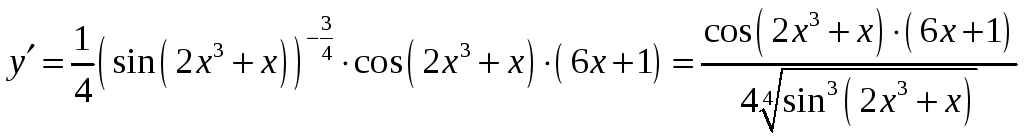
7. Найти производную функции и вычислить её значение при .

; при :.

Дифференциал функции

Если функция y = f(x) имеет конечную производную в точке х, то ее приращение можно записать в виде

где при

Главная, линейная относительно , часть приращения функции называется дифференциалом функции и обозначается dy.

Если y = x, то поэтому дифференциал записывают в виде

при (эквивалентные бесконечно малые), что позволяет использовать при приближенных вычислениях приближенное равенство при малых

Так как то

Пример. Вычислить приближенно arctg 0,98.

Решение.

arctg 0,98 есть частное значение функции f(x) = arctg x при х = 0,98.

Представим arctg 0,98 = arctg (1 – 0,02). Тогда при х = 1,

, учитывая, что , получаем

Производные высших порядков

Производная от функции называется производной первого порядка. Но сама является функцией, которая также может иметь производную. Производной n-го порядка называется производная от производной (n-1)-го порядка.

Обозначаются: - производная второго порядка (или вторая производная), - третьего порядка (или третья производная). Производные более высоких порядков обозначаются арабскими цифрами в скобках либо римскими цифрами, например или .

Пример. Найти производную третьего порядка для функции .

Решение. ; ; .