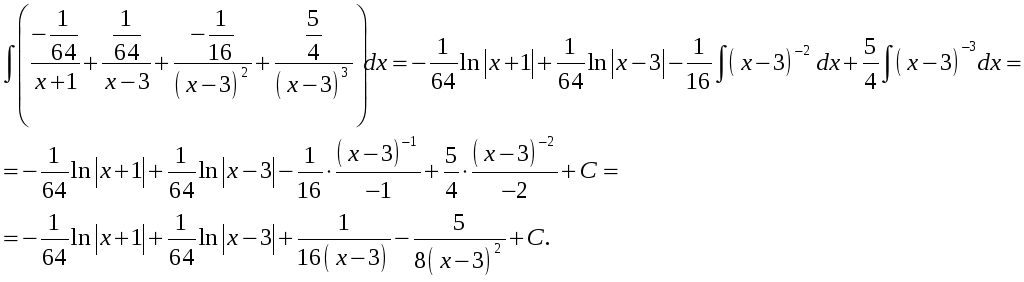Интегрирование дробно-рациональных выражений

Выражение вида называется дробно-рациональной функцией или рациональной дробью, - многочлен степени m, - многочлен степени n. Рациональная дробь называется правильной, если m < n, неправильной – если . Если под интегралом находится неправильная рациональная дробь, то нужно выделить целую часть и найти остаток от деления.

Например, если требуется найти интеграл от дроби , которая является неправильной (степень многочлена в числителе больше степени многочлена в знаменателе), то нужно осуществить деление «уголком».

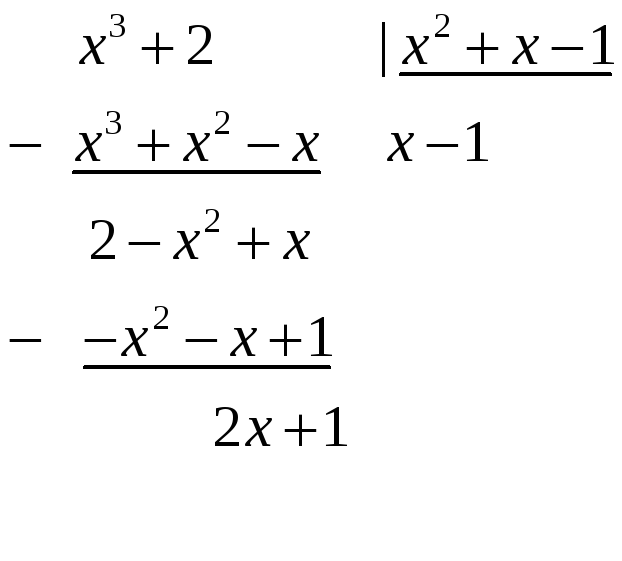
- целая часть, - остаток от деления.

Дробь раскладывается следующим образом: .

В дальнейшем находят интеграл от целой и дробной части. Для нахождения интеграла правильной дроби используется метод неопределённых коэффициентов.

Метод неопределённых коэффициентов

Рассмотрим правильную дробь . Всякий многочлен имеет точно n действительных или комплексно-сопряжённых корней с учётом их кратности, и при этом многочлен может быть представлен в виде сомножителей, содержащих корни этого многочлена.

Например, , где - действительный корень кратности 1, - действительный корень кратности 5, многочлен имеет два комплексно-сопряжённых корня, - содержит 2 комплексно-сопряжённых корня кратности 3.

Всякая правильная рациональная дробь может быть представлена в виде суммы четырёх типов простейших дробей.

1.

2. , k – кратность корня .

3.

4. 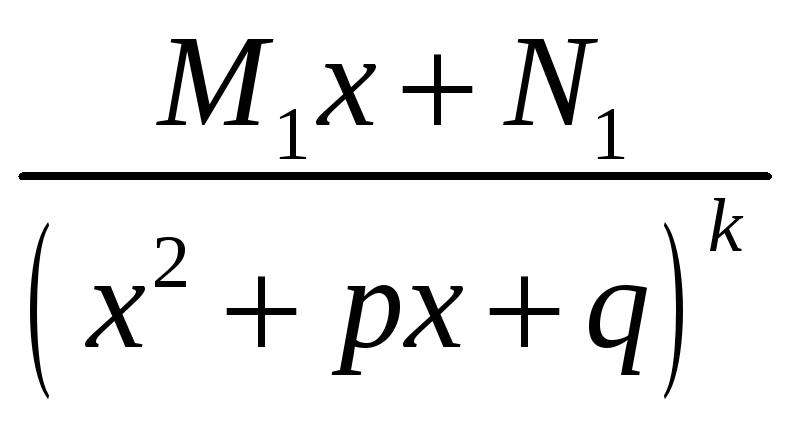- k – кратность пары комплексно-сопряжённых корней.

а) Если в знаменателе корень - корень кратности 1, то ему соответствует одна простейшая дробь 1-го типа.

б) Если корень имеет кратность k, то ему соответствует сумма дробей 1-го и 2-го типа до степени k включительно, т.е. .

Например, для дроби .

в) Если многочлену соответствует пара простых комплексно-сопряжённых корней, то в разложении ему соответствует одна дробь 3-го типа.

г) Если многочлену соответствуют комплексные корни кратности k, то в разложении для ему соответствует сумма дробей 3-го и 4-го типа до степени k включительно, т.е. .

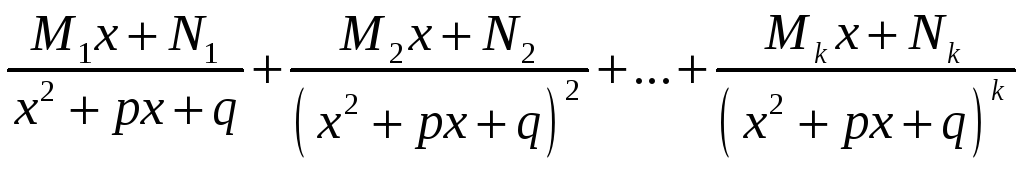Например, для дроби

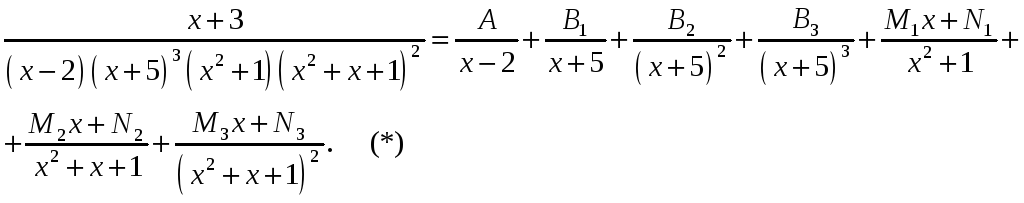
Неизвестные коэффициенты необходимо определить так, чтобы левая и правая части равенства (*) были равны друг другу при любом х. Определение этих коэффициентов проводится методом неопределённых коэффициентов.

Правая часть (*) приводится к общему знаменателю, знаменатели отбрасываются и приравниваются числители левой и правой частей (*).

Далее возможны два пути:

1) В правой части (*) группируются слагаемые с одинаковой степенью х, затем приравниваются коэффициенты при одинаковых степенях х в правой и левой части, из полученной системы линейных алгебраических уравнений находятся неизвестные коэффициенты.

2) В соответствии неизвестных коэффициентов выбираются значения х (лучше брать корни) и подставляются в числители левой и правой части (*); также получается система уравнений для нахождения неизвестных коэффициентов.

Часто используются комбинированно оба способа.

Таким образом, интегрирование рациональных дробей сводится к интегрированию четырёх типов простейших дробей.

Интегрирование дробей 1-го, 2-го и 3-го типов:

1.

2.

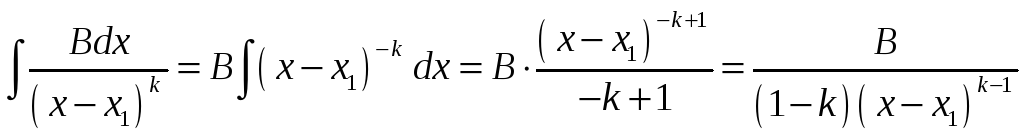
3.

.

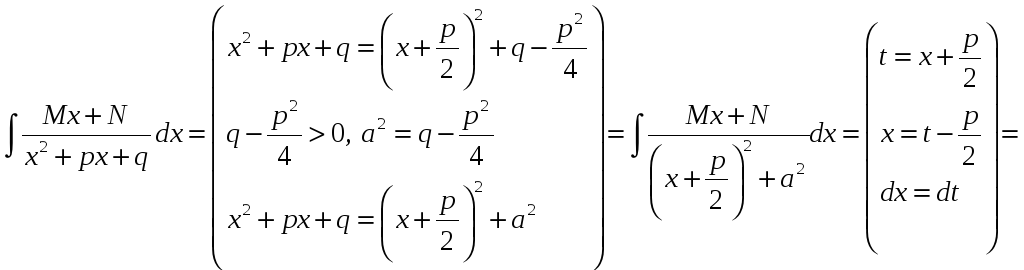
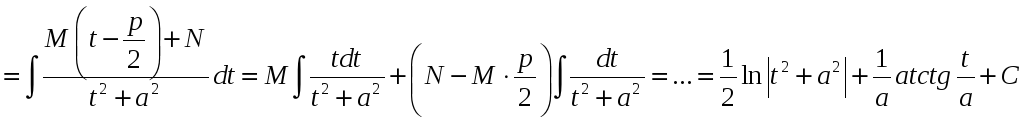Пример 1.

Решение. Запишем рациональную дробь без интеграла: . Она является правильной (степень числителя меньше степени знаменателя). В знаменателе находится квадратный трёхчлен, корни которого равны :

Значит, дробь можно разложить на сумму двух дробей 1-го типа:

.

Приводим дроби к общему знаменателю и записываем только числители:

.

Подставляем по очереди корни знаменателя вместо х и решаем уравнение относительно неопределённых коэффициентов:

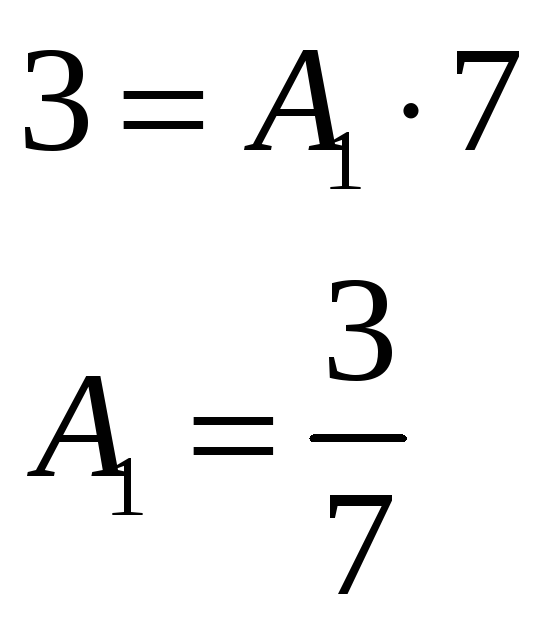
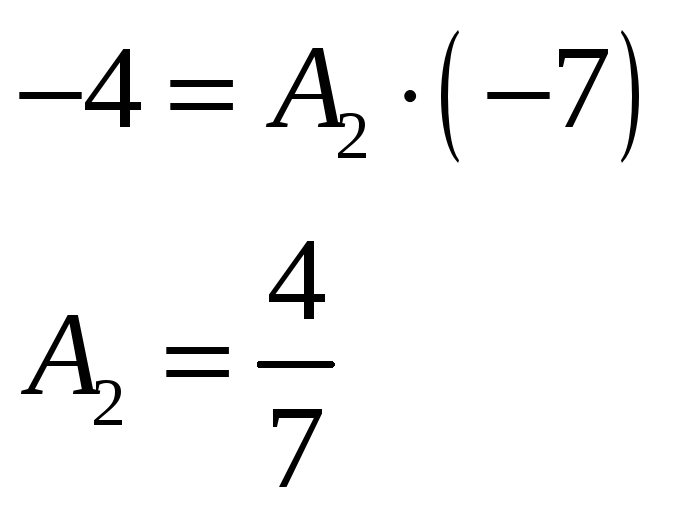
Подставляем найденные коэффициенты в разложение первоначального интеграла и находим интеграл:

.

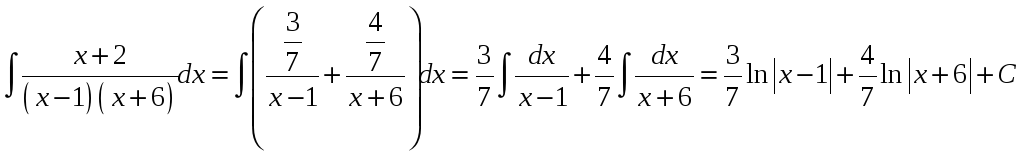Пример 2.

Решение. Дробь правильная. Знаменатель имеет один действительный корень и два комплексных , следовательно, дробь будет раскладываться на сумму дробей 1-го и 3-го типа:

.

(*)

Подставляем корень в полученное равенство (*):

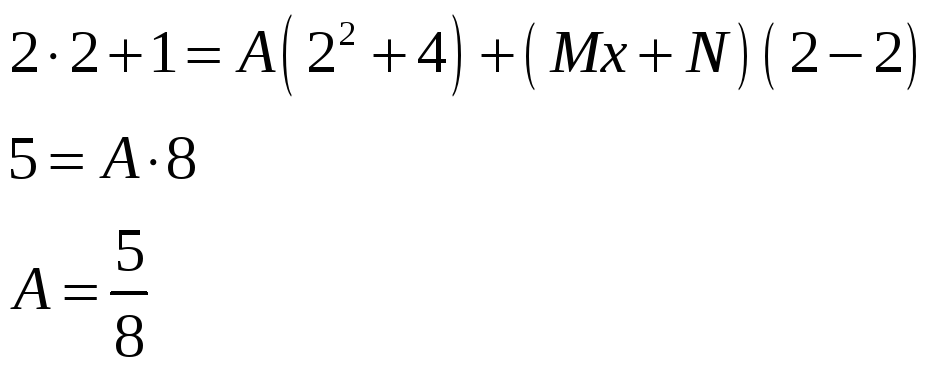
Для того чтобы найти коэффициенты M и N, раскроем скобки в равенстве (*):

.

Вынесем в правой части этого равенства и за скобки:

Таким образом, коэффициенты в правой части равенства сгруппированы по степеням х.

Приравниваем коэффициенты при соответствующих степенях х в левой и правой части равенства:

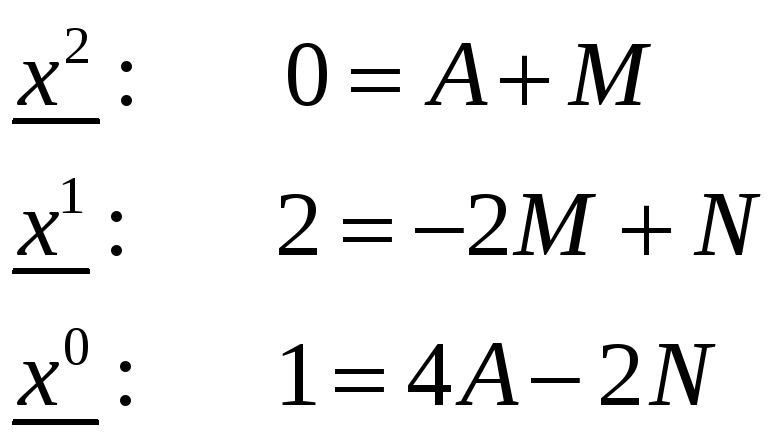
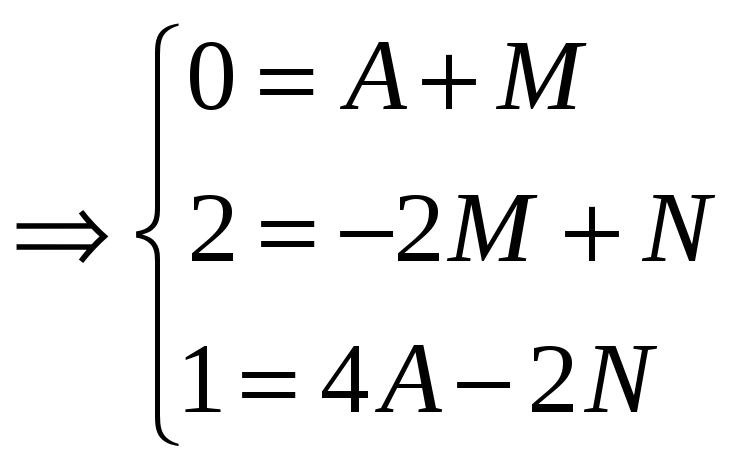
Коэффициент А был найден ранее, подставляем его значение в систему и находим коэффициенты M и N:

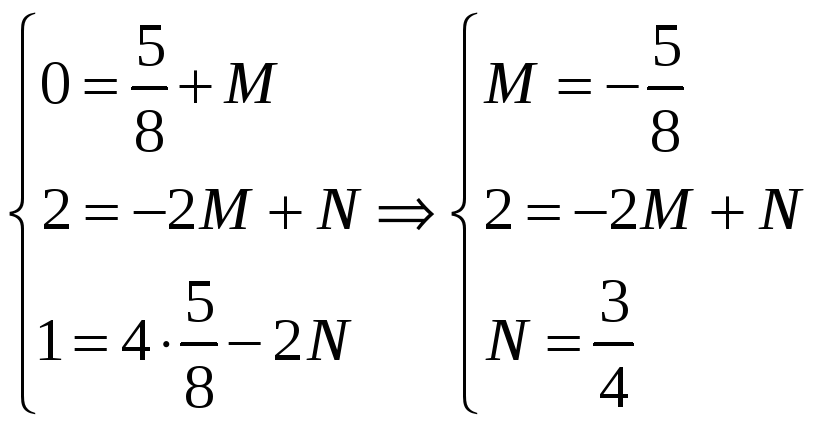
Подставляем найденные коэффициенты A, M, N в разложение первоначального интеграла и находим интеграл:

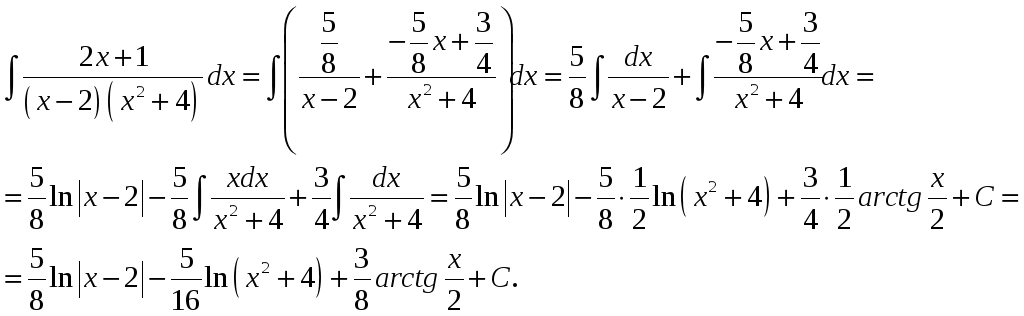
Пример 3.

Решение. Дробь неправильная, т.к. степень числителя (4) больше степени знаменателя (3). Выделим целую часть с помощью деления уголком:

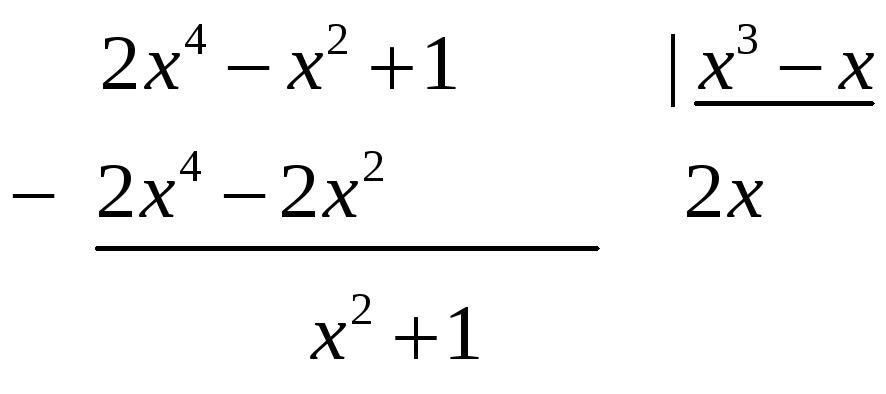
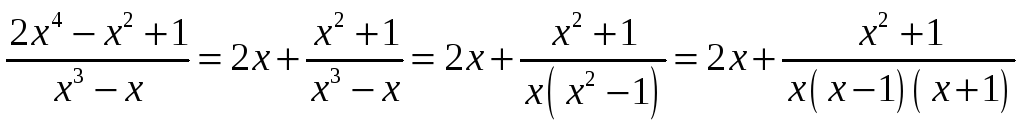
Запишем отдельно правильную дробь и её разложение на 3 дроби 1-го типа:

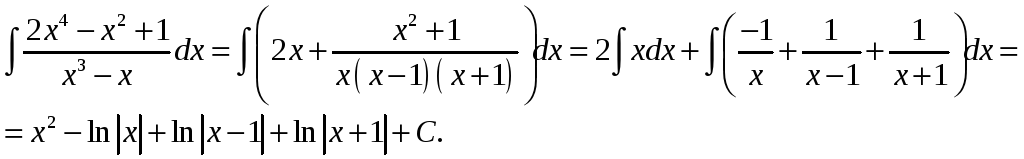
Пример 4.

Решение. Дробь правильная. Знаменатель имеет один действительный корень кратности 1 и 1 действительный корень кратности 3 (т.к. выражение (х – 3) имеет степень 3), следовательно, дробь будет раскладываться на сумму дробей 1-го и 2-го типа:

.

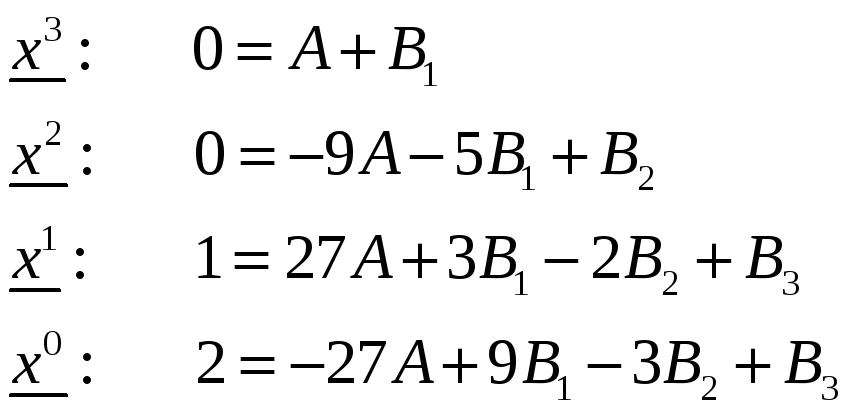
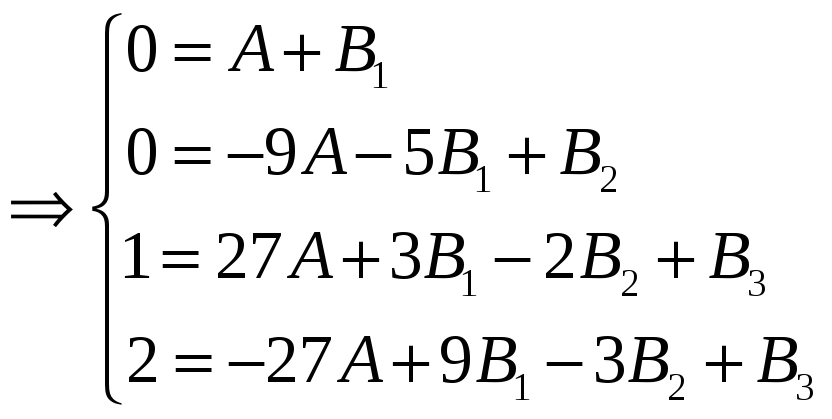
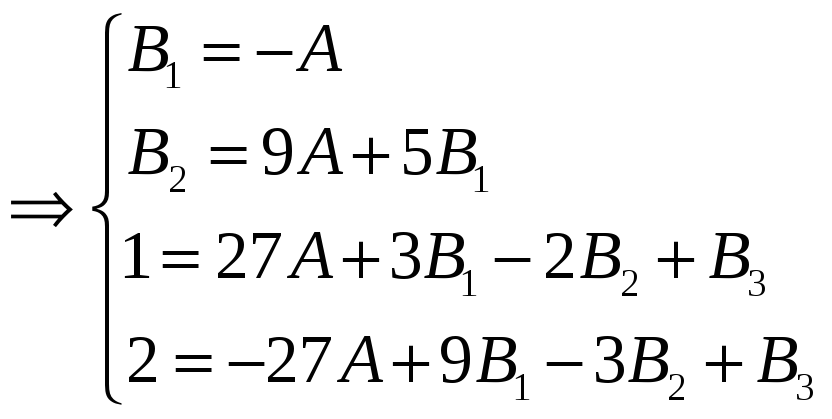
Коэффициенты А и были найдены ранее, подставляем их значения в систему и находим коэффициенты и :.