68.Інтегрув. Раціон. Виразів, до яких входять тригоном. Ф-ії.
Теор.:
за
допом. підстановки
зводиться до інтегр. від раціон. ф-ії
від t.
Довед.:
Одержимо
раціон. ф-ія, що залежить від t.
Прикл.: обчислити інтеграл:
Заув.:
підстановка tgx/2=t
наз.
універсальною, але на практиці у деяких
випадках вона приводить до раціональних
ф-ій з великими степенями t.
Тому
краще користуватися так званими
спеціальними тригонометр. підстановками.
Теор.2:
1.
Якщо підінтегр. ф-ія
непарна
відносно sinx,
тобто
то застосовують підстановку t=cosx;
2. Якщо
підінтегр. ф-ія непарна відносно cosx,
тобто
то застосовують підстановку t=sinx;
3.
Якщо підінтегр. ф-ія парна відносно
своїх аргументів, тобто
то застосов. підстановку tgx=t.
Прикл.:
обчислити інтеграл:
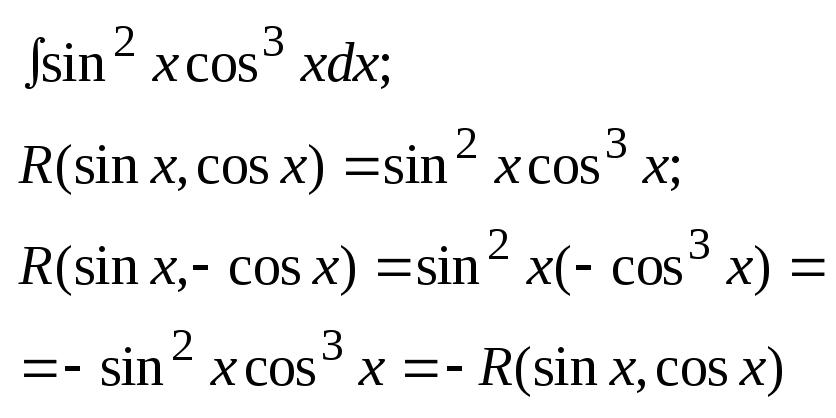Нехай
sinx=t;
69.Означ. Визнач. Інтегралу. Геометр. І фізичний зміст.
Нехай
на [a,b]
визнач.
ф-ія f(x).
Розглян.
довільне розбитя [a,b]
на
n
частин
точками
На кожній із частин
візьмемо довільну т.
і
обчислимо знач. ф-ії f(x)
в
цій точці. Побудуємо суму
де
довжина
.
Позначимо через
найбільш. із довжин відрізків даного
розбитя:
Вираз (1) наз. інтегральн. сумою ф-ії f(x) на [a,b].
Заув.1:
геометр. інтегр. сума(1) = площі ступінчастої
фігури, що утворюється із прямокутників
з основами
і висотами відповідно
.
Заув.2:
зрозуміло, що інтегр. сума (1), взагалі
кажучи, залежить від способу розбитя
[a,b]
на частини і вибору точок
на
кожній із них.
Озн.:
Визначеним інтегр. від ф-ії f(x)
на [a,b]
наз. границя інтегр. суми(1),
,
якщо вона не залежить від способу розбитя
[a,b]
на частини і вибору точок
на кожній із них.
Визнач.
інтегр. познач. символом
В позначені визнач. інтегр. а – нижня межа інтегр.; b – верхня; f(x) – підінтегр. ф-ія; f(x)dx – підінтеграл; х – зміна інтегр.
Геом.
зміст визнач. інтегр.:
для невідємної ф-ії
=
площі криволінійної трапеції, що обмежена
графіком ф-ії y=f(x),
прямими x=a,
x=b
і віссю Ох.
До понятя визначен. інтегр. приводять такі фізичні задачи:
1) шлях,
пройдений матер. точк. з моменту часу а
до b
(t=a,
t=b)
є
визнач. інтеграл від швидкості:
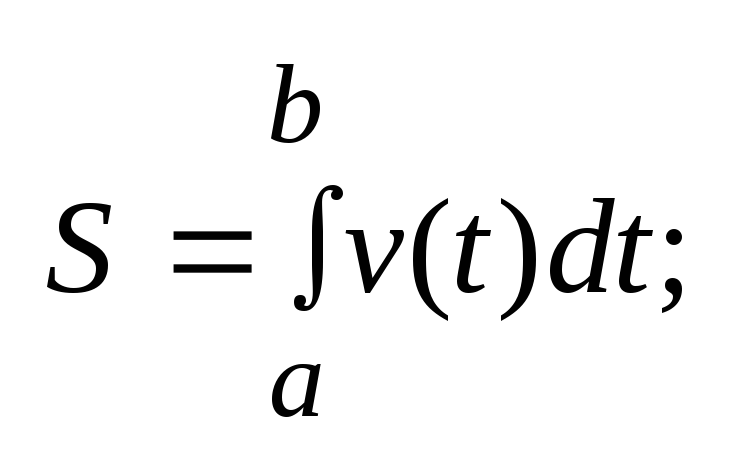
2)
робота
зміної сили F(x)
на
[a,b]:
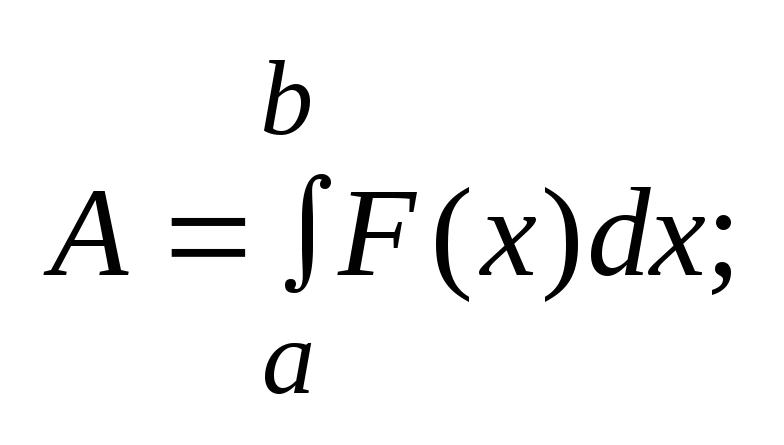
3) маса
неоднорідного стержня = визначеному
інтегр. від його густини:
та інші задачи.
70.Умови існув. Визначен. Інт. Властив. Визнач. Інт., вираж. Рівностями.
Теор.1(необх. умова існув. визн. інт.) Якщо ф-ія f(x) інтегровна на [a,b], то вона обмежена на цьому відрізку.
Заув. твердженя обернене до теор.1 неправільне. З обмеженості ф-ії на відрізку, взагалі, ще не випливає її інтегровності.
Прикладом такої ф-ії є ф-ія Діріхле:
Розгл.
х є [0,1]. Зрозуміло, що D(x)
обмежена, тому що
Побудуємо інтегр. суму
,
взявши спочатку всі точки
раціон.
числами. Одержимо:
З іншого
боку, якщо всі
візьмемо
ірраціон. одержимо:
.
Тобто
значен. інтегр. суми
залежить від способу розбиття відрізка
[0,1]. Це означає, що ф-ія D(x)
неінтегр. на цьому відр.
Теор.2(дост. умова існув. визн. інт.) Якщо ф-ія f(x) непер. на [a,b], то вона інтегр. на цьому відрізку.
Заув. Достат. умова інтегровн. зовсім не означає, що клас інтегровних на [a,b] ф-ій склад. лише з неперервн. ф-ій він значно ширше. Про це свідчать такі твердження:
Теор.3: Якщо ф-ія f(x) обмежена на [a,b] і неперервна на ньому всюди, крім скінченого числа точок, ця ф-ія інтегровна на [a,b].
Теор.4: Якщо ф-ія f(x) інтегровна на [a,b] і якщо змінити її значення у скінченому числі точок, то інтегровність при цьому не порушиться і величина визначеного інтегр. не зміниться.