
- •34.Похідні елемент. Ф-ій
- •35.Похідна складної функції. Похідна функції заданої неявно.
- •36. Похідна оберн. Ф-ії. Диференц. Оберн. Тригоном. Ф-ій.
- •37.Похідна функції, заданної параметрично.
- •38.Гіперболичні функції, їх властивості та похідні.
- •39.Диференціал.Геом. Зміст диференц.
- •40.Властив. Диференц.Інваріантність форми дифер.Застосув. Дифер. У наближ. Значен.
- •Дов. Інваріантність форми дифер.
- •Заст. Дифер. У наближ. Обч.
- •41. Похідні вищих порядків.
- •42. Форм. Лейбніца. Диференц. Вищих порядків.
- •43. Теор. Ферма і Ролля
- •44.Теор. Коші і Лагранжа.
- •45. Правило Лопіталя. Розкриття невизначеності 0/0
- •46.Правило Лопіталя для розкриття невизн.
- •47.Формула Тейлора для многочлена
- •48.Формула Тейлора для ф-ії.
- •49.Форм. Тейлора з залишк. Членом у формі Лагранжа.
- •50.Теор. Про умови сталості ф-ії. Наслідок.
- •51.Ознаки монотоності ф-ії.
- •52.Локальн. Екстремум ф-ії. Теор. Про необхідну умову.
- •53.Перша достатня умова екстр. Ф-ії. Правило дослідж. Ф-ії на екстремум.
- •54.Друга і третя достатні умови локал. Екстр. Ф-ії.
- •55.Опуклість і вгнутість кривих. Теор.1
- •56.Точки перетину кривої. Теореми 2 і 3.
- •57. Асимптоти кривої.
- •1. Вертик. Асимптоти
- •58.Первісна ф-ії і невизн. Інтеграл.
- •Власт. Невизнач. Інтегр.:
- •59.Основні інтегр. Інтегр., що не є елемент. Ф-ми.
- •60. Інтегр. Підстановкою у невизн. Інтегр. Приклади.
- •61.Інтегрув. Частинами у невизн. Інтегралі.
- •62.Обчислення інт.
- •63.Інт., що містять у знамен. Квадр. Трьохчлен. 1,2,3 типи.
- •64.Інтегр., що містять у знам. Кв. Трьохчлен. 4,5,6,7 типи.
- •65.Інтегрув. Дробово-раціон. Ф-ій.
- •66.Інтегрування деяк. Алгебр. Ірраціон. Підст. Ейлера
- •67.Інтегр. Диференц. Біномів. Підстановки Чебишева.
- •68.Інтегрув. Раціон. Виразів, до яких входять тригоном. Ф-ії.
- •69.Означ. Визнач. Інтегралу. Геометр. І фізичний зміст.
- •70.Умови існув. Визначен. Інт. Властив. Визнач. Інт., вираж. Рівностями.
- •Власт. Визн. Інт., вираж. Рівн.
- •71.Власт. Визн. Інт. Виражені нерівн. Теор. Про сер. Знач ф-ії.
- •12) Теор.(про середнє знач. Ф-ії)
- •72.Інтегр. Із змінною верхнюю межою інтегр. Теор. Наслідок.
- •73.Форм. Ньютона-Лейбніца. Заміна змін. У визнач. Інтегр. Інтегр. Частин. У визнач. Інтегр
65.Інтегрув. Дробово-раціон. Ф-ій.
ОЗН.
Ф-ії
 наз.
елементарними дробово-раціон. ф-ми, або
елемент. дробями.
наз.
елементарними дробово-раціон. ф-ми, або
елемент. дробями.
ОЗН.
дробово-раціон. ф-ія
![]() (Pr(x),
Qn(x)
– многочлени степені відповідно r
і n)
наз. правільною, якщо r<n
і неправільною: r
(Pr(x),
Qn(x)
– многочлени степені відповідно r
і n)
наз. правільною, якщо r<n
і неправільною: r![]() n.
n.
Заув.
Якщо раціон. дріб (1) неправільний його
завжди можна подати у вигляді
![]() де r1<n,
M(x)
– деякий
многочлен.
де r1<n,
M(x)
– деякий
многочлен.
Теор.
Якщо знаменник правільною раціон. дробу
![]() можна подати у вигляді
можна подати у вигляді
 то
справедлива формула:
то
справедлива формула:
 Теор.
без доведення. Знаведенної теор. випливає,
що інтегрув. раціон. ф-ії зводиться до
інтегрув. елементарних дробів. У випадку,
коли раціон. ф-ія неправільна:
Теор.
без доведення. Знаведенної теор. випливає,
що інтегрув. раціон. ф-ії зводиться до
інтегрув. елементарних дробів. У випадку,
коли раціон. ф-ія неправільна:

а інтеграл
![]() виражається знову таки через інтегр.
від елемент. дробів. Буквені коеф.
А1,...,Ак1,В1,..., Вкm,E1,…,El1,F1,…,Fl1,M1,…,
виражається знову таки через інтегр.
від елемент. дробів. Буквені коеф.
А1,...,Ак1,В1,..., Вкm,E1,…,El1,F1,…,Fl1,M1,…,
Mls,N1,…,Nls у розкладені раціон. дробу на елемент. дроби невідомі. Для їх знаходження існують 2 методи:
1) метеод прирівняння невизначен. коефіц. при степеня х. Суть його полягає в тому, що після розкладення раціон. ф-ії на елемент. дроби вирази у правій частині приводять до спільного знаменника. В результаті одержимодріб, знамен. якого, співпадає із знамен. вихідної ф-ії, а чисельник містить невідомі буквунні коефю, помножен. на х та його степені. Прирівнюючи цей чисельник і чисельник вихідного дробу одержимо рівняня, з якого будемо приравнювати коеф. при відповідних степен. х. В результаті маємо систему, з якої і визначають невідомі буквені коеф.
2) суть його полягає в тому, що після приведеня елемент. дробів до спільного знамен. і після того, як ми прирівняли чисельники дробів, ми надаємо х конкретних значень стільки скільки є невідомих.
Заув. на практиці зручніше для пошуку невизнач. коеф. застосовувати комбінований метод, при якому частину рівнянь одержують, приравнюючи коеф. при однакових степенях х, а іншу частину рівнянь одержують, надуючи х конкретних значень. Якщо знаменик має дійсні корені, краще надавати саме їх.
66.Інтегрування деяк. Алгебр. Ірраціон. Підст. Ейлера
![]()
1) b2-4ac<0
![]()
знак ax2+bx+c = знак a => a>0
![]() -
-
- 1-а підстановка Ейлера
![]()
![]()

2) b2-4ac>0
![]()
![]() -
-
- 2-га підстановка Ейлера
a(x-x2)=t2(x-x1)

![]()
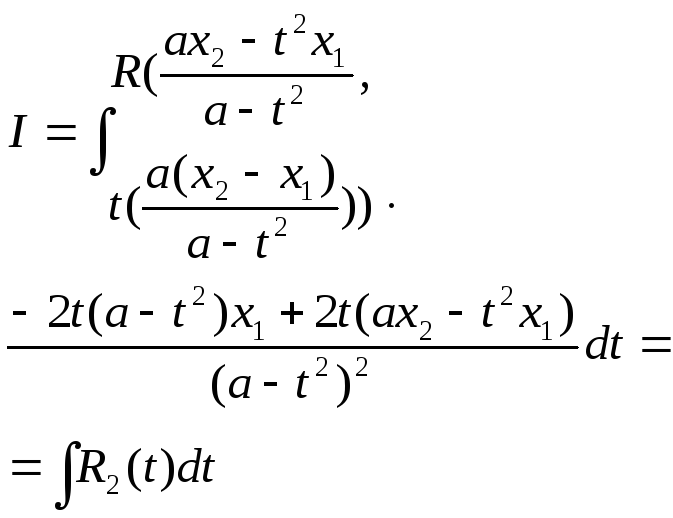
Зауваження 1:
1-у підстановку Ейлера можна застосовувати при b2-4ac>0 при умові а>0
Зауваження 2:
Якщо a<0
але c>0
то можна використовувати 3-тю підстановку
Ейлера
![]() .
Цей випадок можна звести до 1-го якщо
замінити t=1/2
.
Цей випадок можна звести до 1-го якщо
замінити t=1/2
67.Інтегр. Диференц. Біномів. Підстановки Чебишева.
Озн.
Вираз
![]() де
a
і b
є R,
m,n,p
є Q
наз. диференц. біномом.
де
a
і b
є R,
m,n,p
є Q
наз. диференц. біномом.
Теор.(Чебишева):
Інтеграл від диференц. біному
![]() обчислюється в скінченому вигляді в
трьох наступних випадках:
обчислюється в скінченому вигляді в
трьох наступних випадках:
1) р
ціле (відємне, додатне або 0). Застосовують
підстановку
![]() де
k
– наймен.
спільний знаменник дробів m
і n.
де
k
– наймен.
спільний знаменник дробів m
і n.
2)
![]() ціле (додатне, відємне або 0). Застосов.
підст.
ціле (додатне, відємне або 0). Застосов.
підст.
![]() де
s
– знаменник
дробу
де
s
– знаменник
дробу
![]()
3)
![]() ціле (додатнє, відємне або 0). Застосов.
заміну
ціле (додатнє, відємне або 0). Застосов.
заміну
![]() де s
– знаменник
дробу
де s
– знаменник
дробу
![]()
Заув.: Чебишев довів, що у всіх інших випадках інтеграл від дифіренц. біному не вираж. у скінченому вигляді через елементарні ф-ії.
