58.Первісна ф-ії і невизн. Інтеграл.

Озн. Ф-ію F(x) наз. первісною ф-ії f(x) на (a,b). Якщо F(x) дифер. на (a,b) і F`(x)=f(x),xє(a,b). Аналогічно, враховуючи означ. одностор. похідних, визнач. первісна ф-ія на [a,b].

Прикл. Знайти первісні ф-ії :

Оскільки Зрозуміло, що ф-ія F(x)+c = також є первісною ф-ії f(x).

Наведений прикл., а також наслідок теор. про умови сталості ф-ії дозволяє зробити висновок, що коли ф-ія f(x) має первісну, то вона має також нескінчену кількість первісних, які відрізняються одна від одної на сталу.

Теор.: Якщо F(x) первісна ф-ії f(x), то множина всіх первісних ф-ії f(x) має вигляд F(x)+c, де с – довільна стала.

Озн. невизнач. інтегр. від ф-ії f(x) наз. множина всіх первісних даної ф-ії. Невизн. інтегр. познач. символом:

де знак інтегр. зміна інтегрув.

f(x) – підінтегр. ф-ія; f(x)dx – підінтегр. вираз. Якщо ф-ія f(x) має первісну, таку ф-ію наз. інтегровною, а саму задачу знаходж. перв. – інтегруванням.

Власт. Невизнач. Інтегр.:

1. Похідна від невизн. інт .= підінтегр. ф-ії:

Дов. 2. Невизн. інт. від диференц. деякої ф-ії = сумі даної ф-ії і деякої сталої:

Дов.

3. Дифер. від невизн. інт. = підінтегр. виразу:

Дов. 4. Невизн. інт. від суми (різниці) інтегровної ф-ії = сумі (різниці) невизнач. інтегр. від цих ф-ій:

5. Сталий множник можна виносити за знак інтеграла:

6. Інваріантність форми невизнач. інтегралу:

нехай а диференц. на (a,b) ф-ія. Тоді Ця властивість дуже важлива. Її зміст полягає в тому , щоб та або інша формула інтегрування зберігала свій вигляд, незалежно від того, є х – незал. змінною чи є аргументом деякої ф-ії .

Прикл.

59.Основні інтегр. Інтегр., що не є елемент. Ф-ми.

Виникає питання, якою повинна бути ф-ія, щоб вона мала первісну. Далі буде доведено, що будь-яка неперервна ф-ія має первісну. Тому домовились розглядати інтегр. від ф-ії лише в тих точках, де ці ф-ії неперервні.

Безпосередньою перевіркою можна одержати такі формули:

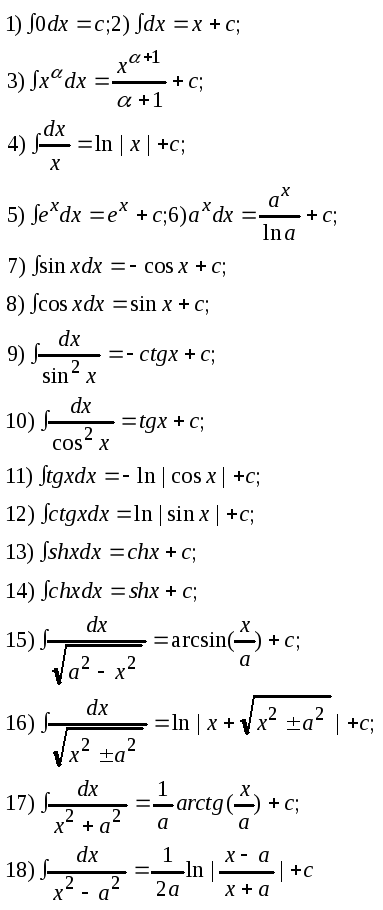Слід звернути особливу увагу на те, що інтегр. виводить нас із класу елемент. ф-ій, тобто існують такі неперервні ф-ії, первісні яких, не є елемент. Про такі інтеграли кажуть, що вони не обчислюються у скінченому вигляді або «не беруться».

Прикл. до таких інтегр. віднос.

інтегр. Пуасона

інт. Френеля

інтегральний синус, косинус.

Існують спеціальні довідники, в яких наведені, як інтеграли, що беруться так і ті, що не обчисл. в елементарних ф-іях.

60. Інтегр. Підстановкою у невизн. Інтегр. Приклади.

Цей метод базується на наступн. теор. і суть його полягає у введені нової змінної інтегруван.

Теор.: Нехай ф-ія F(x) первісна ф-ії f(x) на деякому інтерв. (a,b) і диференц. ф-ія визначена на інт. , коли t змінюється на .

Довед. Розглянемо ф-ію

Це складна ф-ія за правилом диференц. складної ф-ії:

Наведена теорема використовується у наступних двох методах:

1) розгляд. у вигляді:

= зроб. заміну.

2) Якщо в інтегр. , диференц. і існує обернена ф-ія то інтегр.

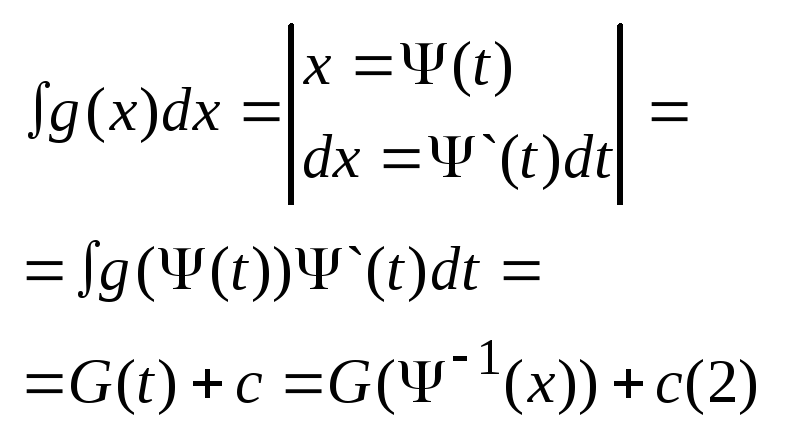
Розглян. форм.(1) і (2). У форм.(1) ідеться про внесення ф-ії під знак інтегр. У форм.(1) йдеться про внесеня ф-ії під знак інтегр., а у форм.(2) ф-ія виноситься з-під знаку інтегралу Загального правила, яким з двох методів користуватися взагаліне існує. При застосув. форм. (1) і (2) слід виходить з того, щоб одержана після перетворень підінтегральна ф-ія мала більш простий вигляд.

Заув. При інтегруванні методом заміни змінної слід обовязково повертатися від нових змінних u і t у первісній до старої змінної х.

Приклад 1:

Приклад 2: