34.Похідні елемент. Ф-ій

Теорема 1

Похідна від сталої дорівнює 0.

с’ = 0.

Доведення:

Якщо f(x)=c,x, то f(x+)=c, f’(x) =

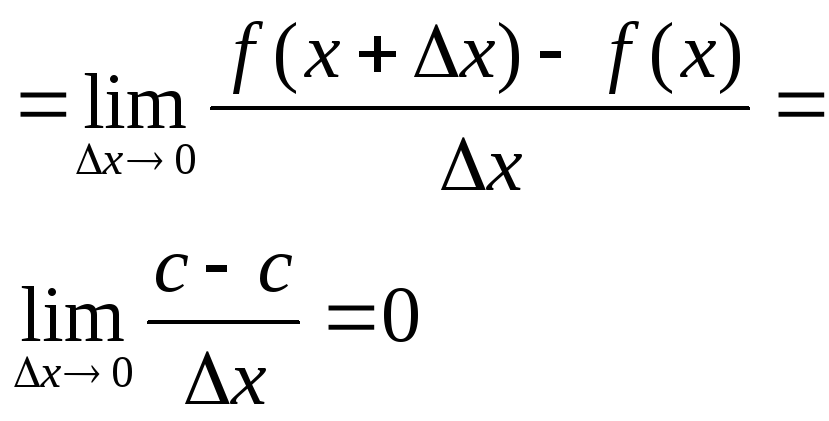
Теорема 2

Сталий множник можна виносити за знак похідної. (cu)’=cu’

Доведення:

За теоремою 1 і теоремою про границю добутку одержемо: (cu)’ = c’u+cu’ = 0+cu’=cu’

Теорема 3

Похідну степеневої функції знаходять за формулою

Доведення:

Використаємо еквівалентність

еквівалентно . За означенням похідної:

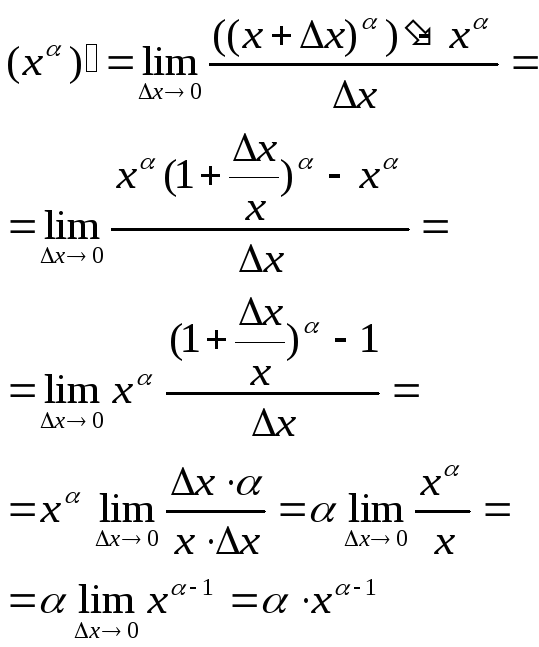
Теорема 4

Похідні тригонометричних функцій знаходять за формулами

1.

_2.

_3.4.

Доведення:1.За означенням похідної

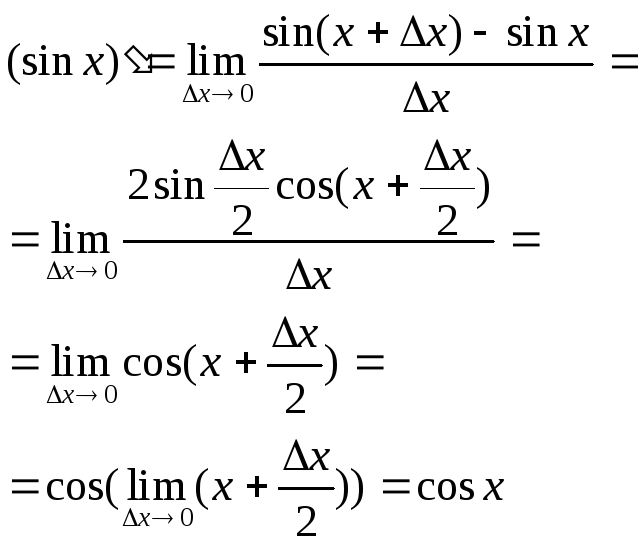
Оскільки cosx неперервна функція ми застосували правило граничного переходу

2.

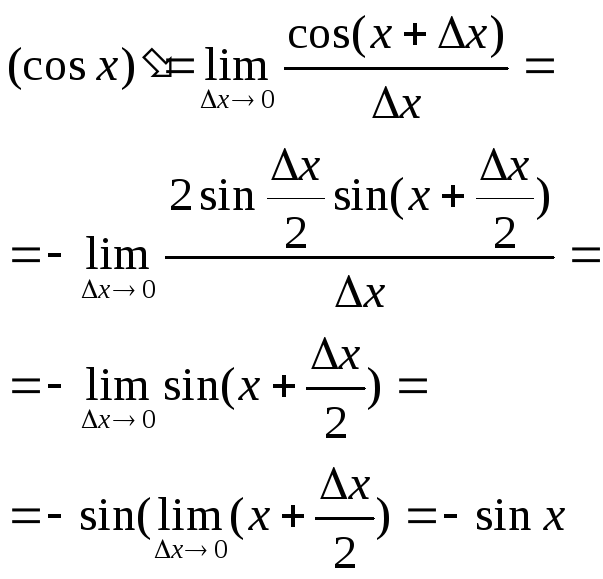
Оскільки sinx неперервна ф-ія ми застосували граничний перехід.

3.

4.

Теорема 5

Похідну показникової функції знаходять за формулою

Доведення:

Використовуємо еквівалентність: еквівалентна , . За означенням похідної

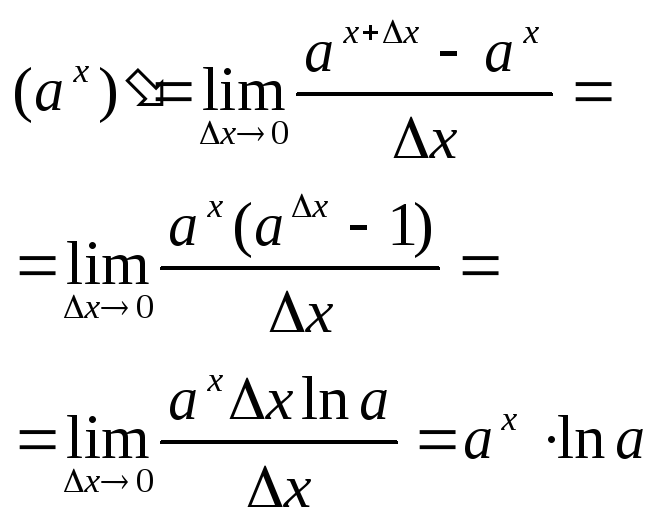
Наслідок:

Теорема 6

Похідну логаріфмічної функції знаходять за фомулою: .

Доведення:

Використовуємо еквівалентність: еквівалентна . За означенням похідної:

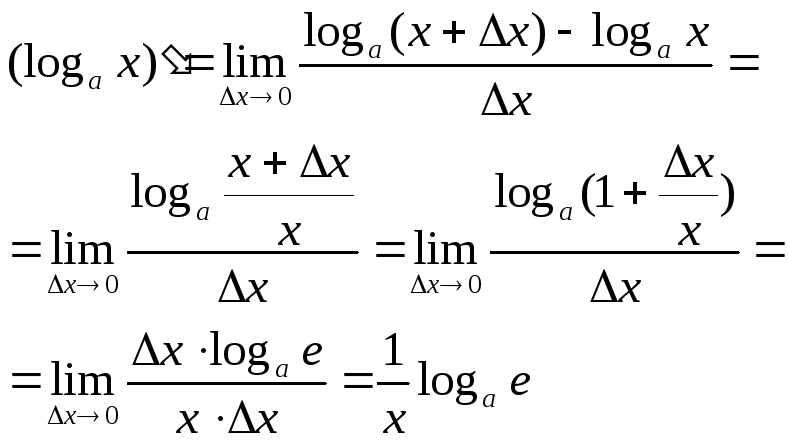
Наслідок:

35.Похідна складної функції. Похідна функції заданої неявно.

Нехай , -визначає складну ф-ію.

Теорема:

Якщо ф-я в т.х, а ф-я дифіренційовна у відповідній U, то складна функція має похідну в точці Х і справедлива формула

Доведення

Оскільки ф-ія дифіренц. точці U, то існує границя

За теоремою про існування границі в точці ф-ії

, де -нескінченно мала, , якщо

Звідси

(1)

Оскільки за умовою ф-ія , диференційовна в точці х, то існує границя

Аналогічно , де , якщо

Оскільки рівняння

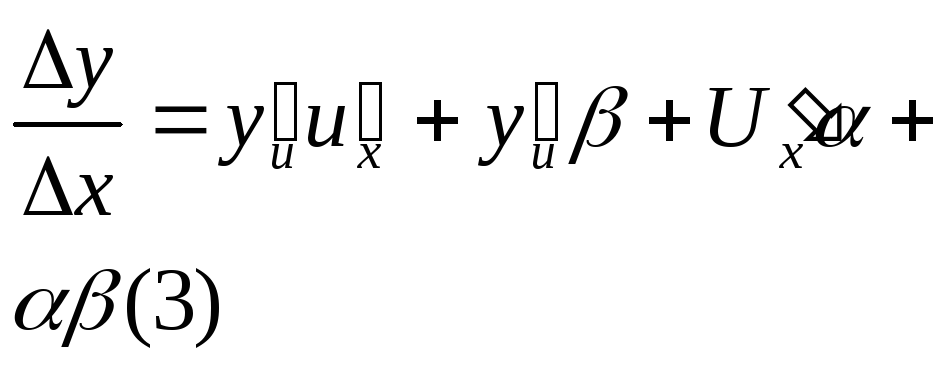
диференційовне в точці х, то за теоремою вона є неперервною в цій точці

за означенням неперервності

Таким чином, якщо , то ,

, одержимо

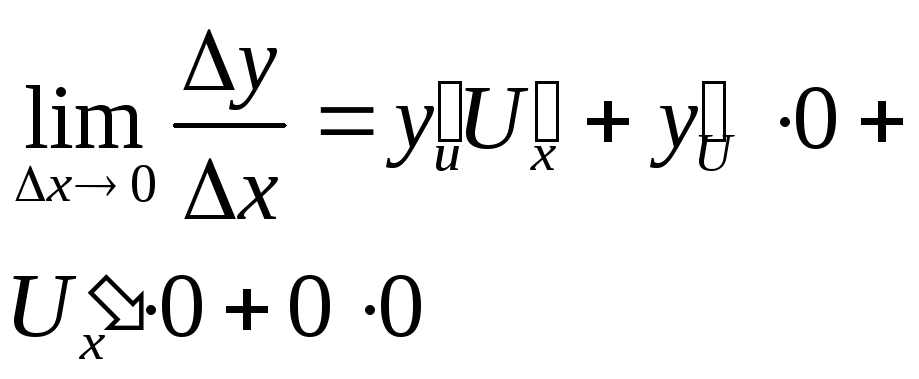
Теорема доведена.

Означення

Якщо ф-ія задана рівнянням , розв’язаними відносно залежної змінної, то таку ф-ію називають явною, під неявним завданням ф-ії розуміють F(x,y)=0, які не можна розв’язати відносно у.

- задана неявно.

Нехай -задана рівнянням F(x,y)=0 (4)

Щоб продиф. Неявну функцію необхідно взяти похідну від обох частин рівності (4) вважаючи, при цьому y-це функція від х.

Потім одержане рівняння розв’язати відносно , похідна неявної функції таким чином буде виражатись через у та х.

36. Похідна оберн. Ф-ії. Диференц. Оберн. Тригоном. Ф-ій.

Нехай ф-ія y=f(x) визначена на деякій множ. Х і має обл. значень множ. У. Може статися, що різним значен. х відповід. одне значен. ф-ії.

У цьому питані ми будемо розглядати лише такі ф-ії для яких різним значен. аргумента х відповід. різні значен. ф-ії

Для таких ф-ій можна стверджув., що уєУ відповідає єдине значення х є Х, тобто на множині У задана ф-ія Цю ф-ію наз. оберненою до ф-ії y=f(x). Її позначають також символом

ОЗН.1. Нехай y=f(x) ф-ія визначена на множ. Х. Якщо ф-ію f(x) наз. зростаючою.

ОЗН.2. Якщо ф-ію f(x) наз. незростаючою.

ОЗН.3. Якщо ф-ію f(x) наз. спадною

ОЗН.4. Якщо ф-ію f(x) наз. неспадною.

Всі перечислені озн. наз. монотоними, а зрост. і спадна ф-їя наз. строго монотон.

ТЕОР.1.(про існув. і похідну обернен. ф-ії) Якщо ф-ія y=f(x) строго монотона на (a,b) і во всіх його точках має відмінну від 0 похідну f `(x), то існує обернена ф-ія похідну якої можна знайти за форм. або .

ТЕОР.2.(похідні обернених тригоном. ф-ій) Довед. (1) ф-ія y=arcsinx є оберненою до ф-ії x=siny. В свою чергу ф-ія x=siny зростає на і має відмінну від 0 похідну Тоді за теор.1 с форм. (1)