Практическая работа № 2 установление вида зависимости между двумя переменными величинами

Иногда необходимо выяснить вид зависимости между двумя переменными величинами, которая может быть функциональной или стохастической.

Функционально зависимыми являются такие величины, у которых каждому значению одной величины соответствует вполне определенное (чаще всего одно) значение другой величины (величина износа резца от времени, зависимость давления от температуры, величина погрешности размера изделия от температуры, свойства сплавов от процентного содержания в нем того или другого элемента и др.).

Стохастически зависимыми называются такие величины, у которых различным значениям одной величины соответствуют различные законы распределения другой величины. Частным случаем стохастической зависимости является коррелятивная зависимость. Она появляется в том случае, когда каждому значению одной величины соответствуют различные средние значения другой величины (размеры изделий обрабатываемых одновременно на одном станке, одним инструментом, в одном приспособлении и др.).

Остановимся на выравнивании эмпирических данных по некоторым видам функциональных зависимостей и на методике определения коэффициента корреляции при коррелятивной зависимости.

Для установления вида функциональной зависимости эксперимент проводится таким образом, что для каждого значения одного признака (независимое переменное х) определяется значение другого признака (зависимого переменного y ), а результаты заносятся в таблицу вида

№	1	2	3	...	n
Температура xi	xi	x2	x3	...	xn
Размер изделия yi	yi	y2	y3	...	yn

По этим данным строится график зависимости между величинами х и y. Полученную ломаную линию выравнивают по наиболее близкой к ней теоретической кривой.

1. Функциональная зависимость

Требуется найти функцию у=f(x), значения которой при возможно меньше отличались бы от эмпирических значений . В основу решения положен принцип Лежандра, по которому сумма квадратов отклонений эмпирических значений y от у_i определяемых по формуле, должна быть наименьшей. Так как большинство функций может быть представлено в виде многочлена n-й степени, то при выравнивании целесообразно представлять зависимость между переменными величинами в виде параболы n-й степени:

y = a_ + a_x + a_x^ + ...+ a_nxⁿ ,

где a_, a_, a_,..._, a_n - неизвестные параметры. Для их нахождения воспользуемся интерполяционной формулой Чебышева [*], которая имеет вид: y = k_q_(x) + k₁q₁(x) + k₂q₂(x) + ...+ k_q_(x). Здесь величина характеризует порядок параболы; - число значений независимой переменной. В этой формуле аргументом является величина , где .

Последовательность вычисления и способы определения входящих в интерполяционную формулу коэффициентов покажем на примере (см. табл. 13).

Таблица 13

№	Функ-ция уi	Аргу-мент иi	у2i		уixi	x2i	x2i yi	x3i	x4i	x3i yi	x5i	x6i
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1 2 3 4 5 6 7 8 9	2 10 17 33 51 66 96 120 172	1 3 4 6 7 8 10 11 13	4 100 289 1089 2601 4356 9216 14400 29584	-6 -4 -3 -1 0 +1 +3 +4 +6	-12 -40 -51 -33 0 +66 +288 +480 +1032	36 16 9 1 0 1 9 16 36	72 160 153 33 0 66 864 1920 6192	-216 -64 -27 -1 0 1 27 64 216	1296 256 81 1 0 1 81 256 1296	-482 -640 -459 -33 0 66 2592 7680 37152	-7776 -1024 -243 -1 0 1 729 4096 46656	46656 4096 729 1 0 1 729 4096 46656	2,9 9,6 16,3 35,6 48,5 63,5 99,8 121,2 170,3	2,1 13,1 20,6 37,7 48,4 61,2 95,3 117,6 175,3
Сумма	567	63	61639		1730	124	9460	0	3268	-1564 +47490 45926	0	102964

О п р е д е л е н и е п а р а б о л ы н у л е в о й с т е п е н и

Находим и заносим ее в конце колонки 2 (табл. 13).

Определяем величину . Она равна.

Для уравнения параболы нулевого порядка .

Находим уравнение параболы нулевого порядка

.

Определяем основную ошибку. Для этого находим и заполняем колонку 4. Вычисляем, что . Находим величину .

Основная ошибка равна

.

О п р е д е л е н и е п а р а б о л ы п е р в о г о п о р я д к а

Вычисляем .

Вычисляем .

Заполняем колонку 5, вычисляя значения .

Заполняем колонку 6, вычисляя произведения и находим.

Заполняем колонку 7, вычисляя и находим

Вычисляем уравнение параболы первой степени.

Вычисляем

Для параболы 1-го порядка величина. Поэтому.

Складываем.

Искомое выражение .

Вычисляем основную ошибку

Так как значительно превосходит , то необходимо продолжить интерполирование.

О п р е д е л е н и е п а р а б о л ы в т о р о г о и т р е т ь е г о п о р я д к а

Вычисляем произведение , заполняем колонку 8 и находим, что 9460.

Вычисляем , заполняем колонку 9 и находим, что .

Вычисляем , заполняем колонку 10 и находим, что .

Вычисляем величины

.

.

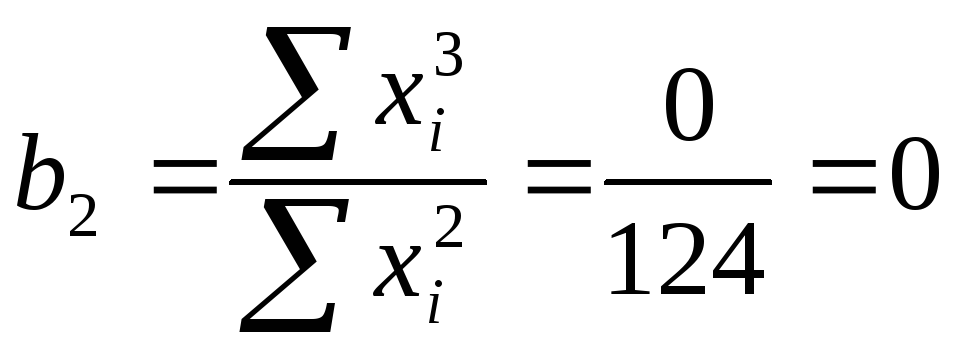Вычисляем величину,

Складываем и получаем уравнение параболы второго порядка

Вычисляем основную ошибку

;

Если полученное значение считать достаточно малым, то можно ограничиться вычислением параболы 2-го порядка. После этого необходимо перейти от аргумента к аргументу u, подставив в уравнение параболы 2-го порядка x=u - 7.

Тогда окончательно получим

или

Для примера выполним вычисление параболы 3-го порядка.

Вычисляем произведения , заполняем колонку 11 и находим = 45926.

Вычисляем , заполняем колонку 12 и находим, что .

Вычисляем , заполняем колонку 13 и находим, что .

Вычисляем выражения

;

;

;

;

.

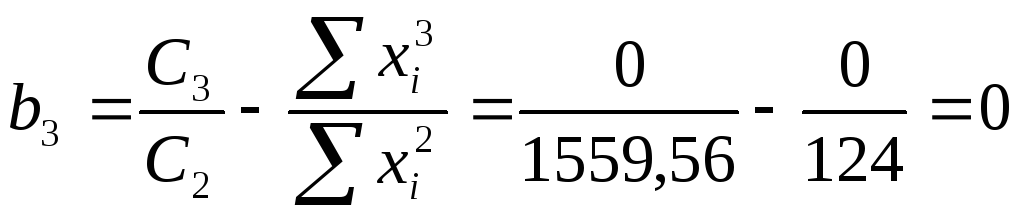Определяем

;

;.

Вычисляем уравнение параболы 3-го порядка

.

Вычисляем основную ошибку

;

Так как , то, следовательно, выравнивание по параболе 3-го порядка дает несколько лучшее приближение. Величина мало отличается от и поэтому дальнейшее увеличение порядка параболы нецелесообразно.

Следует также отметить, что в практических случаях параболы выше 3-го порядка встречаются очень редко и дают практически несущественное уменьшение основной ошибки.

Выразим аргумент х функции через аргумент . Для этого вместо х подставим как и ранее () в

В колонках 14 и 15 приведены выравненные значения у, высчитанные по параболам 2-й и 3-й степени.