6. Функции плотности теоретических и эмпирических распределений

Подбор теоретической функции для эмпирического распределения

Рассмотрим случай, когда эксперимент проводится с целью установления вида функции плотности вероятности. Априори эта функция неизвестна и можно лишь предположительно судить о ее виде. Обработка результатов экспериментальных наблюдений производится в следующей последовательности:

а) по опытным данным строится эмпирическая кривая;

б) определяются параметры эмпирического распределения;

в) выдвигается одна или несколько гипотез о функции плотности исследуемой случайной величины, исходя из внешнего вида экспериментальной кривой, из значений ее параметров и технологических факторов, влияющих на ее вид;

г) эмпирическая кривая выравнивается по одной или последовательно по нескольким принятым теоретическим кривым;

д) проводится сравнение по одному из критериев согласия эмпирической и теоретической (выровненной эмпирической) кривых;

е) выбирается функция, дающая наилучшее согласование.

2. Выравнивание эмпирического распределения по гипотетическим теоретическим

Общее правило выравнивания состоит в следующем.

В каждое теоретическое распределение ( в его дифференциальную или интегральную функции) входит несколько величин, называемых параметрами ( математическое ожидание, дисперсия и др.). Так как эти величины априори неизвестны, то их необходимо определить по эмпирическому распределению, подставить в функцию плотности вместо теоретических значений этих величин, а затем рассчитать вероятности середин всех интервалов. Умножив эти вероятности на число опытов, получим теоретические значения частот случайной величины, которые дают выровненную кривую. Для примера рассмотрим выравнивание эмпирического распределения по нормальному закону (Гаусса).

Данный закон двухпараметрический. Поэтому предварительно необходимо вычислить среднее значениеи среднее квадратическое отклонение .

Для вычисления воспользуемся данными, приведенными в табл. 5.

Определяем = -0,0284 и S= 0,0515.

Подставляем эти значения в функцию плотности (12), заменяя на и на .

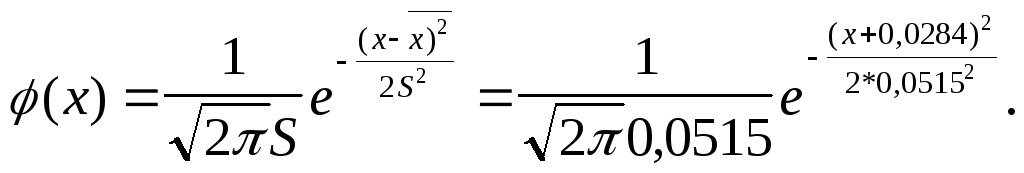
Результаты выравнивания приведены в табл. 10. Сделаем некоторые пояснения к этой таблице.

В колонке 5 определяется ,

где - середина i-го интервала;

- среднее значение;

- среднее квадратичное отклонение.

По вычисленным значениям в приложении 1 находим значения , которые проставляются в колонке 6.

Таблица 10

Номер интервала (№)	Середина интервала x_i	Эмпирические частоты m_i				Вероятность интервалов	Теоретические частоты m_i
1	2	3	4	5	6	7	8
1 2 3 4 5 6 7 8 9 10 11 12 13 14	-0,14 -0,12 -0,10 -0,08 -0,06 -0,04 -0,02 0,00 0,02 0,04 0,06 0,08 0,10 0,12	3 8 11 20 27 36 29 18 17 17 8 4 1 1	-0,1116 -0,0916 -0,0716 -0,0516 -0,0316 -0,0116 0,0084 0,0284 0,0484 0,0684 0,0884 0,1084 0.1284 0,1484	-2,17 -1,78 -1,39 -1,00 -0,61 -0,23 0,16 0,55 0,94 1,33 1,72 2,10 2,49 2,88	0,0379 0,0818 0,1736 0,2420 0.3332 0,3885 0,3939 9,3429 0,2565 0,1647 0,0909 0,0440 0,0180 0,0063	0,01472 0,03177 0,06742 0,09398 0,12940 0,15087 0,15297 0,13317 0,0996 0,07396 0,.03530 0,.01709 0,00699 0,0063	2,94 6,35 13,48 18,80 25,88 30,17 30,59 26,63 19,92 14,79 7,06 3,42 1,40 0.49
Сумма		200					200