В) Результаты эксперимента заданы выборкой небольшого объема. Объем выборки n  25

В тех случаях, когда объем выборки невелик, значения случайной величины делить на интервалы нецелесообразно. Определять моменты 3-го и 4-го порядков в этом случае также нецелесообразно, так как они имеют большую дисперсию и при малых выборках по ним трудно судить о величине соответствующих параметров генеральной совокупности.

Пусть в результате эксперимента получены следующие значения случайно величины:х₁, х₂, х₃...., х_N.

Среднее значение и дисперсия определяются по формулам

Рассмотрим пример.

Имеем следующие значения выборки:

х_i = 9,77; 9,76; 9,79; 9,78; 9,82; 9,77; 9,78.

Вычисляем

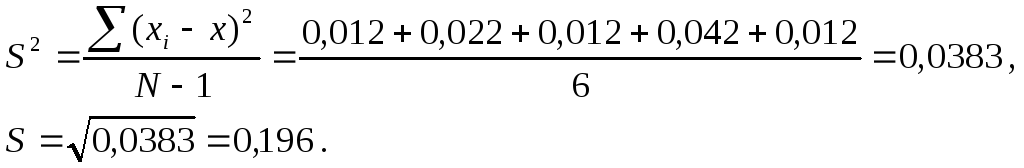
3. Методика определения поля допуска по эмпирическому распределению

Многие эксперименты проводятся с целью определения поля допуска, которое характерно для данного технологического процесса и дает вероятность риска (брака) не более некоторого наперед задаваемого числа. Эту вероятность будем в дальнейшем обозначать через 2. Обычно принимают 2 = 0,0027. Математическое ожидание и дисперсия априори (до опыта) неизвестны, а имеется лишь возможность получить из выборки значения и S², которые являются оценками для МХ и DX.

В этом случае принимать за поле допуска величину размаха R нельзя, так как практически предельное поле рассеивания в общем случае никогда не равно размаху.

Если же за поле допуска принимать значение , то границы поля допуска будут колебаться от одной выборки к другой, и в одних случаях они будут охватывать более 99,73% всей площади, ограниченной кривой, в других - менее, так как х и S являются случайными величинами.

Задача состоит в том, чтобы выбранное поле допуска охватывало не менее 99,73% всей площади, ограниченной генеральной кривой (или некоторого другого заранее задаваемого числа). Для этого следует найти такое l, чтобы с задаваемой вероятностью, близкой к единице (надежностью Р), содержало не менее (1 - 2) 100% всей нормальной генеральной совокупности.

В табл. 7 приведены значения l, вычисленные для надежностей Р = 0,9; 0,95; 0,99 и для случаев, когда интервал будет охватывать не менее 99,73; 95 и 90% всей генеральной совокупности [*], где , S - эмпирическое среднее и среднее квадратическое отклонение.

Значения коэффициента l рассчитаны для выборки из нормальной совокупности.

Рассмотрим пример определения поля допуска.

Для эмпирического распределения определяем и S.

Для данных табл. 5 получили: = - 0,284; S = 0.0515; k = N - 1 = 200 - 1 = 199,

где k - число степеней свободы.

Задаемся надежностью определения допуска. Положим, что Р = 0,9. Задаемся вероятностью 1 - 2, т. е. задаем площадь генеральной кривой, которая входит в определяемый нами допуск.

Положим 1 - 2 = 1 - 2 ^. 0,00135 = 0,9973.

По табл. 7 находим, что для Р = 0,9

1 - 2 = 0,9973 и k = N - 1 = 199 (принимаем k = 200). Отсюда l = 3,40.

____________________________________

* Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике, М. Гостехиздат, 1955.

Определяем границы поля допуска:

t₁ = - l S = -0,0282 - 0,0515 ^. 3,40 = -0,2033,

t₂ = + l S = -0,0282 + 0,0515 ^. 3,40 = 0,1469.

Таблица значений l для определения гарантированного поля допуска

Таблица 7

k= N-1 число степеней свободы	Надежность Р = 0,9			Надежность Р = 0,95			Надежность Р = 0,99
	1 - 2			1 - 2			1 - 2
	0,9973	0,95	0,9	0,9973	0,95	0,9	0,9973	0,95	0,9
4 5 6 7 8 9 10 12 14 16 18 20 25 30 40 50 60 70 80 90 100 200 300 400 500 600 800 1000	6,76 6,07 5,60 5,80 5,07 4,89 4,75 4,54 4,39 4,28 4,19 4,11 3,98 3,89 3,78 3,69 3,63 3,59 3,55 3,53 3,51 3,40 3,35 3,32 3,30 3,29 3,27 3,26	4,18 3,74 3,47 3,27 3,13 3,02 2,94 2,81 2,72 2,65 2,59 2,54 2,46 2,40 2,33 2,28 2,25 2,22 2,20 2,18 2,17 2,10 2,07 2,06 2,05 2,04 2,03 2,02	3,51 3,14 2,91 2,75 2,63 2,54 2,47 2,36 2,28 2,22 2,17 2,14 2,07 2,02 1,95 1,91 1,89 1,86 1,85 1,83 1,82 1,76 1,74 1,73 1,72 1,71 1,70 1,70	8,26 7,17 6,50 6,05 5,72 5,48 5,28 4,99 4,78 4,62 4,50 4,39 4,20 4,10 3,94 3,84 3,76 3,70 3,66 3,63 3,60 3,47 3,41 3,37 3,35 3,33 3,30 3,29	5,11 4,44 4,02 3,74 3,54 3,39 3,26 3,08 2,96 2,86 2,79 2,72 2,61 2,54 2,44 2,37 2,33 2,30 2,27 2,25 2,23 2,14 2,11 2,08 2,07 2,06 2,05 2,04	4,29 3,72 3,38 3,14 2,97 2,84 2,74 2,59 2,49 2,40 2,34 2,29 2,19 2,13 2,05 1,99 1,96 1,93 1,91 1,89 1,87 1,80 1,77 1,75 1,74 1,73 1,72 1,71	12,80 10,31 8,91 8,01 7,38 6,91 6,55 6,03 5,67 5,41 5,21 5,05 4,76 4,57 4,31 4,15 4,05 3,96 3,90 3,84 3,80 3,59 3,50 3,45 3,41 3,39 3,36 3,33	7,92 6,38 5,51 4,95 4,56 4,27 4,05 3,73 3,52 3,35 3,22 3,12 2,94 2,82 2,67 2,57 2,50 2,45 2,41 2,38 2,35 2,22 2,17 2,14 2,12 2,10 2,08 2,07	6,64 5,35 4,62 4,15 3,83 3,59 3,40 3,13 2,95 2,81 2,70 2,62 2,47 2,37 2,24 2,16 2,10 2,06 2,02 2,00 1,98 1,87 1,82 1,79 1,78 1,76 1,75 1,74

Находим координату середины поля допуска и половину поля допуска:

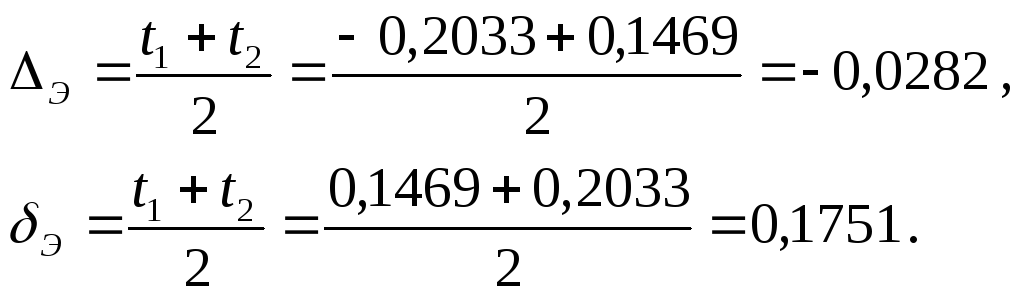
Таким образом, если за поле допуска брать величину t₂ - t₁ = 0,3502, то с вероятностью 0,9 из всех будущих наблюдений 99,73% будут лежать в этом интервале.