1. Основные параметры, характеризующие пластическую деформацию в условиях сверхпластичности

В условиях изотермической деформации истинное напря­жение пластического течения σ является функцией сте­пени ε и скорости деформации: .

В дифференциальной форме эта зависимость имеет вид

.

Здесь во втором слагаемом характеризует чувст­вительность напряжения течения к скорости деформа­ции.

Принимая, что малые изменения а линейно зависят от малых изменений ε и , можно выразить связь меж­ду σ, ε и так:

(192а)

разделив это выражение на dt, получим

(193)

Скорость деформации

(194)

где А — поперечное сечение. Знак минус связан с тем, что знак изменения А обратен знаку изменения длины образца:

(195)

Однако сила, вызывающая деформацию, равна

(196)

а изменение ее во времени . Разделив друг на друга последние два равенства , под­ставим в правую часть соответствующие значения из вы­ражений (193) — (195) и введем обозначения

и (197)

(198)

При этом получим

(199)

Анализ выражения (199) при разных граничных усло­виях дает важную информацию о физическом смысле коэффициентов и .

Так, подставляя в уравнение (197) значение из (192а), имеем

Для случая, когда материал нечувствителен к скорости деформации, второй член равен нулю и , где имеет смысл показателя упрочнения .

Следовательно, — параметр материала, описываю­щий чувствительность показателя к деформации, т. е. склонность материала к упрочнению при деформации.

Аналогично, подставляя в уравнение (198) значение из (192а), имеем

(200)

Для случая, когда материал не упрочняется при деформации (что соответствует условиям вязкого течения и сверхпластичности), второй член равен нулю и

(201)

Следовательно, — параметр материала, описываю­щий чувствительность напряжения пластического тече­ния к скорости деформации, т. е. склонность материала к упрочнению при увеличении скорости деформации.

Суммарная зависимость упрочнения материала от степени деформации и от ее скорости может быть запи­сана с помощью параметров и для случая равно­мерной деформации так:

(202)

Эта зависимость, называемая уравнением состояния те­ла с вязкопластическими свойствами, характерна дву­мя крайними случаями:

а) зависимость σ от степени деформации пренебрежи­мо мала (n→0). Тогда

(203)

Материал ведет себя как вязкий, т. е. максимально пластичный, в случае m=1 наблюдается прямая про­порциональность между σ и ε (так называемое ньюто­новское поведение);

б) зависимость σ от скорости деформации пренебре­жимо мала (m→0). Тогда .

Материал ведет себя как идеально пластичное тело, упрочнение которого определяется степенью деформации.

Подстановка в зависимость (203) соответствующих значений из выражений (194) и (196) позволяет полу­чить зависимость скорости изменения площади сечения dA/dt от значения А и параметра m. Она имеет вид

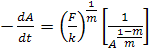
На рис. 289 показана эта зависимость в координатах dA/dt—А для разных значений m. Видно, что для раз­ных m зависимость носит разный характер. При малых т (0,2—0,4) и n=0 скорость изменения площади сечения резко зависит от величины этой пло­щади и тем резче, чем меньше т. Значит, при малых т возникающая неоднородность сечения (локальное утоне­ние) будет резко усиливаться в процессе дальнейшей де­формации.

С ростом m чувствительность к неодородностям ос­лабевает и при m=1 скорость изменения сечения пере­стает зависеть от неоднородностей в величине А.

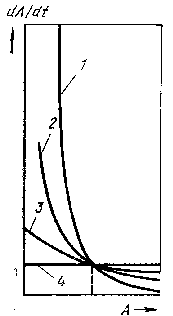
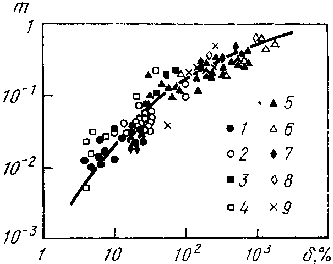
Рис. 289. Зависимость скорости из­менения площади сечения от вели­чины этой площади для разных значений параметра т:

1 —m-0,25; 2 — 0,5; 3 — 0,75; 4-1

Рис. 290. Зависимость между экспери­ментально найденным максимальным удлинением и величиной т:

1—9 — данные разных авторов

Таким образом, величина т характеризует склон­ность материала к образованию шейки, а значит и склон­ность к сверхпластичности.

На рис. 290 приведена зависимость между экспери­ментально найденными значениями максимального от­носительного удлинения δ, %, характеризующего макси­мальную пластичность, и величиной т. Видно наличие определенной корреляции. Сверхпластичность проявля­ется у сплавов, для которых m>0,3. Обычную пластич­ность обнаруживают материалы, для которых m<0,2.

Однако, как показано во многих работах, один и тот же материал при неизменном т обнаруживает разное удлинение δ, %, в зависимости от величины зерна и характера структурных изменений в ходе самой деформации.

Таким образом, высокое значение т, т. е. высокая чувствительность напряжения течения σ к скорости де­формации , является необходимым, но недостаточным условием проявления сверхпластичности.

В настоящее время нет единого критерия, который мог бы однозначно характеризовать склонность мате­риала к сверхпластичности.

Поэтому для суждения о пластичности материала и склонности его к сверхпластичности, кроме величины т, следует определять и другие характеристики. Наиболее полезную информацию дают значения относительного максимального удлинения δ ,%, а также данные о протяженности стадии стабильной деформации на истин­ных диаграммах растяжения.

Что касается внешних проявлений сверхпластичности, кроме высокого значения т, то к ним следует отнести еще равномерное удлинение образца без образования шейки, а также очень небольшое упрочнение в процессе деформации, проходящее через максимум на начальных стадиях деформации.

Значение параметра т определяют из данных о ме­ханических испытаниях на растяжение.

При использовании жесткой машины наиболее рас­пространен метод скачкообразного изменения скорости растяжения (метод Бэкофена и его модификации). По методу Бэкофена скорость деформации изменяется соот­ветствующим изменением нагрузки F. Однако после из­менения нагрузки установившееся течение достигается по прошествии определенного времени. Поэтому непо­средственно из диаграмм растяжения значение т опре­делить нельзя. Обычно прибегают к экстраполяции за­висимости для получения значений одинаковой степени деформации при разных скоростях растяжения.

На рис. 291 схематически показана кривая нагруз­ка — время, получаемая с помощью жесткой машины для случая, когда в момент времени, соответствующий точке D, скорость растяжения мгновенно увеличили от от υ₁ до υ₂. Установившемуся состоянию после увеличе­ния нагрузки соответствует точка А.

Для определения параметра т экстраполируют ли­нию установившегося течения от точки С при меньшей скорости υ₁ до точки В, соответствующей такой же де­формации, какая получена при большей скорости растя­жения в точке А. Затем из графика находят усилия, со­ответствующие точкам А и В, и, пренебрегая небольшим изменением параметра т в области экстраполяции, оп­ределяют его значение из зависимости

(204)

где и — нагрузки при соответствующих скоростях υ₂ и υ₁.

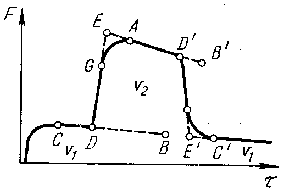
Рис. 291. Кривая нагрузка — время для растяжения со скачкообразным изменением скорости растяжения υ₁ и υ₂> υ₁, используемая для опре­деления параметра т.

Улучшенные варианты расчета позволяют избежать влияния на значение параметра m тех структурных из­менений, которые могут быть вызваны в материале уве­личением усилия F и соответственно скорости деформа­ции. Это изменение режима деформации должно вызвать повышение плотности структурных дефектов, что в свою очередь должно изменить постоянную m и значение n в уравнении (202).

Чтобы избежать влияния структурных изменений, целесообразно определить значение m из усилий, соот­ветствующих не точкам А и В, а точкам G и D (см. рис. 304), тогда

(205)

Физический смысл этой замены заключается в следу­ющем. Мгновенное изменение напряжения от точки D к точке G при изменении скорости деформации характеризует сопротивление деформированию для двух данных скоростей деформации при минимальном различии в сте­пени деформации, т. е. при минимальном различии в структуре.

Как показывает сопоставление данных разных авто­ров, значения т, полученные с помощью зависимостей (204), дают завышенные и часто не повторяющиеся зна­чения. Зависимость (205) дает меньшие по величине и лучше сходимые результаты.