§ 3-5. Связь между различными динамическими характеристиками

Как уже указывалось выше, все рассмотренные динамические характеристики являются полными, и применение любой из них в каждом конкретном случае является исключительно делом вкуса или удобства. Каждая из характеристик может быть однозначно найдена, если известна любая другая характеристика (рис. 3-6). Рассмотрим этот вопрос подробнее.

Стационарная линейная система или элемент системы с сосредоточенными параметрами описывается обыкновенным дифференциальным уравнением с постоянными коэффициентами

(3-26)

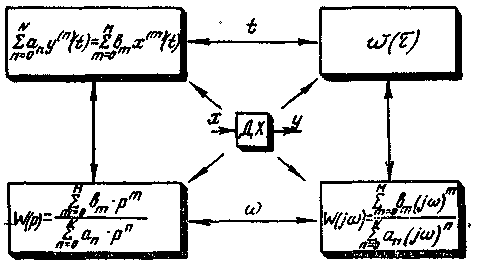
Рис. 3-6. Взаимосвязь динамических характеристик

(сравни с (3-13)). Импульсная характеристика w(t)(или переходная функция вh(t)) может быть найдена как решение этого уравнения для нулевых начальных условий при подстановкех(t)=δ(t)(илих(t)=1(t) дляh(t)). Для определения передаточной функции по (3-26) воспользуемся теоремой о дифференцировании оригинала при нулевых начальных условиях (см. табл. 3-1, п. 5). Получаем аналог (3-26)

, (3-27)

откуда, вынося Y(р)иХ(р) за знак суммы, получаем в соответствии с определением (3-22)

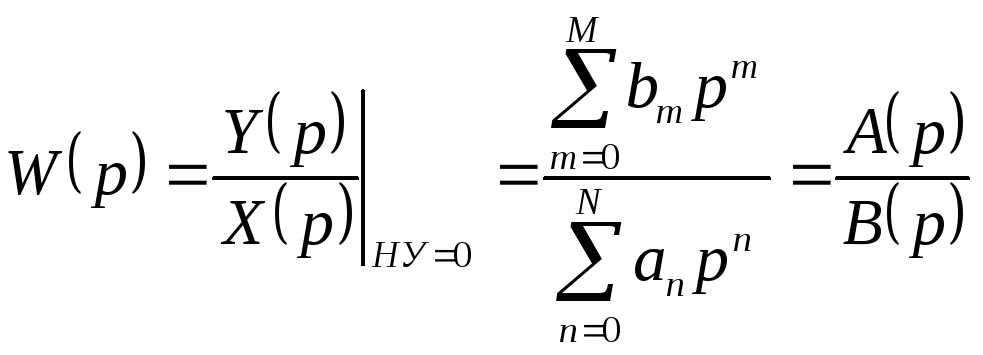. (3-28)

Таким образом, передаточная функция линейных систем с сосредоточенными параметрами всегда является дробно-рациональной функцией. Из связи преобразований Лапласа и Фурье получаем

. (3-29)

Таким образом, переход от характеристик во временной области (3-26) к характеристикам в частотной области (3-29) не представляет труда. Для обратного перехода, например, от передаточной функции (3-28) к дифференциальному уравнению (3-26) следует лишь произвести подстановку в (3-27) (оператор дифференцирования) .

Импульсная характеристика может быть найдена из передаточной функции как обратное преобразование Лапласа

, (3-30)

где с — абсцисса абсолютной сходимости.

На практике вместо преобразования (3-30) пользуются для дробно-рациональных функций типа (3-28) теоремой разложения Хевисайда (эта теорема для случая простых корней дана в табл. 3-1, п. 9)

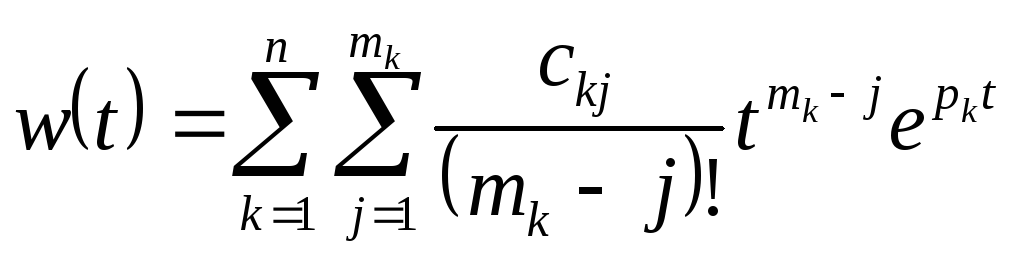, (3-31,а)

где p_k— корни алгебраического уравненияА(р)=0;

п— числоразных корней уравненияА(р)=0;

т_k — кратность корняp_k(очевидно, что)

c_kj- — коэффициент, находимый как

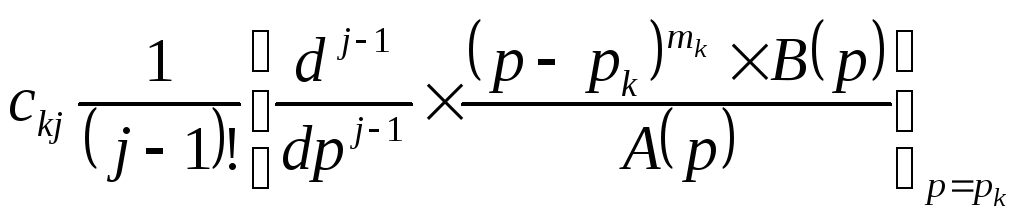. (3-31б)

Пример 3-4. Рассмотрим дифференциальное уравнение двигателя (3-10) приМ_с=0. Передаточная функция, как следует из (3-28), равна

.

Корни уравнения А(р)=0 простые и равныр₁=0,. По теореме разложения (удобнее в форме п. 9 табл. 3-1) находим

Глава 4 структурный метод анализа сар

Составление дифференциальных уравнений даже простых динамических систем — сложная задача. Подобно тому как любая конструкция состоит из нескольких более простых элементов, так и всякая САР может быть представлена состоящей из ряда простейших связанных друг с другом элементов — звеньев системы автоматического регулирования. Надо заметить, что при изображении САР применяют два типа схем — функциональные и структурные. Обычно после составления функциональной схемы переходят с целью анализа САР к ее структурной схеме, которая позволяет выявить основные свойства САР, провести анализ устойчивости и качества процессов регулирования, а при необходимости — и провести коррекцию системы.