Примеры решения задач

Задача 1. Два источника с=1,4 В и =1,1 В и внутренними сопротивлениями соответственно =0,3 Ом и =0,2 Ом замкнуты разноименными полюсами (рис.21). Определить разность потенциалов между точками 1 и 2.

Дано: Решение

=1,4 В 1. В основе решения лежит закон

=1,1 В Ома в интегральной форме для

=0,3 Ом неоднородного участка цепи

=0,2 Ом .

рис.21 Рис. 21

2. Так как в схеме нет узлов, то ток во всех участках цепи один и тот же.

Применим указанные выше правила знаков для неоднородного участка 1--2 и запишем для него закон Ома. Выберем обход участка по часовой стрелке, то есть от точки 1 к точке 2. На этом участке направление тока противоположно направлению обхода, вектор также имеет направление, противоположное обходу. Следовательно, чтобы применить формулу (5.1) для данного участка, перед силой тока и перед ЭДС нужно поставить знак минус:

-. (1)

3.Применим тот же алгоритм для участка 1--2: . (2)

4. Совместное решение (1) и (2) дает формулу (3).

;

; . (3)

5. Подставляя числовые значения, получим:

.

Ответ: ;

Задача 2. Четыре резистора сопротивлениями  Ом,  Ом,  Ом,  Ом, а также источник с  В и внутренним сопротивлением  Ом соединены по схеме, указанной на рис.22. Найти силу тока в цепи.

Дано: Решение

 Ом, а) б)

 Ом,

 Ом,

 Ом,

 В

 Ом

I - ?

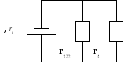
в) г)

Рис.22

В схеме (а) резисторы и соединены параллельно (рис.22б), затем к ним последовательно включен резистор (рис.22в), и, наконец, ко всему этому участку включен резистор (рис.22г).

Тогда ;

;

, .

Общее внешнее сопротивление

; .

1. Ток в цепи находим по закону Ома для замкнутой цепи:

,

где - сопротивление внешней цепи,

- внутреннее сопротивление.

.

Ответ: .

Задача 3. Три гальванических элемента с электродвижущими силами , , и внутренним сопротивлением по 0,2 Ом каждый включены, как показано на рис.23, и замкнуты на внешнее сопротивление . Определить количество теплоты, выделяющееся ежесекундно во всей цепи.

Дано: Решение

Q-?

Рис.23

1. В схеме два узла А и В, где происходит разветвление токов.

2. Согласно алгоритмическому предписанию найдем полюса источников тока и дополним рисунок направлением напряженности поля сторонних сил и тока.

3. Применим закон Ома для неоднородного участка цепи А-С.

Участок А--В:

. (1)

Участок А--В:

. (2)

Участок A-R-C--B:

. (3)

4. Причем . (4)

Из (1), (2) и (3) найдем .

;

;

;

;

;

 (А);

 (А);

.

5. Найдем выделяющееся количество теплоты по закону Джоуля-Ленца.

;

Ответ: