Тема 10. Комплексные числа и многочлены.

Комплексным числом называется число вида , где ,-действительные числа, символ - мнимая единица, для которой . Число - называется действительной частью комплексного числа , число - мнимой частью. Комплексное число совпадает с действительным, а число называется чисто мнимым. Множество всех комплексных чисел обозначается .

Комплексное число изображается на плоскости с системой координат (называемой комплексной плоскостью) точкой, обозначаемой той же буквой и имеющей координаты . Действительные числа изображаются точками оси абсцисс, а чисто мнимые – оси ординат (поэтому ось называется действительной осью, а ось - мнимой осью). Комплексное число на комплексной плоскости изображается также радиус-вектором точки . Длина радиус-вектора называется модулем комплексного числа: , а угол его с осью называется аргументом комплексного числа: , . Аргумент комплексного числа вычисляют, как правило, по формуле: .

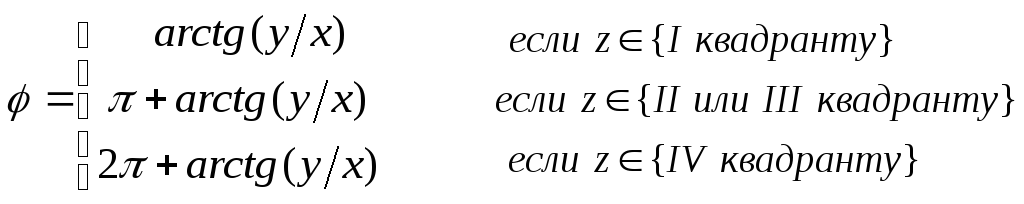Комплексно-сопряжённым числу называется число .

Представление комплексного числа выражением называется алгебраической формой комплексного числа, а выражением - тригонометрической формой комплексного числа.

Арифметические действия (сложение, вычитание, умножение) над комплексными числами в алгебраической форме выполняют по правилам действий над многочленами, с учётом того, что :

;

.

Деление комплексных чисел выполняют следующим образом: .

Возведение комплексного числа в натуральную степень выполняют, используя формулу Муавра: . Полученный результат представляют затем в алгебраической форме.

Извлечение корня -ой степени из комплексного числа (не равного нулю) выполняют по формуле:

,

(здесь - действительное положительное число). Таким образом, корень степени из комплексного числа имеет различных значений, расположенных на комплексной плоскости на окружности радиуса .

Алгебраическим многочленом степени называется выражение вида:

,

где , - некоторые числа (вообще говоря, комплексные), называемые коэффициентами многочлена, причём .

Алгебраическим уравнением степени называется уравнение вида Число , для которого называется корнем многочлена или уравнения.

Теорема Безу. Число является корнем многочлена тогда и только тогда, когда делится на , т.е. когда представляется в виде: , где - многочлен степени .

Число называется корнем кратности многочлена , если , где .

Для многочленов имеет место следующая теорема:

Теорема Гаусса (основная теорема алгебры). Всякий многочлен ненулевой степени имеет ровно корней, если каждый корень считать ровно столько раз, какова его кратность .

Всякий многочлен с действительными коэффициентами всегда можно разложить в произведение линейных и квадратичных множителей с действительными коэффициентами.

Всякий квадратный многочлен с действительными коэффициентами на множестве комплексных чисел всегда можно разложить в произведение линейных множителей: , где корни многочлена и находятся по формулам:

1) если , то - действительные;

2) если , то - комплексно-сопряжённые.

Для нахождения корней алгебраического уравнения с действительными коэффициентами поступают, как правило, следующим образом: находят один из корней подбором (например, корнем может быть целый делитель свободного слагаемого ), а затем, последовательно применяя теорему Безу, сводят нахождение корней уравнения к нахождению корней линейных и квадратных уравнений.