43. Теорема (о прямом произведении полуколец).

Прямое произведение полуколец является полукольцом.

Доказательство.

Пусть S₁- полукольцо подмножеств множества X₁,

S₂- полукольцо подмножеств множества X₂

Пусть - прямое произведение.

Докажем, что S является полукольцом подмножеств множества .

I. Пусть . Докажем, что .

Т.к. , то можем записать .

Аналогично , где , .

Имеем .

Т.к. S₁- полукольцо, то

Т.к. - полукольцо, то

Тогда .

II. Пусть , где , и , тогда

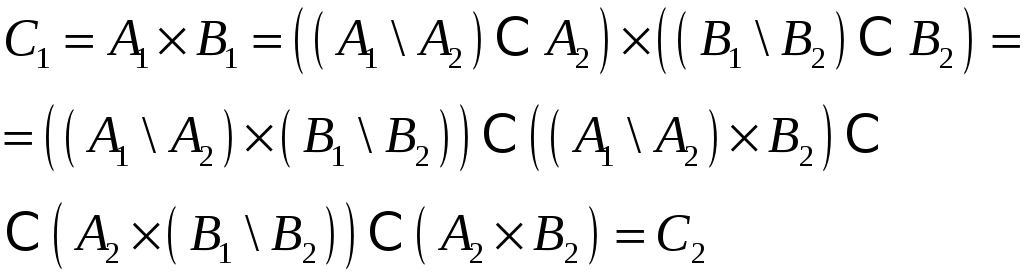
Получаем, что

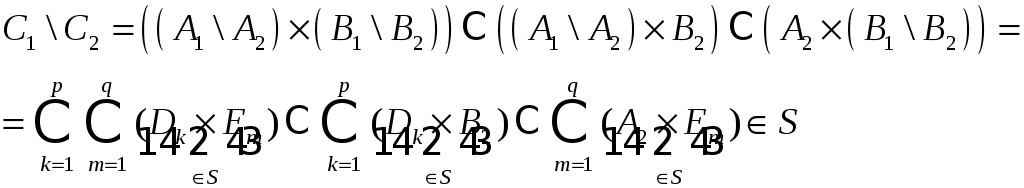В последних равенствах , 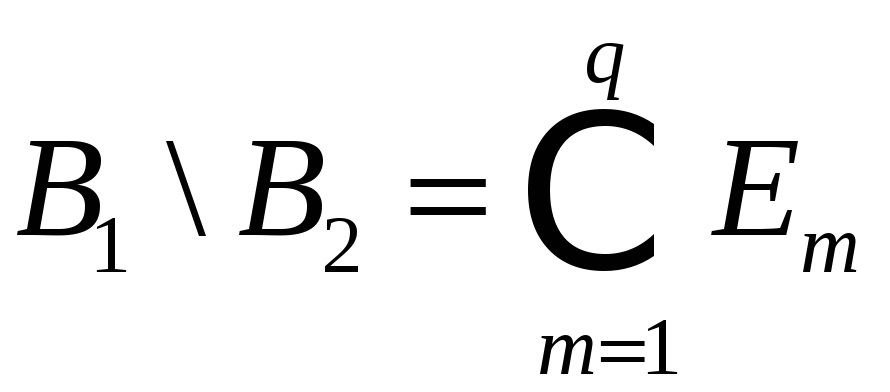т.к. .

Следовательно, S является полукольцом.

44. Тензорное произведение мер

Напомним, что если есть две функции f и g, то можно построить тензорное произведение этих функций:

.

Операция называется тензорным произведением.

Определим векторное произведение :

.Аналогично для

В пр-ве X₁ рассмотрим пулокольцо мн-в S₁, а в пр-ве X₂ –S₂.

Определим - прямое произведение полуколец S₁ и S₂.