18.Внешняя мера и ее св-ва

Пусть есть мн-во AK, К—алгебра.

Определение. Счетным покрытием множества называется семейство непересекающихся мн-в таких, что .

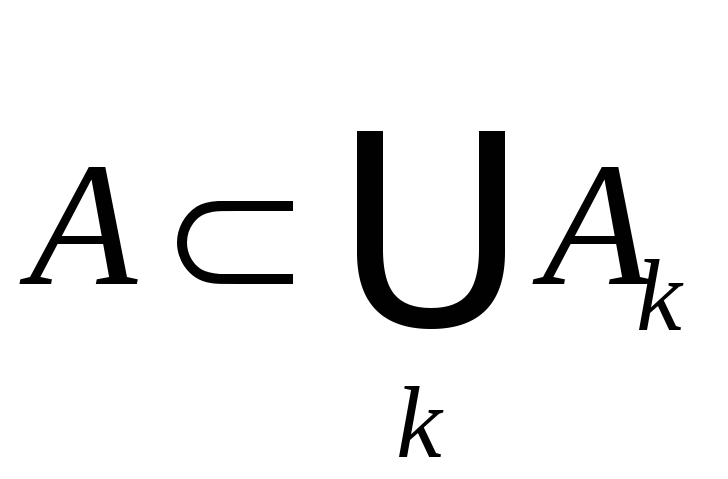Пример.

Пусть , тогда .

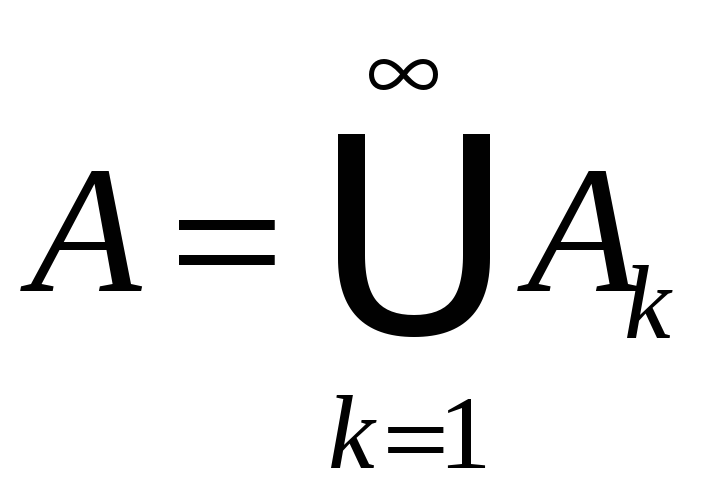Определение. Пусть – произвольное множество, и пусть – алгебра, т.е., на которой задана аддитивная мера . Тогда внешней мерой множества называется число

.

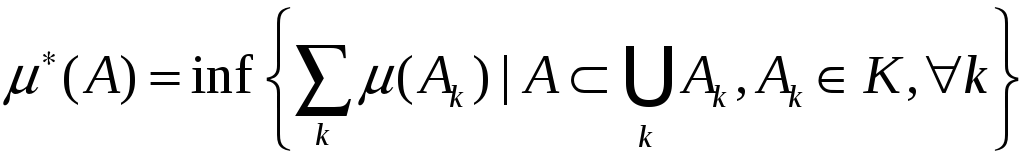Отображение называется внешней мерой.

Определение. Множество называется измеримым, если для

- множество измеримых множеств. Отметим, что явл. метрикой , т.е.

Любое множество из является измеримым, т.е. если , то оно измеримо.

Доказательство.

Мера наз-ся внешней мерой Лебега на и обозначается .

Упорядоченная тройка (Х, ,) наз-ся пространством с мерой.

Если (Х)=1, то пр-во с мерой наз-ся вероятностным пр-вом. Эл-ты Х –элементарные события, Эл-ты -события.

19.

20.

21.

22.

23.

24.

25.

26.