§ 37. Способы приближений решения нормальных уравнении

При решении большого числа нормальных уравнений часто применяют не прямые способы, к которым принадлежат рассмотренные ранее способы Гаусса и квадратных корней, а так называемые способы приближений. Если в прямых способах решение получают путем выполнения конечного, заранее известного числа арифметических операций, то способы приближений основаны на постепенном уточнении неизвестных, выполняемом до тех пор, пока максимальная разность ( будет меньше наперед заданного положительного числа ε, определяемого необходимой точностью вычислений. Число приближений ρ при этом заранее указать невозможно. Вычисление неизвестных в каждом m-м приближении требует значительно меньшего объема вычислений, чем получение неизвестных в прямых методах. Эффективность способов итераций, следовательно, целиком определяется количеством приближений, которое зависит от скорости сходимости процесса. Объем вычислений в прямых методах возрастает примерно пропорционально кубу числа уравнений, поэтому способы итераций для решения больших систем уравнений часто оказываются более эффективными.

Прежде чем начать вычисления, систему уравнений Ах = b необходимо привести к виду, удобному для итераций,

(3.84)

Пусть дана система нормальных уравнений

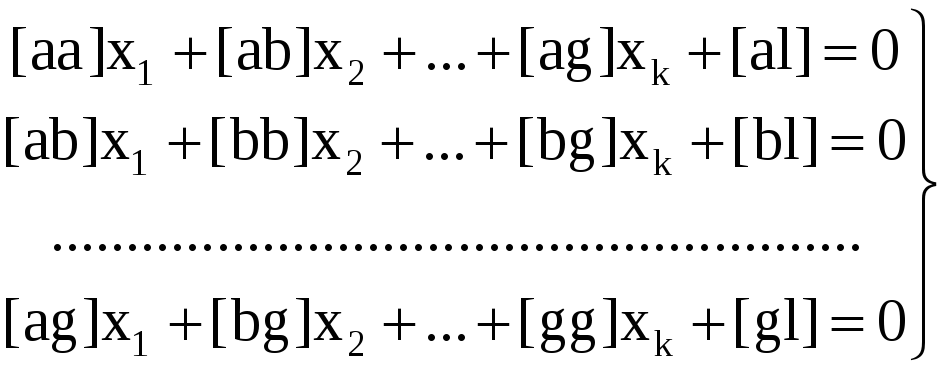
Так как диагональные коэффициенты все не равны нулю, то каждое j-е уравнение можно разрешить относительно х_j следующим образом·

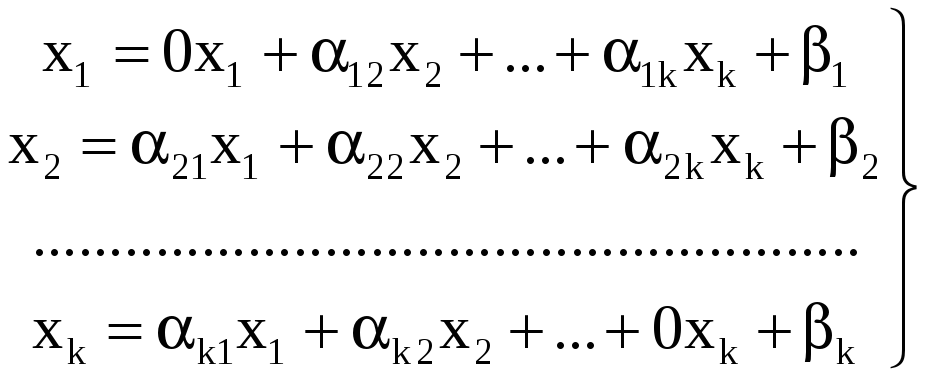(3.85)

где вектор

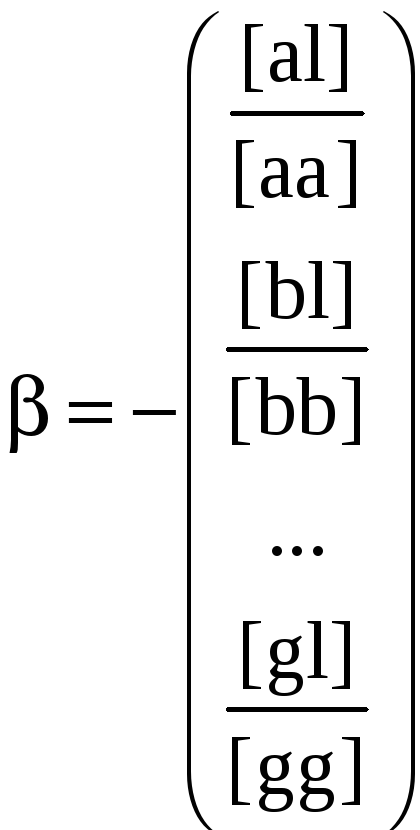
а матрица

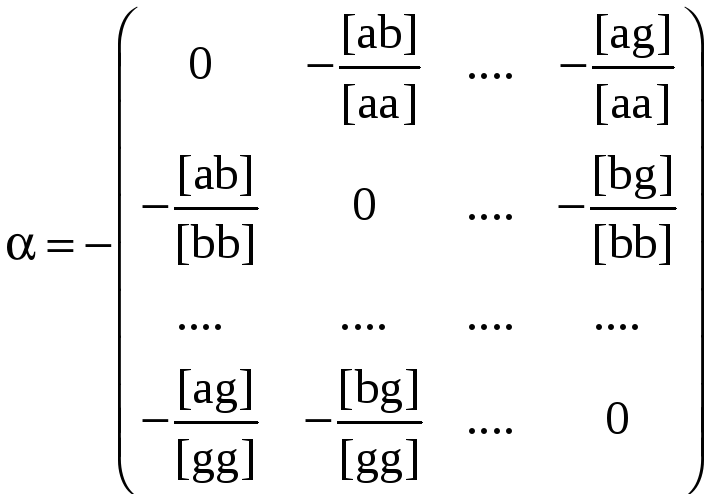
Уравнение (3.84) и представляет матричную запись уравнений (3.85). Далее последовательно находим векторы (первое приближение), (второе приближение) и т. д.

Любое m приближение вычисляют по формуле

В качестве нулевого приближения можно принять вектор свободных членов, т. е.

В подробной записи формулы приближений имеют вид

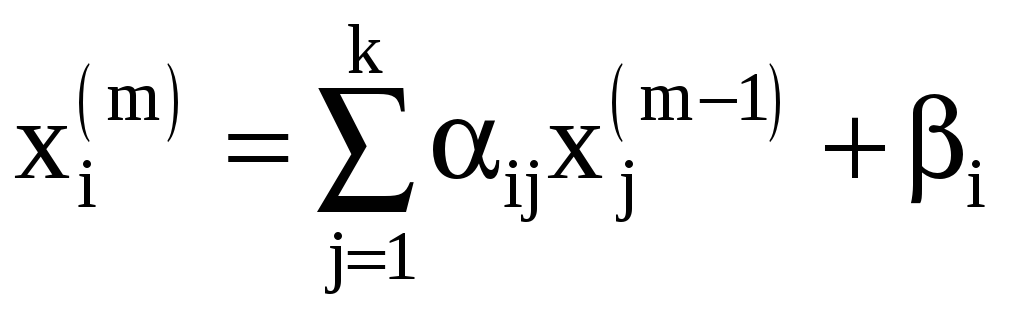
Рассмотренный метод последовательных приближений носит название метода простой итерации. Он быстро сходится, если элементы матрицы α малы по абсолютной величине. Достаточные условия схо­димости процесса следующие:

1)

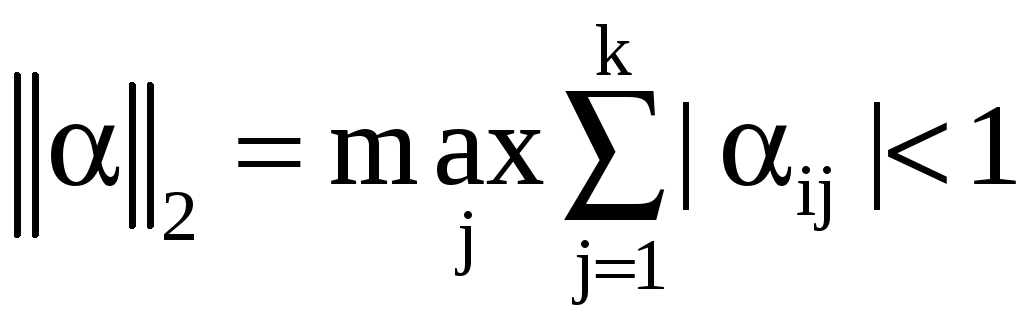
или 2)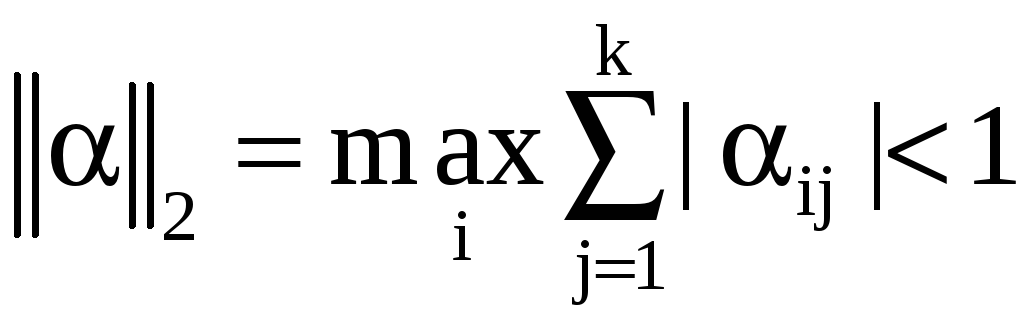

или 3)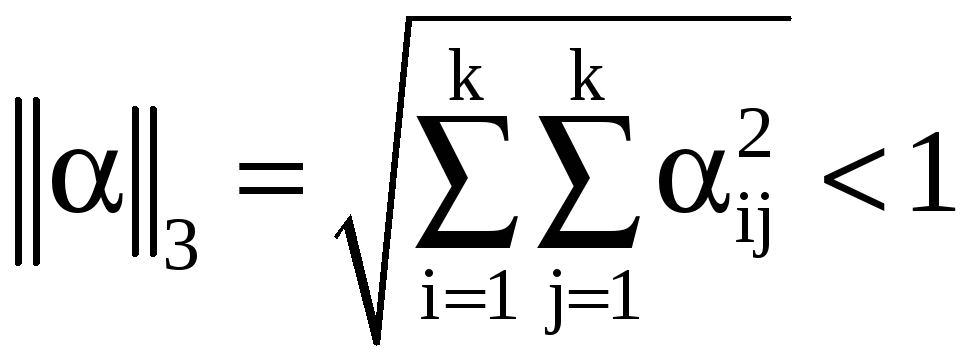

Величины ||а||₁ ||α||₂, называемые соответственно первой и второй нормой матрицы а, представляют максимальную сумму модулей элементов матрицы а по строкам или столбцам. Третья норма ||а||₃ есть сумма квадратов всех ее элементов. Можно также доказать, что сходимость имеет место, если диагональные элементы матрицы А системы превышают сумму модулей недиагональных элементов для каждой строки или для каждого столбца. В качестве примера решим систему нормальных уравнений

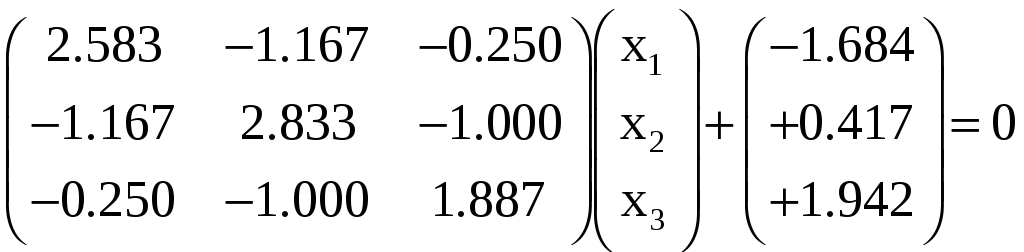(3.86)

Легко проверить, что процесс будет сходиться, так как 2,583 > 1,417; 2,833 > 2,167; 1,887 > 1,250.

Вычисления располагаем в табл. 95.

Τаблица 95
0 0,412 0,132	0,452 0 0,530	0,097 0,353 0	0,652 -0,147 -0,029	0,5 -0,2 - 1,0	0,46 -0,29 -1,12	0,41 -0,38 -1,18

Продолжение табл. 95
0,37 -0,39 -1,19	0,36 -0,41 -1,20	0,35 -0,42 - 1,20	0,34 -0,43 - 1,21	0,340 -0,434 - 1,212	0,338 -0,435 - 1,215	0,338 -0,437 -1,215	0,337 -0,437 -1,216

Так как max = 0,001, то вычисления заканчиваем. Значения неизвестных получились такими же, как и при решении нормальных уравнений по схеме Гаусса или методу квадратных корней (см. примеры в § 29, 36).

Отметим, что так как окончательный результат не зависит от начального приближения, то точность вычислений целесообразно увеличивать по мере улучшения сходимости.

Видоизменением метода простой итерации является метод Зейделя, который для системы нормальных уравнений всегда сходится. Отличием этого метода является то, что при вычислении используются значения (l=1,2, ..., j-1) уже полученные в этом же приближении. Формулы для вычислений имеют вид

…………………………………..

……………………………………

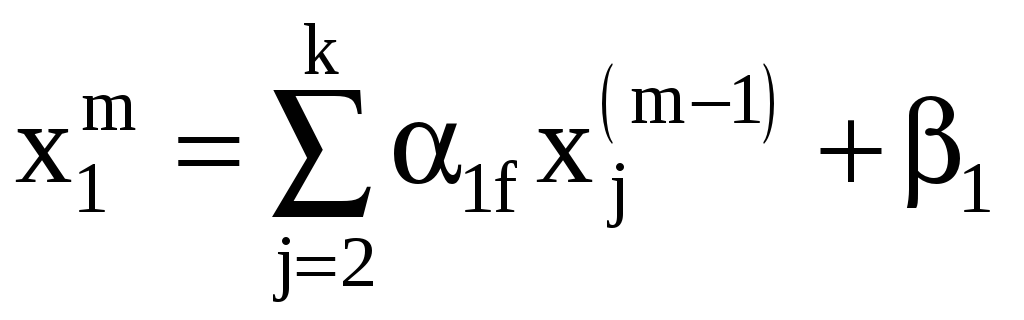
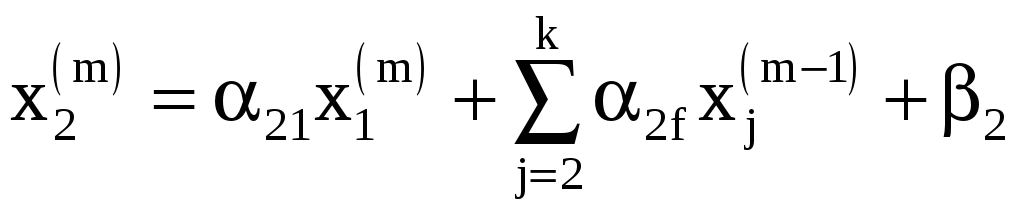
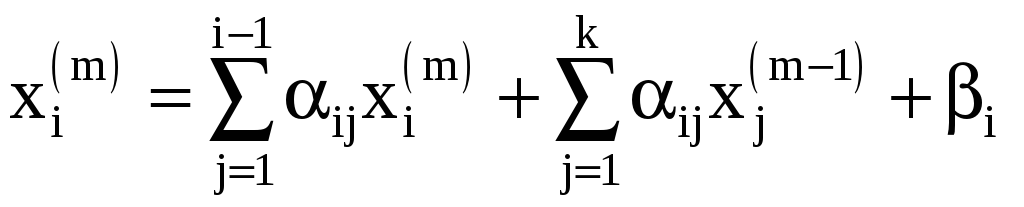
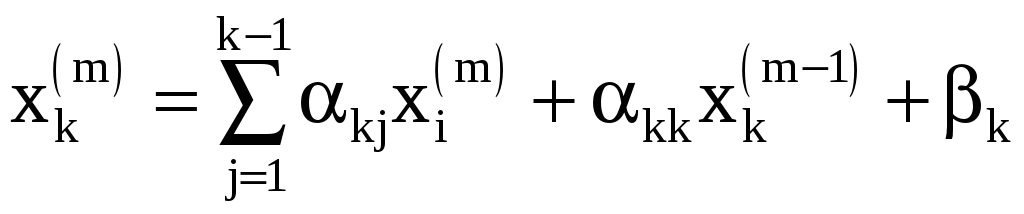
Например, для k = 3

В табл. 96 приведено решение системы (3.86) по методу Зейделя.

Таблица 96
0 0,412 0,132	0,452 0 0,530	0,097 0,353 0	0,652 -0,147 -1,029	0,5 -0,3 - 1,1	0,41 -0,31 -1,14

Продолжение табл. 96
0,40 -0,38 -1,18	0,37 -0,41 -1,20	0,35 -0,43 -1,21	0,340 -0,434 - 1,214	0,338 -0,436 -1,215	0,337 -0,437 -1,216

Обычно метод Зейделя дает лучшую сходимость, чем метод простои итерации, хотя это бывает не всегда.

Отметим, что в геодезии для уравнивания геодезических сетей часто применяют методы приближений, располагая вычисления на схеме сети и полагая последовательно все пункты, за исключением одного, исходными. Нетрудно показать, что по существу это тоже есть метод Зейделя, только оформленный в иной вычислительной схеме. Представляется, однако, что рассмотренная здесь схема более удобна и поэтому упомянутые способы применять нецелесообразно.

Легко понять, что для получения обратной матрицы Q, необходимой для оценки точности в параметрическом способе, также можно применить метод простой итерации или Зейделя, приняв столбцы свободных членов равными –Еj, как и в методе Гаусса (см. § 30).

3.61. Методом простой итерации и Зейделя найти с точностью до 0,01 последний столбец матрицы Q для системы нормальных уравнений (3.86)

3.62. Можно ли применить для решения системы нормальных уравнений

составленной в задаче 3.17, метод простои итерации?

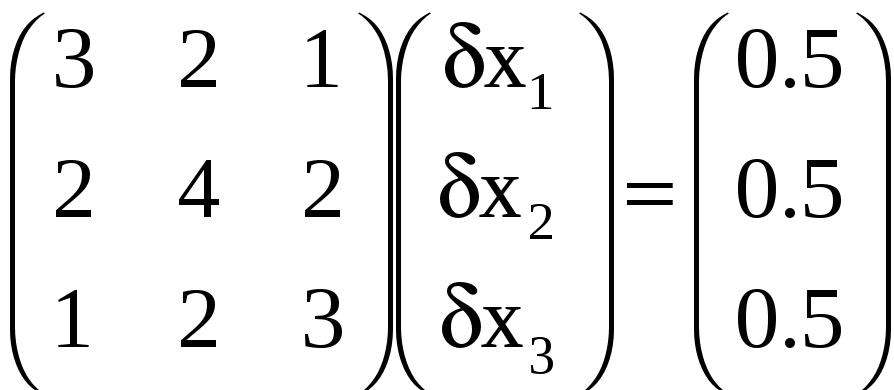(3.87)

3.63. Решить систему (3.87) по методу Зейделя. Получить также матрицу Q=R^1-

3.64 Решить по методу итераций и Зейделя одну из систем нормальных уравнений из задачи 3.18.

3.65.В угломерном ходе с n поворотными точками составить в общем виде уравнения поправок и матрицу коэффициентов нормальных уравнений, приняв в качестве неизвестных поправки дирекционных углов сторон. Можно ли полу­ченную систему решать по способу простой итерации? Найти по этому методу первую, вторую и третью строки обратной матрицы. Обнаружив простую закономерность в образовании этих строк, написать всю обратную матрицу.