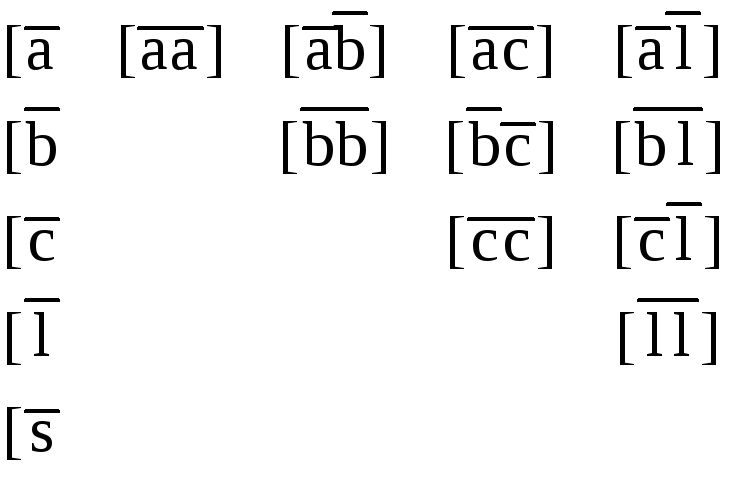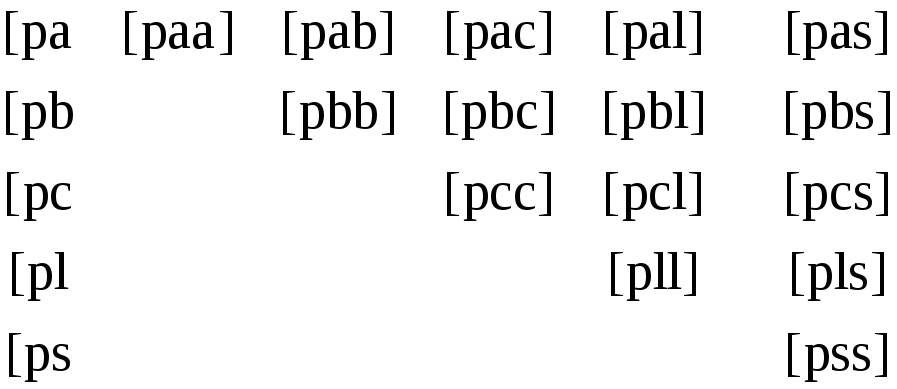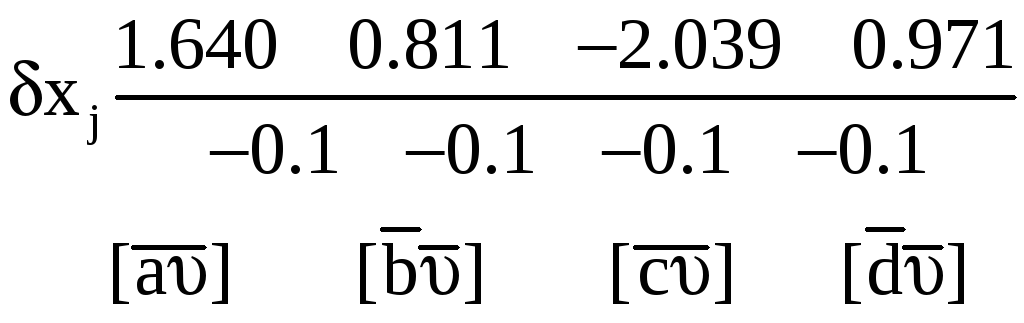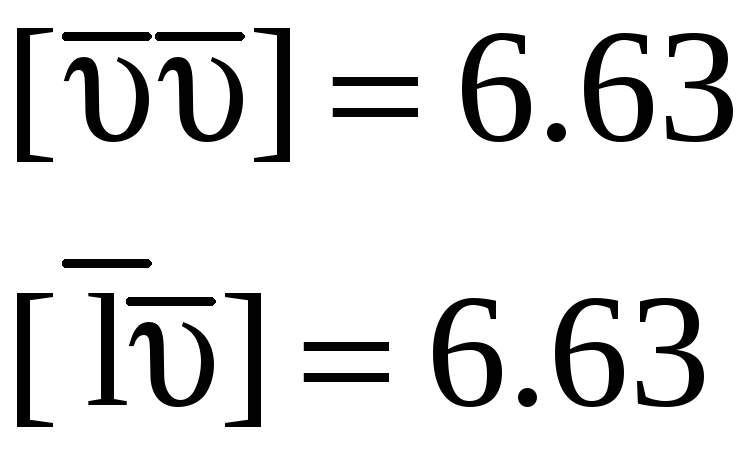§34. Уравнивание неравноточных измерений параметрическим способом

Уравнивание неравноточных измерений выполняется под условием [ρυυ]= V^TPV = min, где p_i - веса измерений, а Р - диагональная матрица,

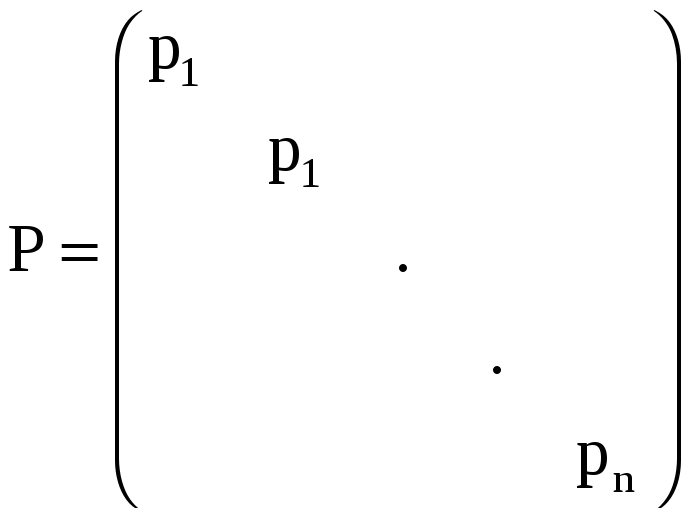
Вопрос установления весов p_i был нами рассмотрен в § 24. Исходная система связи и уравнения поправок составляются так же, как и в случае равноточных измерений, но в отличие от него система нормальных уравнений имеет вид

(3.71)

где алгоритмы

…………………………………….

………………………………….

В матричной форме уравнения (3.71) можно записать в виде

(3.72)

где

(3.73)

(3.74)

Процесс вычислений при уравнивании неравноточных измерений, следовательно, отличается от уже рассмотренного случая лишь схемой составления нормальных уравнений. При этом можно поступить двояко: 1) привести неравноточные измерения к равноточным путем умножения i-го уравнения поправок на величину 2) нормальные уравнения составлять непосредственно по формулам (3.13) и (3.14).

В первой схеме (А) будем иметь систему уравнений поправок

…………………………………..

Где

и систему нормальных уравнений

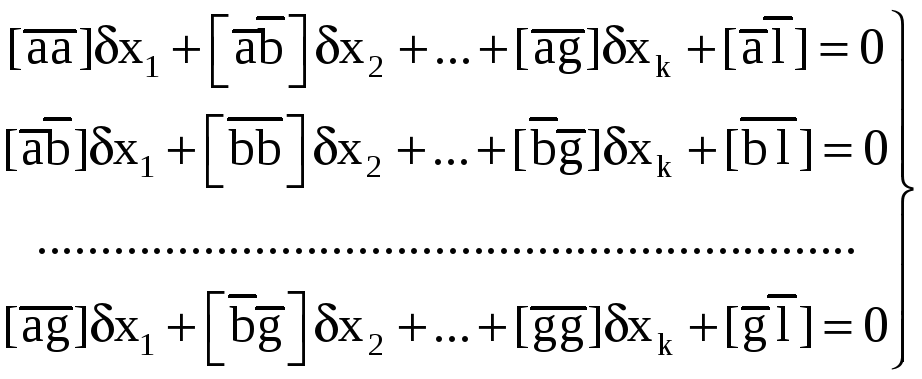
совпадающую с (3.72). Ясно, также, что [ρυυ] = []. Схема составления системы нормальных уравнений будет состоять из следующих двух таблиц (табл. 80, 81). Для простоты принято k = 3.

Во второй схеме (В), которую применяют чаще, приходится составлять следующие таблицы (табл. 82 и 83).

Таблица 80
Номера измерении	ai bi ci li	si
1 2	a1 b1 c1 l1 a2 b2 c2 l2 ………… an bn cn ln	s1 s2 … s3	…	……..	…	…

Таблица 81
		Контроль

Таблица 83
	Контроль

Таблица 82
Номера измерений	ai bi ci li	si	pi	ai pi bi pi ci pi li pi	sipi	υi
1 2 … n	a1 b1 c1 l1 a2 b2 c2 l2 …………….. an bn cn ln	s1 s2 … sn	p1 p2 …. pn	a1 p1 b1 p1 c1 p1 l1 p1 a2 p2 b2 p2 c2 p2 l2 p2 ………………………………….. an pn bn pn cn pn ln pn	s1p1 snp2 … snpn	υ1 υ2 … υn

Решение нормальных уравнений, оценка точности неизвестных и их функций выполняется точно так же, как и в случае равноточных измерений. Следует лишь иметь в виду, что во всех формулах, относящихся к этому процессу, в алгоритмах Гаусса с двумя буквами добавляется буква р.

3.48. Уравнять параметрическим способом нивелирную сеть, представленную на рис. 56 (исходные данные приведены ниже), а результаты измерений - в табл. 84.

Таблица 84
Номера ходов	Превышение hi, м	Длина хода Li, км
1	+6,135	33,0	1,21
2	+8,343	33,9	1,17
3	+5,614	30,4	1,31
4	+ 1,394	32,7	1,22
5	-6,969	31,8	1,25
6	-0,930	29,9	1,34
7	+6,078	34,5	1,15

Марки Высоты исходных

марок, м

А 183,506

В 192,353

С 191,880

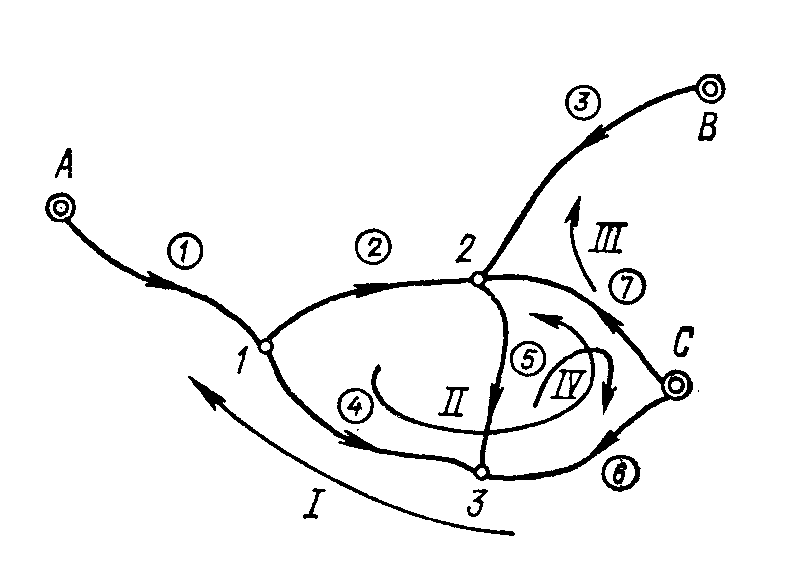
Рис. 56

Решение. Приближенные значения высот реперов получаем так:

Составляем уравнения поправок:

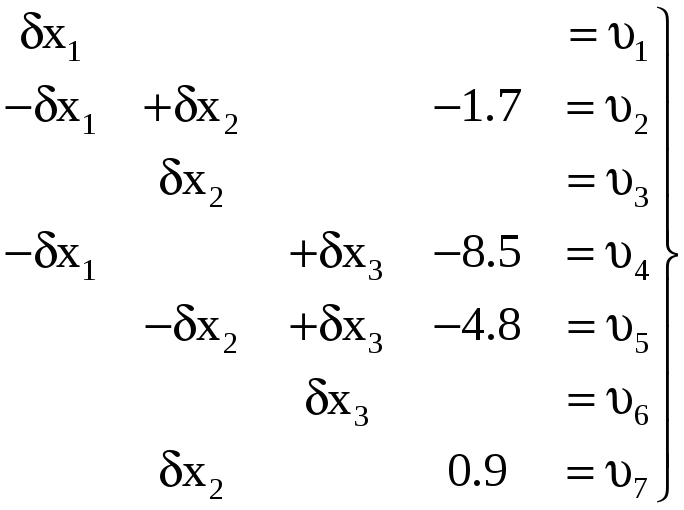
Таблица 85
Номера уравнений
1	+ 1	0	0	0,0	+ 1,0	1,21	-2,64
2	- 1	+ 1	0	- 1,7	- 1,7	1,17	+0,08
3	0	+ 1	0	0,0	+ 1,0	1,31	-0,85
4	-1 -	0	+ 1	-8,5	-8,5	1,22	-2,69
5	0	- 1	+ 1	-4,8	-4,8	1,25	-0,77
6	0	0	+ 1	0,0	+ 1,0	1,34	+3,17
7	0	+ 1	0	+0,9	+ 1,9	1,15	+0,05
	- 1	+2	+3	-14,1	- 10,1
δxj Контроль	-2,64 0,00	-0,85 0,01	+3,17 -0,01		[ρυυ] = 32,42

Таблица 86
a]	b]	с]	l]	s]	Контроль	F1	F2	Σ	SQ
[pa +3,60 [pb [pc [pl [ps	- 1,17 +4,88	-1,22 -1,25 +3,81	+12,36 +5,05 -16,37 + 121,9	+ 13,57 +7,51 -15,03 + 122,30 +128,35	+ 13,57 7,51 - 15,03 122,30 128,35	+ 1,00 0 0	00 1,00 -1,00	+2,21 +3,46 +0,34 1,00 0	12,97 6,61 -16,03
Σ1=[as]-[al]+(f1)1+(f1)2 Σ2=[bs]-[bl]+(f2)1+(f2)2 Σ3=[cs]-[cl]+(f3)1+(f3)2

Свободные члены выражены в сантиметрах.

Веса измерений вычисляем по формуле p_i= 40/L_i.

В табл. 85 и 86 приведены коэффициенты уравнений поправок и нормальных уравнений.

В качестве оцениваемых функций выбраны превышения по ходам 1 и 5. Для первой функции F₁ коэффициенты f₁ = 1, f₂ = 0, f₃ = 0, для второй f₁ = 0, f₂ = 1, f₃ = - 1. В столбце Σ табл. 86 два последних числа равны соответственно [f]₁ = 1 и [f]₂ = 0.

Решение системы нормальных уравнении приведено в табл. 87.

В результате проведенного решения получены следующие значения неизвестных:

X₁ = 189,641 м - 2,64 см = 189,615 м;

Х₂= 197,967 м - 0,85 см = 197,953 м;

х₃= 190,950 м + 3,17 см = 190,981 м.

Средние квадратические ошибки единицы веса и на 1 км хода равны:

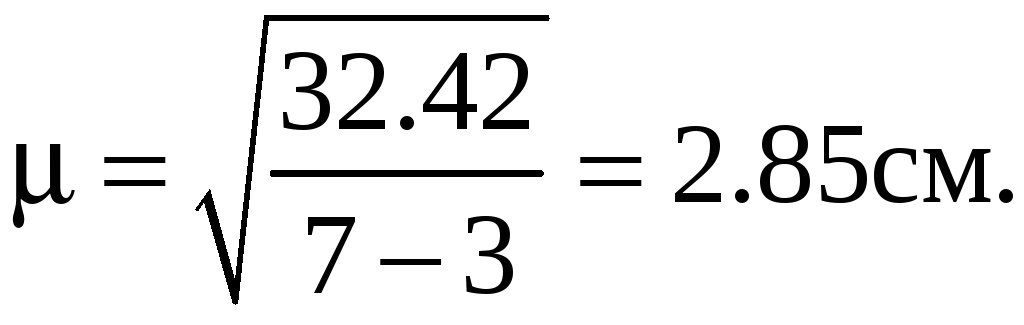
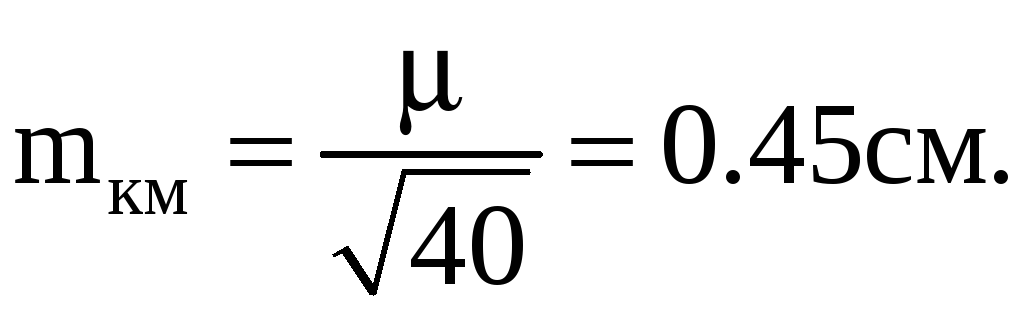
Вес последнего неизвестного равен

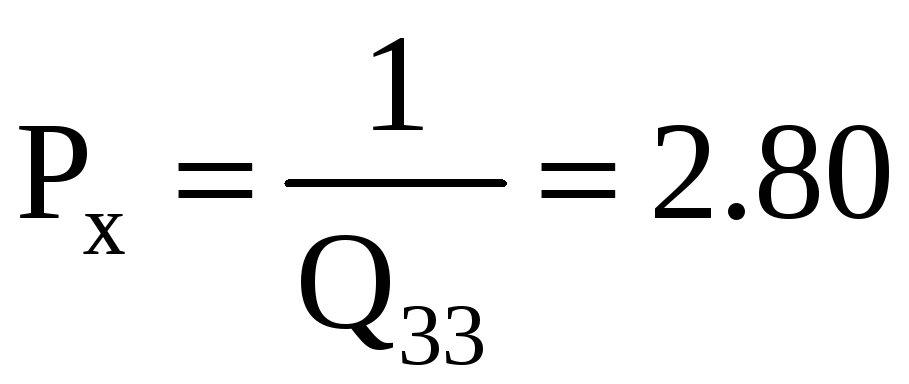
Вес первого неизвестного получен дважды

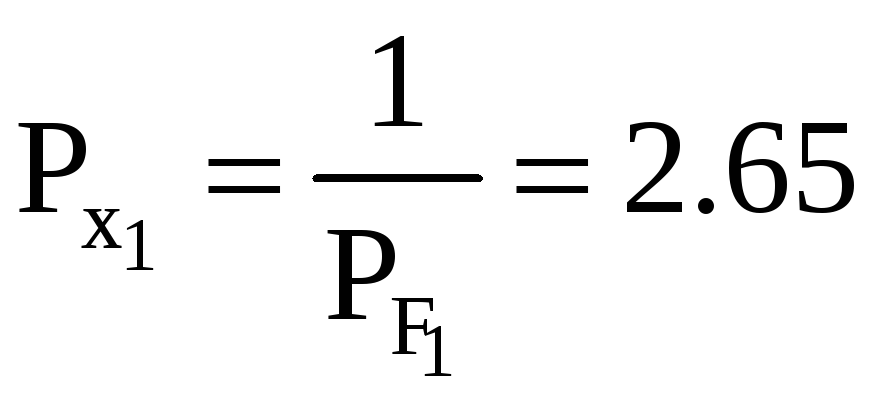
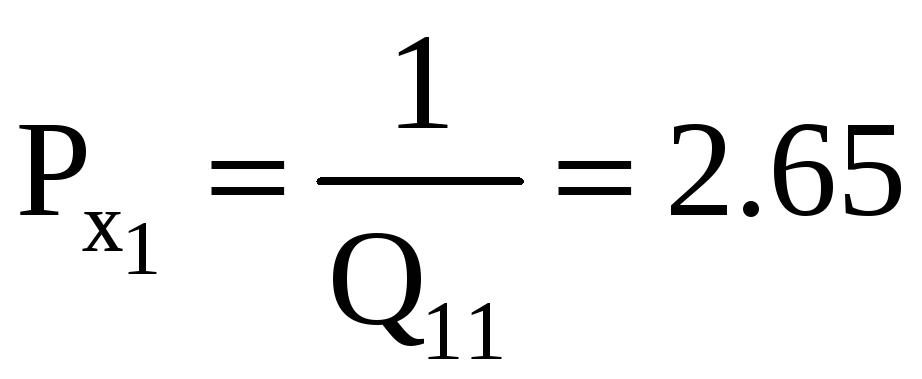
Вес предпоследнего неизвестного

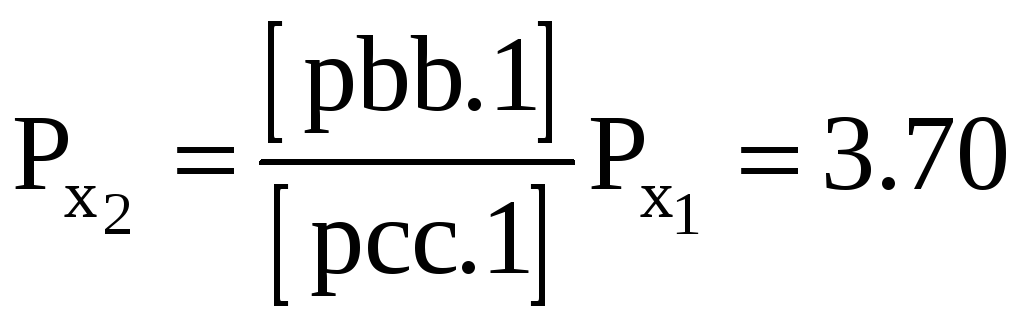
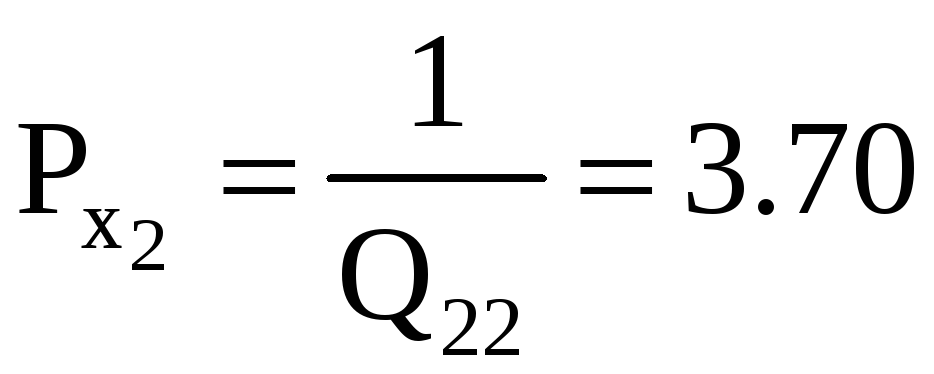
Средние квадратические ошибки:

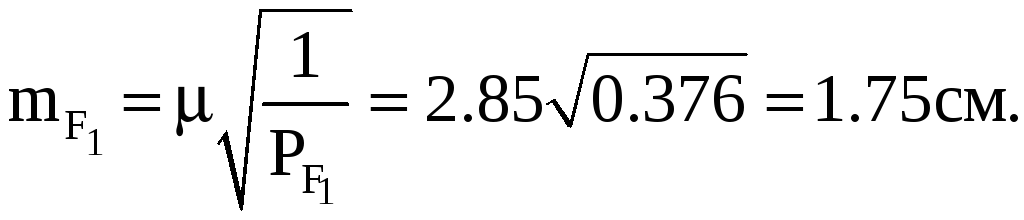
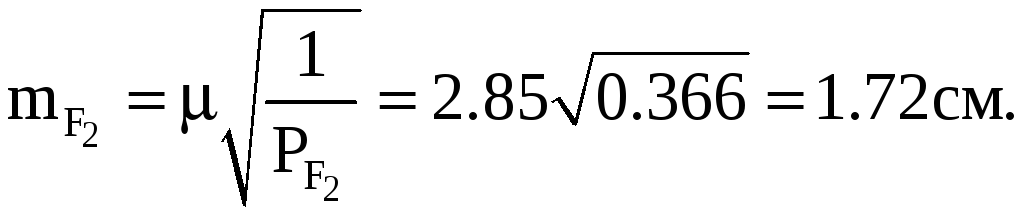
После введения поправок в измеренные величины получим

Таблица 87

δx1

δx2

δx3

l

S

Контроль 1

Q1

Q2

Q3

Qs

Контроль 2

F1

F2

Σ

Контроль 3

+3,60 (0,2778) (-1)

- 1,17 +0,325

-1,22 +0,339

+ 12,36 -3,433

+ 13,57 -3,769

+ 13,57 -3,769

- 1,00 +0,278

0 0

0 0

+12,57 -3,492

12,57 -3,491

+ 1,00 -0,278

0 0

+2,21 -0,614

+2,21 -0,614

(0,2222)

4,50 (-1)

-1,65 +0,366

+9,071 +2,015

11,92 -2,649

+ 11,92 -2,649

-0,32 +0,072

- 1,00 +0,222

0 0

+ 10,60 -2,355

+ 10,60 -2,355

+0,32 -0,072

+ 1,00 -0,222

+4,18 -0,929

+4,17 -0,928

(0,3571)

+2,80

-8,86 +3,171

-6,07 +2,172

-6,06 +2,171

-0,46 +0,164

-0,37 +0,131

- 1,06 +0,357

-7,89 +2,818

-7,90 +2,823

+0,46 -0,164

-0,63 +0,227

+2,62 -0,936

+2,63 -0,937

32,44

32,44 32,44

+0,031 -0,366

-0,345 -0,333

-0,345 -0,335

δx1

δx2

δx3

-2,636 -3,638

-0,855 - 1,855

+3,171 +2,171

+ 1,002

1,000

1,000

Весовые коэффициенты

+0,376 +0,132 +0,164

+0,132 +0,270 +0,131

+0,164 +0,131 +0,358

Окончательным контролем правильности решения задачи является выполнение равенства для каждого хода сети.

Способ узлов проф. В. В. Попова для составления нормальных уравнений

Для случая уравнивания нивелирных сетей и углов в сети полигонометрии проф. В. В. Попов предложил следующие правила составления нормальных уравнений с помощью чертежа сети:

а) квадратичные коэффициенты нормальных уравнений в строке j равны сумме весов ходов, сходящихся в узле с тем же номером j;

б) неквадратичные коэффициенты, расположенные в строке i и столбце h, равны отрицательному весу хода, соединяющего узлы с номерами j и h;

в) свободные члены нормальных уравнений получаются суммированием величин ±P_il_i тех ходов, которые сходятся в узле j, причем если узел является конечной точкой хода, то ставится знак «+», а если начальной, то «-».

Например, для нивелирной сети (см. рис. 56) нормальные уравнения будут

а свободные члены

Указанные правила тождественны следующим формулам составления матрицы R системы нормальных уравнений (3.72) ее диагональные элементы

(3.75)

(запись ij означает здесь принадлежность i-го хода j-му узлу), а недиагональные

(3.76)

(знак суммы предусматривает случай, когда узлы j и k соединены несколькими ходами).

Вектор свободных членов b имеет элементы

(3.77)

3.49. Составить по способу В. В. Попова систему нормальных уравнений в задаче 3.48.

3.50. Выполнить параметрическим способом уравнивание сети триангуляции (рис. 57), если . в ней измерены дирекционные углы

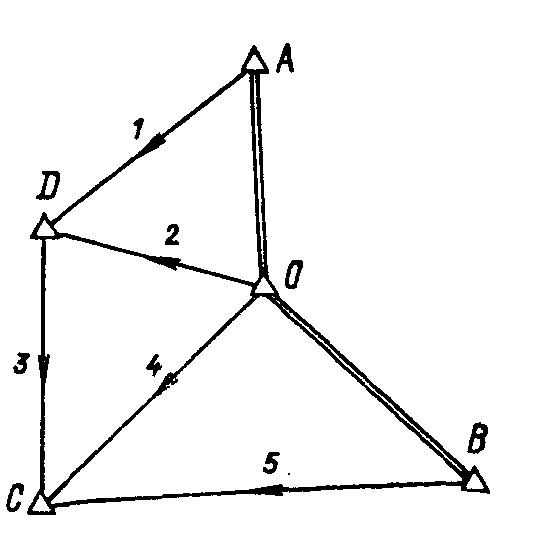
Рис. 57

Номера дирекционных Измеренные значения

углов

1 229°30'17,9'

2 294 06 17.4

3 183 34 12,7

4 238 54 00,7

5 281 56 01,2,

матрица весов которых

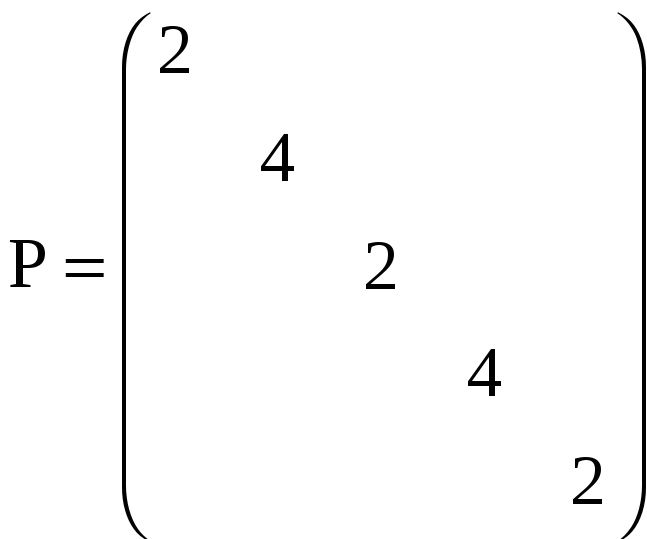
Координаты исходных пунктов взять из задачи 3.36. Исходные дирекционные углы

α_OA =0°; α_OB = 135°40’19,5".

Приближенные значения координат определяемых пунктов примем равными приведенным ниже:

Пункт Ρ x⁽⁰⁾ y⁽⁰⁾

D 623,360 - 1393,272

С - 897,701 - 1488,183

Решение. Эта задача отличается от решенной ранее задачи 3.37 лишь тем, что теперь дирекционные углы неравноточны**. Таблицы коэффициентов уравнений поправок и составления нормальных уравнений имеют вид, приведенный в табл. 88, 89.

Решение нормальных уравнений и получение матрицы весовых коэффициентов представлено в табл. 90, а вычисление поправок , с контролем и - в табл. 88.

Уравненные значения координат и уравненных дирекционных углов приведены ниже.

Пункт F х(р) у(0)

D 623,376 -1393,264

С -897,721 1488,173

Номера дирекционных углов Уравненные дирекционные

1 229°30'18,6"

2 294 06 17,2

3 183 34 13,3

4 238 54 00,2

5 281 56 02,6

При уравнивании этого построения имеем всего одно избыточное измерение, поэтому вычислить ошибку единицы веса μ не представляется возможным. Однако учитывая, что в качестве измеренных углов здесь приняты предварительно уравненные углы из задачи 3.36, можно применить формулу

где через - обозначены поправки углов, уравненных в задаче 3.36.

Таблица 88
ai	bi	ci	di		li	si								Контроль
0,858	-0,731	0	0		-0,1	0,027	1,414	1,213	-1,034	0	0	-0,141	0,038	0,038	1,01	0,71
1,234	0,552	0	0		-2,7	-0,914	2,000	2,468	1,104	0	0	-5,400	-a, 828	-1,828	-0,46	-0,23
-0,084	1,350	0,084	- 1,350		1,1	1,100	1,414	-0,119	1,909	0,119	-1,909	1,556	1..556	1,556	0,81	0,57
		1,018	-0,614		2,2	2,604	2,000			2,038	-1,228	4,400	5,208	5,210	-0,95	-0,48
		0,662	0,140		2,6	3,402	1,414			0,936	0,198	3,676	4,810	4,808	1,96	1,39
				Коэффициенты увеличены в 10 раз

Таблица 89
							Контроль
	7,577	1,243	-0,014	0,227	- 13,683	-4,650	-4,650
		5,932	0,227	-3,644		0,913	0,913
			5,043	-2,544	12,593	15,301	15,305
				5,191	-7,646	-8,414	-8,416
					64,474	52,884	52,893
						56,024	56,034

Таблица 90
Вспомогательные величины					l	s	Контроль
(0,1320)	7,577 (-1)	1,243 -0,1640	-0,014 0,0018	0,227 -0,0300	-13,683 1,8056	-4,650 0,6137	-4,650 0,6134
	(0,1746)	5,728 -1	■0,229 -0,0400	-3,681 0,6426	-0,601 0,1049	1,676 -0,2926	1,675 -0,2925
		(0,1986)	5,034 -1	-2,296 0,4760	12,592 -2,5014	15,230 -3,0254	15,230 -3,0254
			(0,5965)	1,678 (-1)	-1,628 0,9713	0,048 -0,0286	0,048 -0,0287
	1,6398 0,6401	0,8106 -0,1894	-2,0391 -3,0390	0,9713 -0,0286	6,626	6,623 6,611
	0,9997	1,0000	0,9999	0,9999	10-4
1,000 1,000 0,999 1,001	0,1470 - 0,0776 -0,0356 -0,0784	-0,0776 0,4069 0,1691 0,3720	-0,0356 0,1691 0,3337 0,2839	-0,0784 0,3720 0,2839 0,5965

Тогда

Оценка точности уравненных координат выполняется по формулам

а их функций - точно так же, как и в задачах 3.36-3.38, а именно:

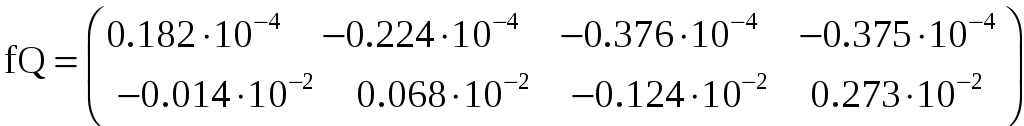
Поэтому

3.J51. Для условий задачи 3.50 составить нормальные уравнения, пользуясь схемой А (не приводя измерения к равноточным). Сделать выводы о преимуществе схемы А или В с точки зрения объема и точности вычислений.

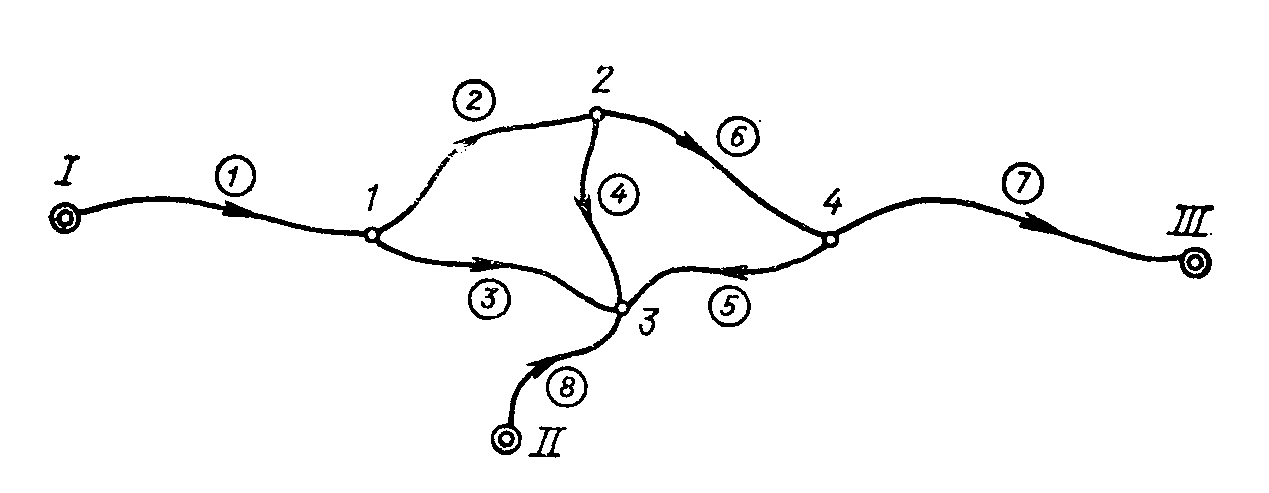
Рис. 58

3.52. Выполнить уравнивание нивелирной сети, изображенной на рис. 58. Оценить точность всех узловых реперов (матрицу весовых коэффициентов

получить по способу Ганзена) и уравненного превышения h_i. Обратный вес этой функции вычислить по формуле (3.49) и в дополнительном столбце схемы Гаусса. Исходные данные приведены ниже, а измеренные превышения и длины ходов даны в табл. 91. Нормальные уравнения составить дважды: по схеме В и по способу узлов проф. В. В. Попова.

Номера опорных реперов Высоты опорных реперов, м

I 188,452

II 188,838

III 186,298

3.53. Выполнить предварительное уравнивание углов в полигонометрической сети (рис. 59). Оценить точность дирекционных углов узловых направлений, совпадающих со сторонами 1-30 и 2232. Суммы измеренных левых углов в ходах и исходные дирекционные углы на рис. 59 [3].

Решение. Суммы измеренных углов в каждом ходе принимаем в качестве измеренных величин (как и превышения ходов в нивелирной сети). Веса ходов принимаем равными , где - число измеренных углов в каждом ходе. Предполагается, что на узловых точках углы измерены отдельно друг от друга. Далее вычисляем приближенные значения дирекционных углов сторон 1-30 и 2-32 по ходам 1 и 3:

= 196°08'42,3', = 162°38'47,1".

Таблица 91
	Превышения, м	Длина хода, км
		Варианты
		1	2	3	4	5	6	7	8	9	10
1	+2,214+0,001i	12,8	13,4	14,0	8,0	11,1	11,8	13,2	15,1	16,6	17,5
2	+1,566	14,2	14,8	15,5	8,9	12,3	13,1	14,6	16,7	18,3	19,4
3	-0,302	8,7	9,1	9,5	5,4	7,6	8,0	8,9	10,2	11,2	11,8
4	-1,881	12,4	13,0	13,6	7,7	10,7	10,4	12,8	14,6	16,0	16,9
5	+0,915	5,8	6,1	6,4	3,6	5,1	5,4	6,0	6,9	7,5	7,9
6	-2,814	5,1	5,3	5,6	3,2	4,4	4,8	5,2	6,0	6,5	6,9
7	-3,137	7,8	8,3	8,6	4,9	6,8	7,2	8,1	9,2	10,1	10s6
8	+ 1,517+0,001i	10,1	10,7	11,1	6,3	8,8	9,4	10,4	12,0	13,1	13,8

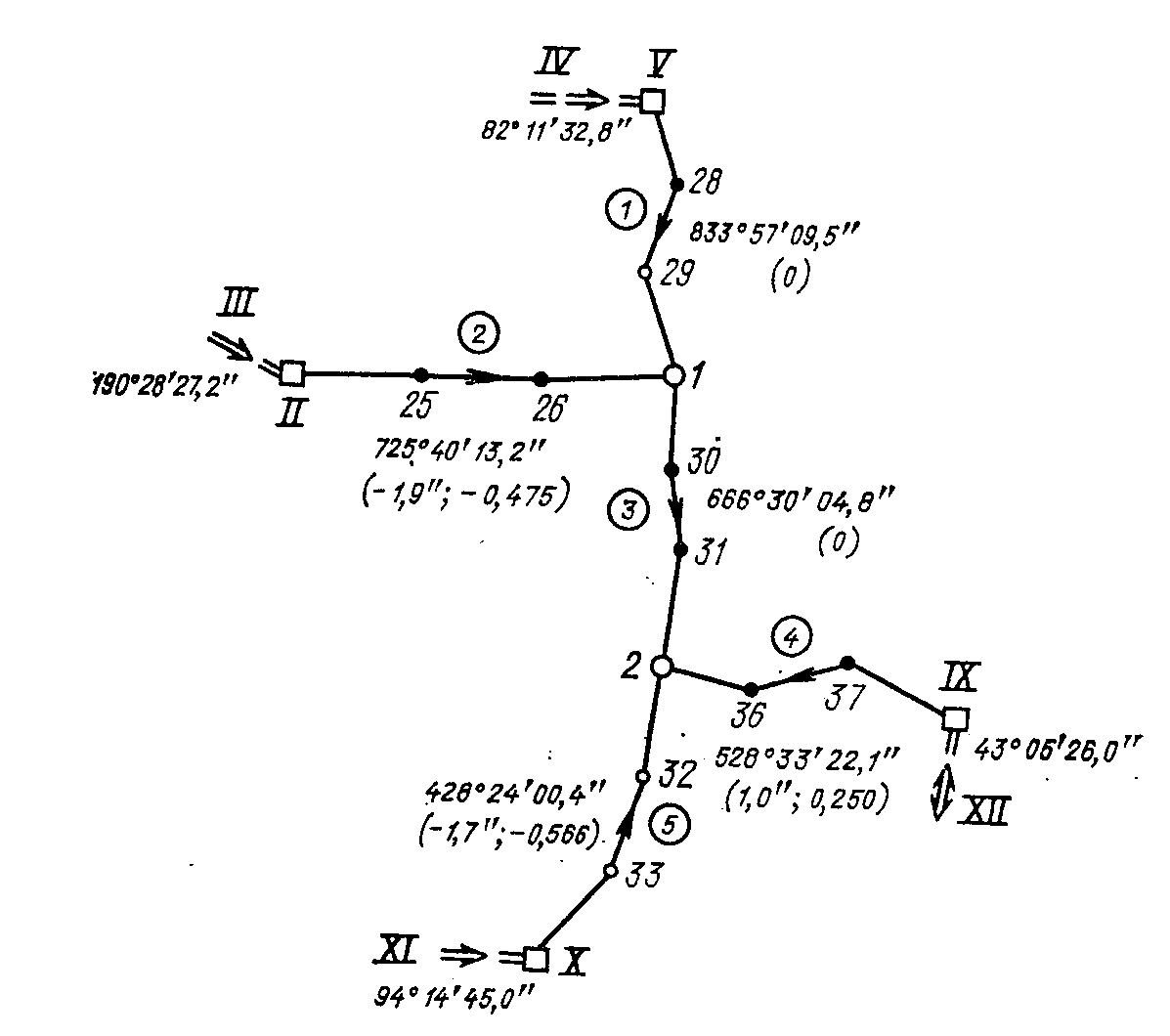
Рис. 59

Свободные члены уравнений поправок (фактически это невязки ходов, взятые с обратным знаком) вычисляем по формуле

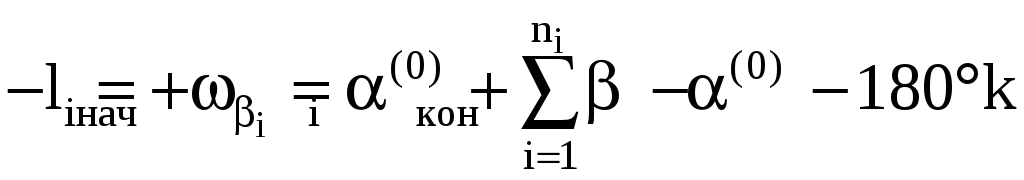
где k - такое число, при котором выполняется неравенство Ясно что по ходам 1 и 3 невязки равны 0. Нормальные уравнения составляем по способу узлов проф. В. В. Попова по формулам (3.75), (3.76) и (3.77) без составления уравнения поправок, так как коэффициенты перед неизвестными δα₁ и δα₂ как и в нивелирных сетях, равны ± 1 или 0. В общем виде нормальные уравнения будут

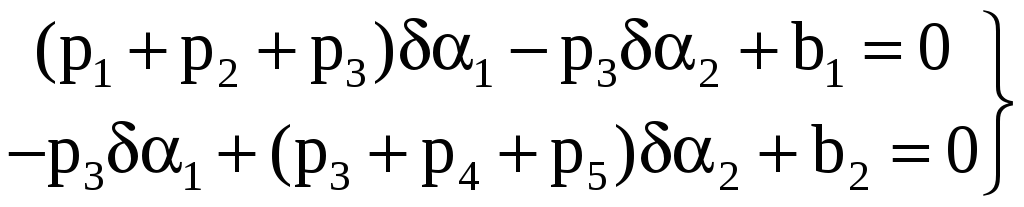
где свободные члены

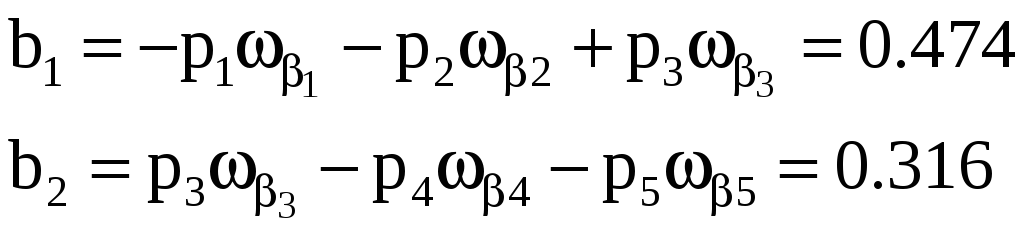
Величины и приведены в скобках на рис. 59. В результате вычислений получаем систему

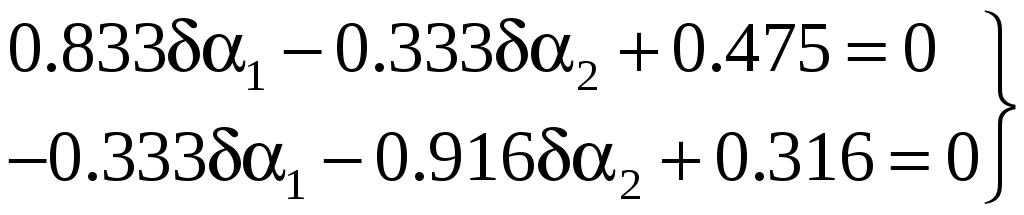
Решая ее путем обращения матрицы, находим

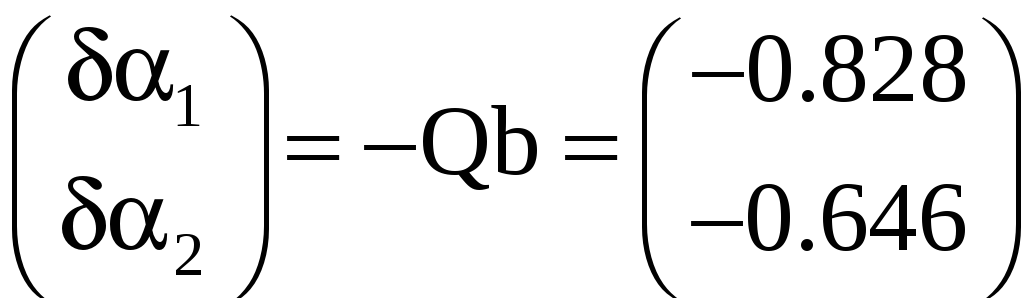
Далее для углов каждого хода вычисляем величины

( )

представляющие собой поправки в суммы углов ходов. Контроль вычислений вытекает из формулы [paυ] = [pbυ] = ... = 0 и приобретает вид

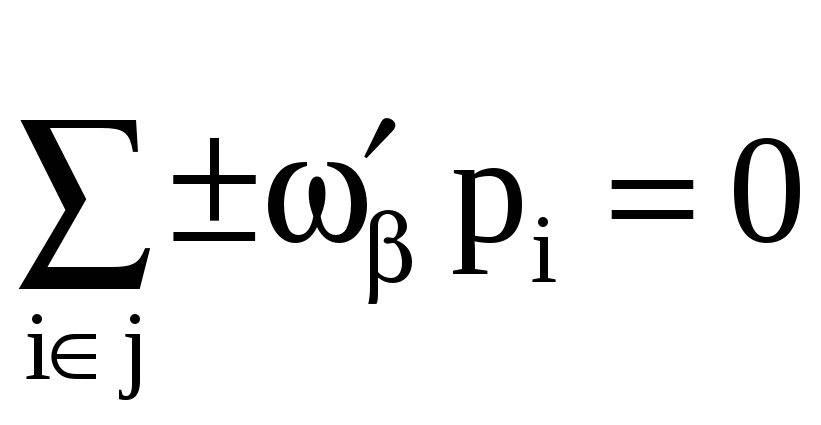
Соответственно для узлов 1 я 2 получаем

1) 0,207 - 0,268 + 0,060 = - 0,001,

2)- 0,060 + 0,411 - 0,351 = 0.

Поправки в углы в каждом ходе вычисляем по формуле

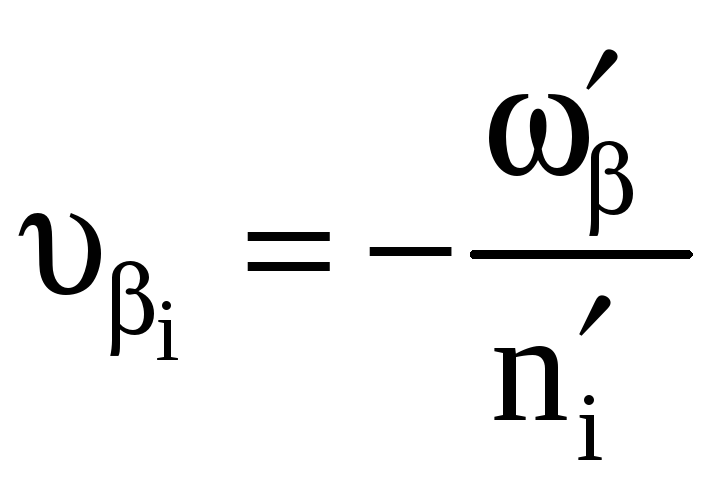
(здесь они не приводятся).

Далее по известным формулам вычисляем дирекционные углы всех сторон. Для оценки точности вычислим величину

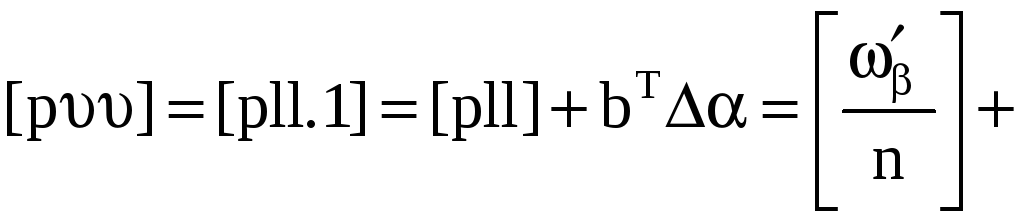
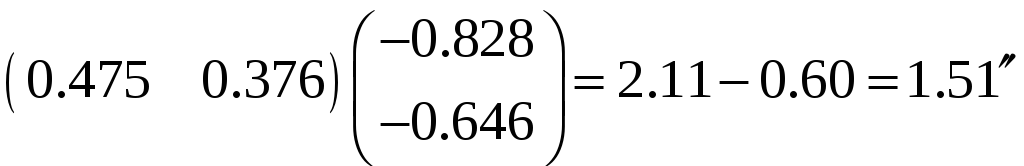
Средняя квадратическая ошибка измерения одного угла

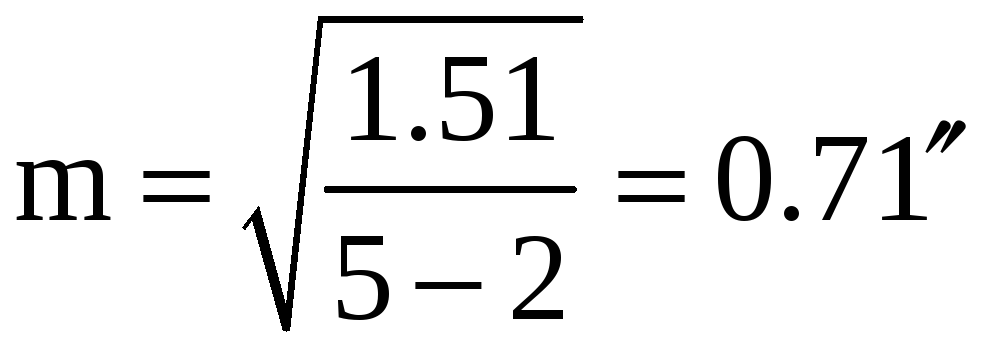а ошибка

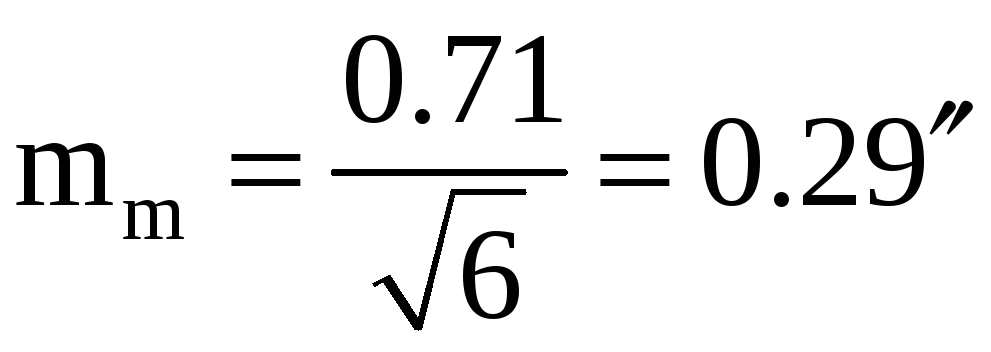
уравненных дирекционных углов

Коэффициент корреляции между ними

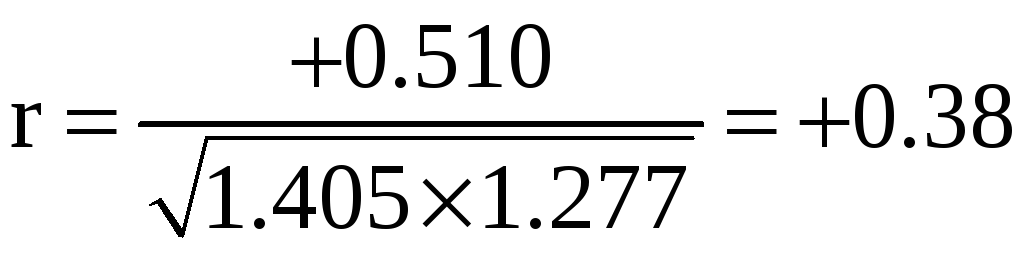
Если на узлах углы измерены способом круговых приемов, то им следует приписать вес, равный 2, а всем остальным углам - веса, равные 1. Тогда вес суммы углов хода с одним узлом найдем, исходя из формулы

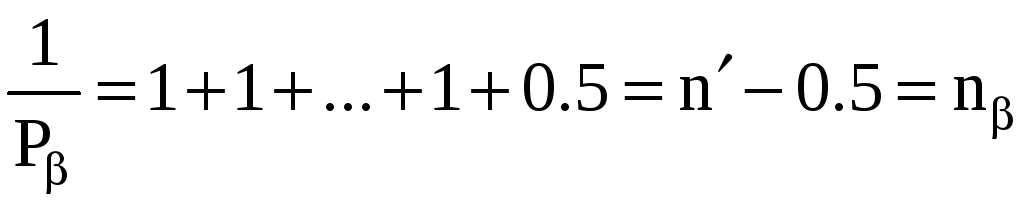
и вес

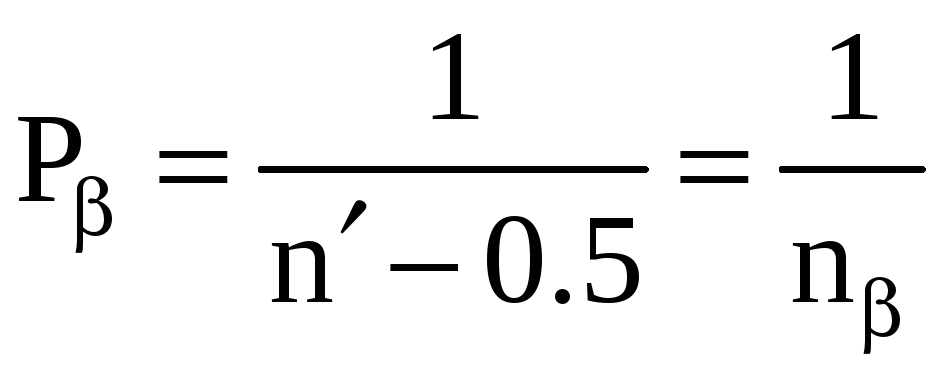
где, как и ранее, n' - число вершин хода, включая узловую точку. Для хода

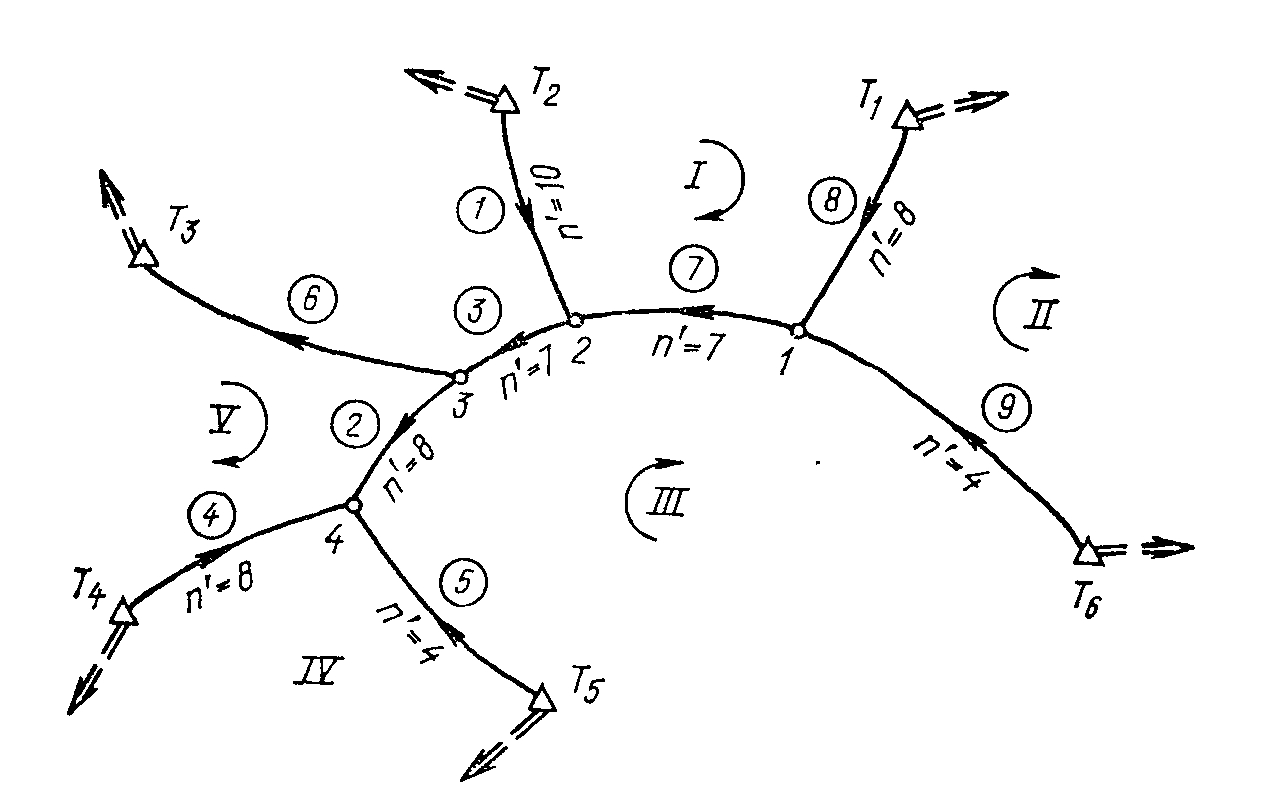
Рис. 60

«от узла к узлу» 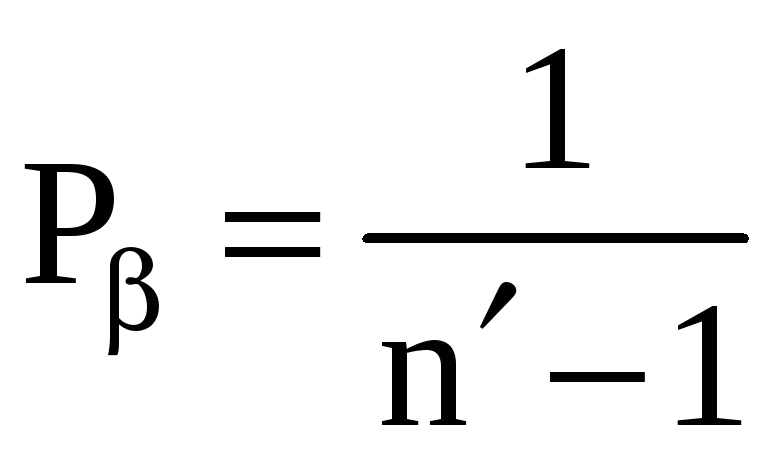. Все вычисления аналогичны выполненным ранее стой разницей, что поправки углов на узловых точках вычисляются по формуле

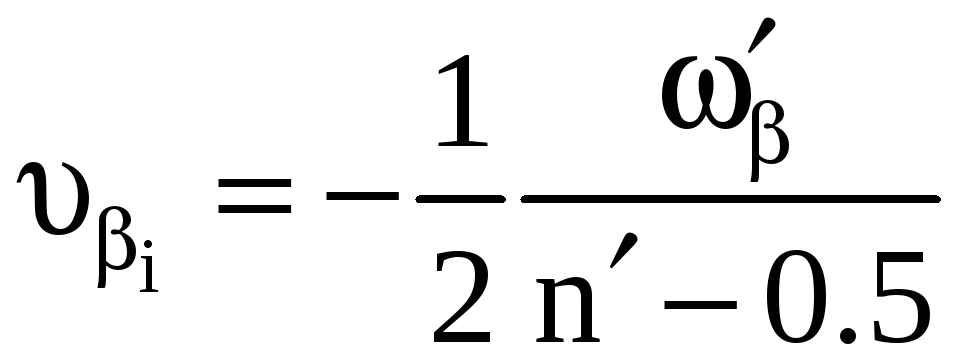
В этом случае получим матрицы

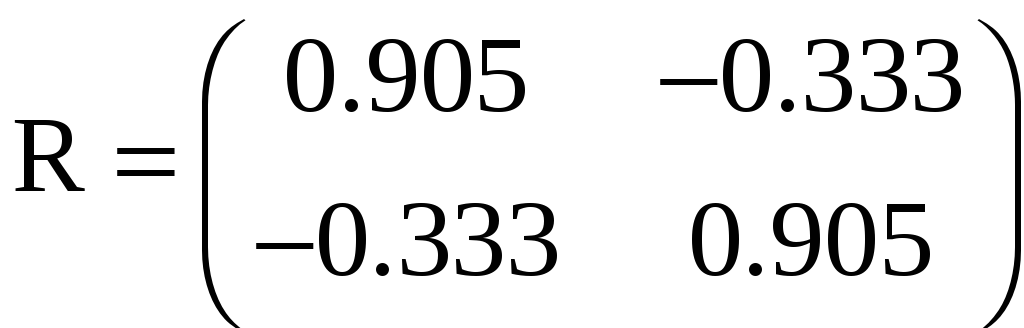
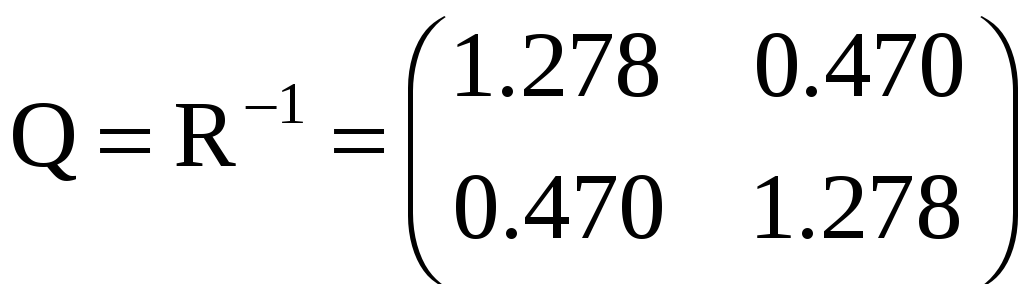
3.54. Составить матрицу коэффициентов нормальных уравнений, возникаю­щих при предварительном уравнивании полигонометрической сети (рис. 60), оценить точность уравненных дирекционных углов узловых направлений и вычислить коэффициенты корреляции между ними, если: 1) углы на узлах измерены отдельно друг от друга; 2) измерены способом круговых приемов.