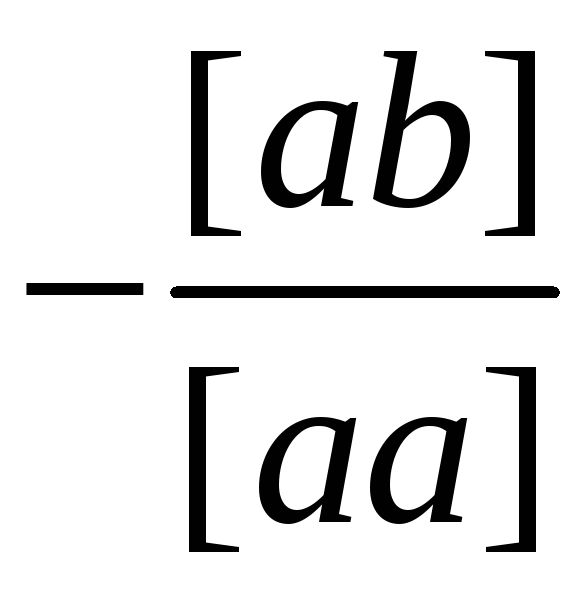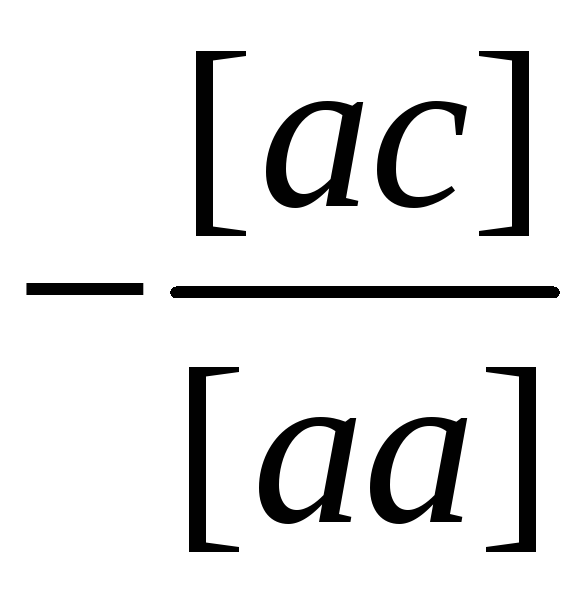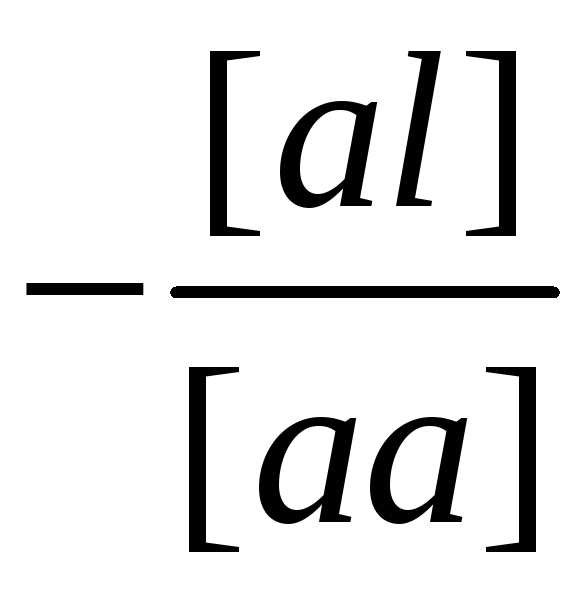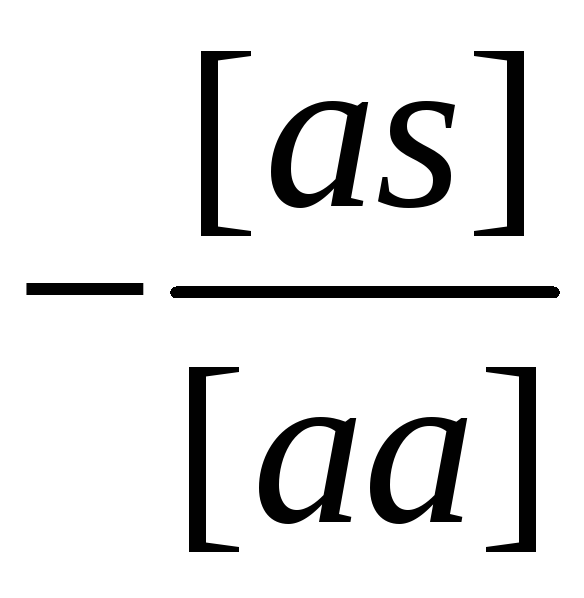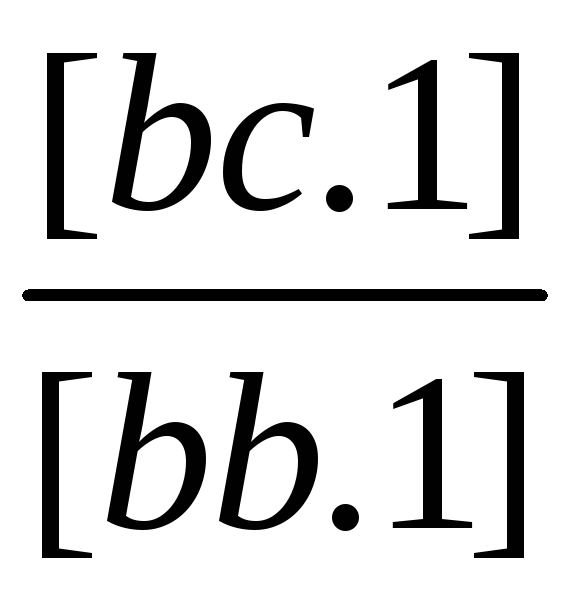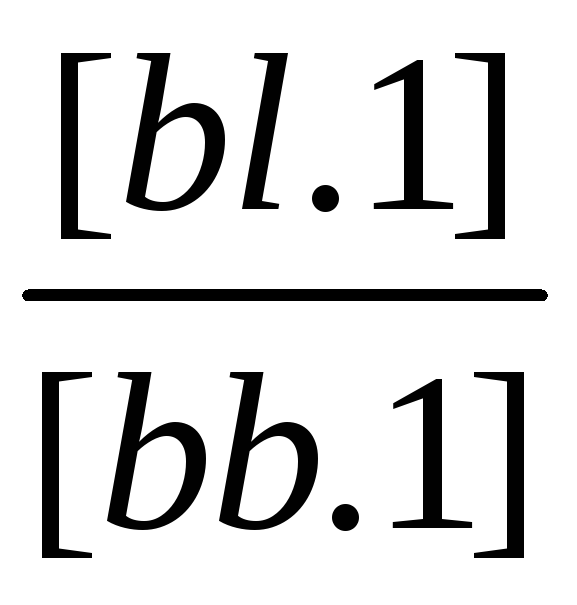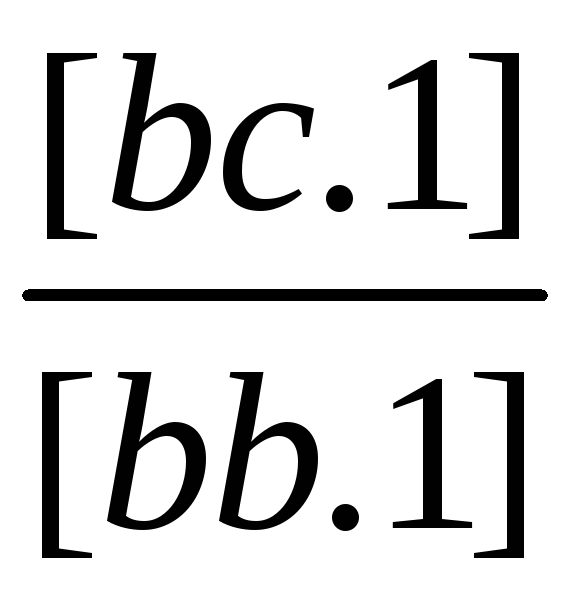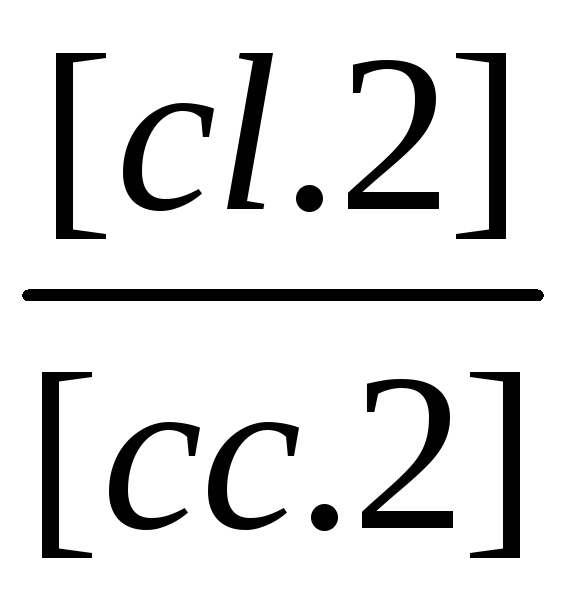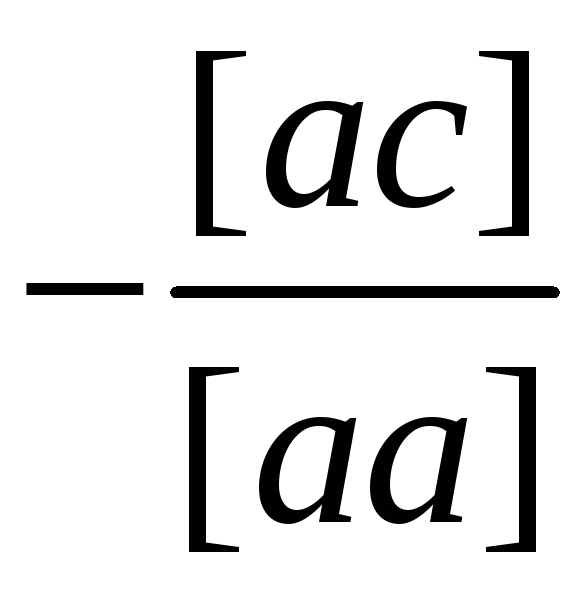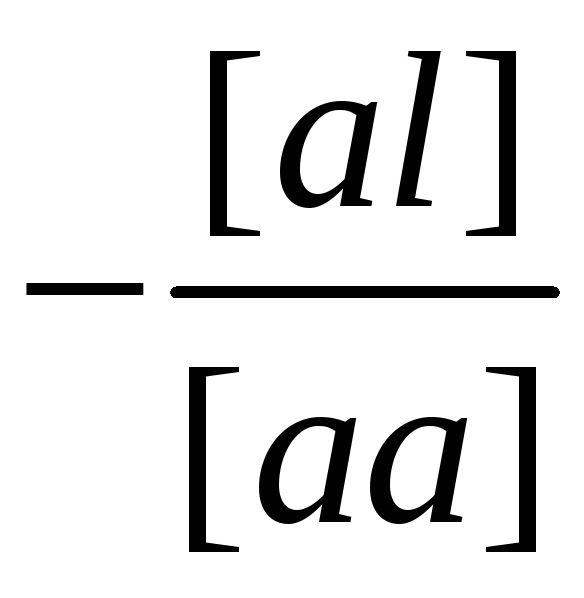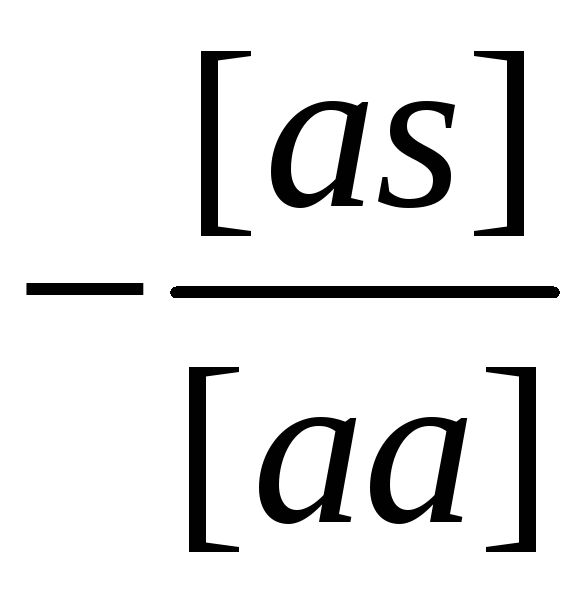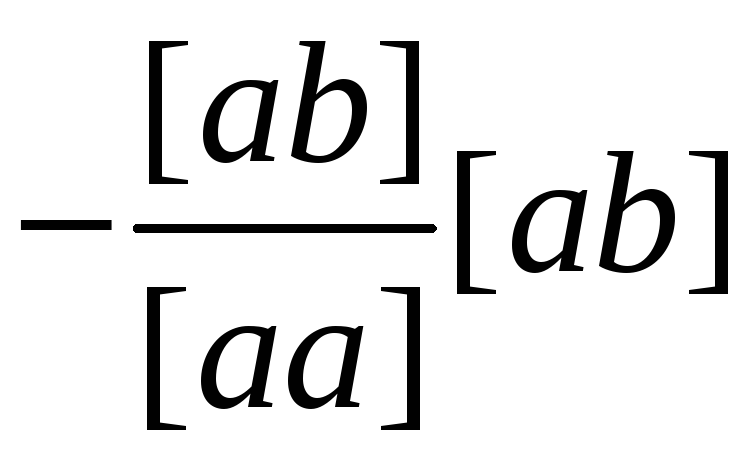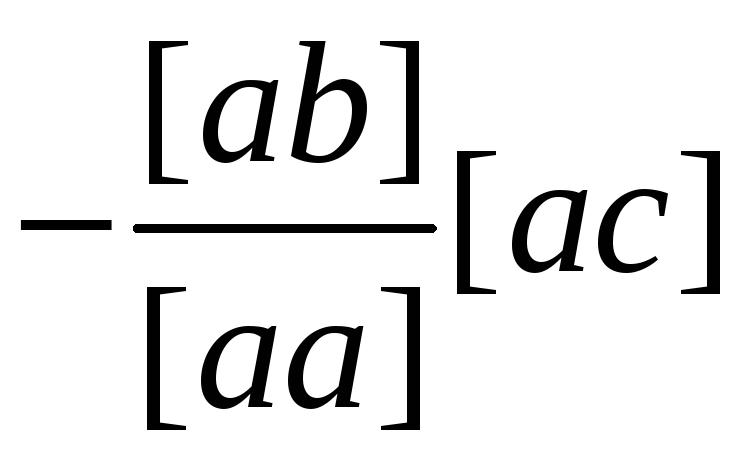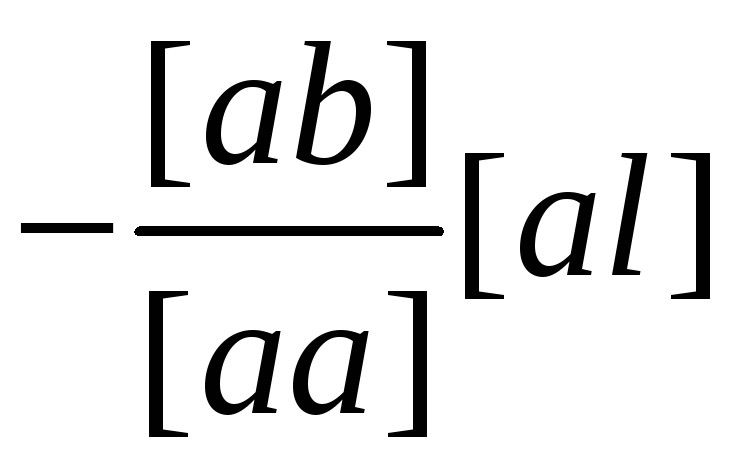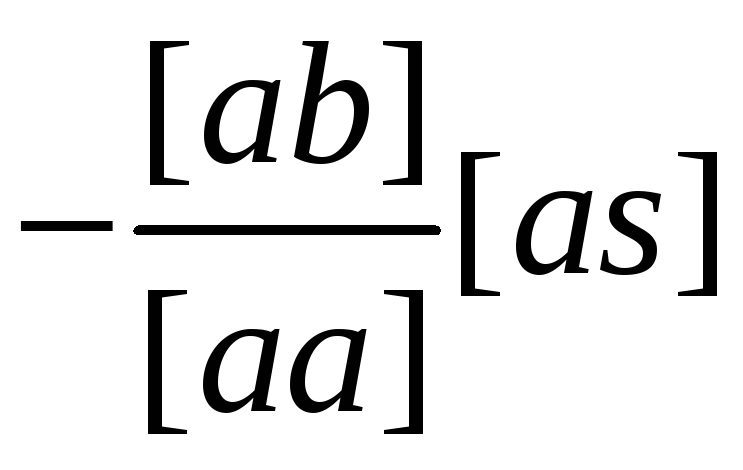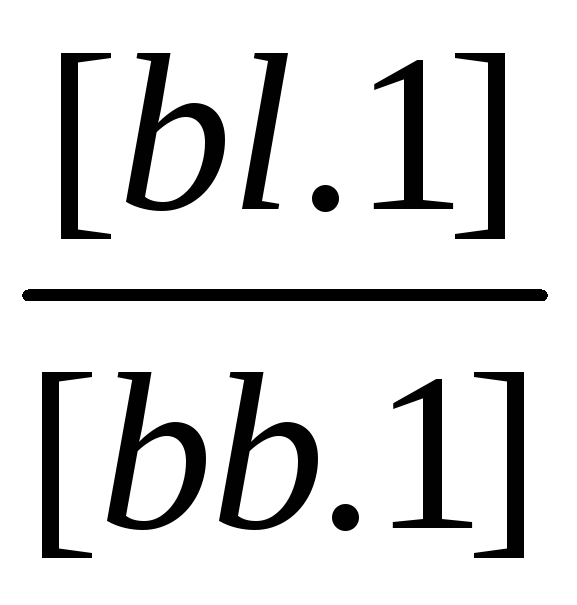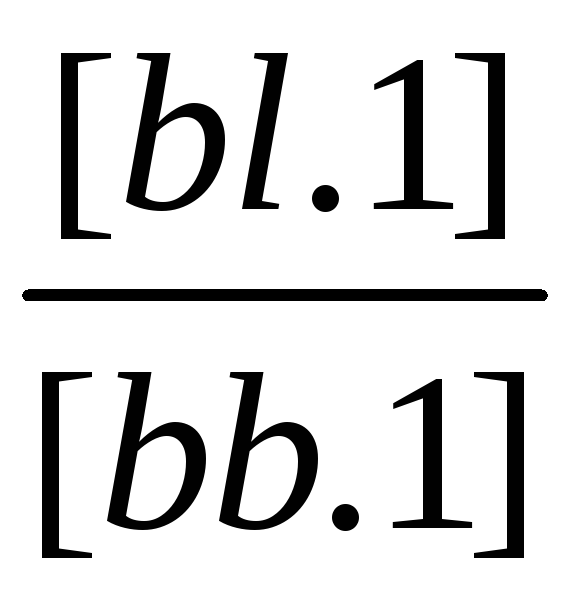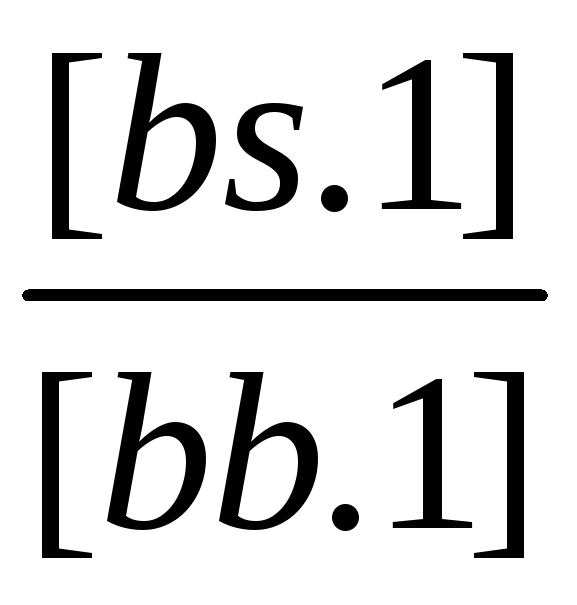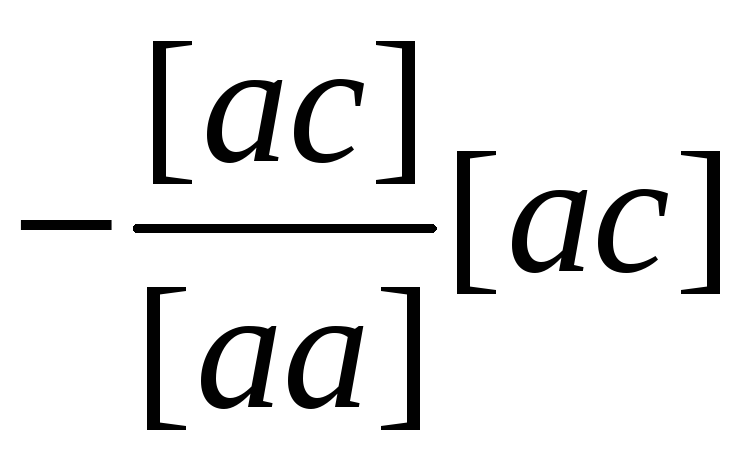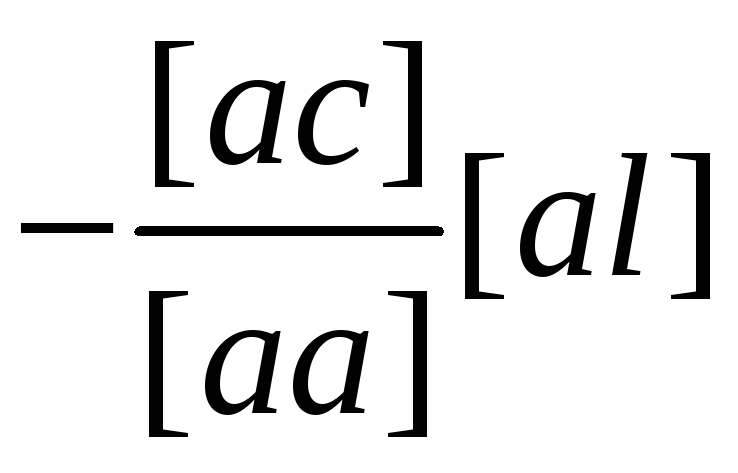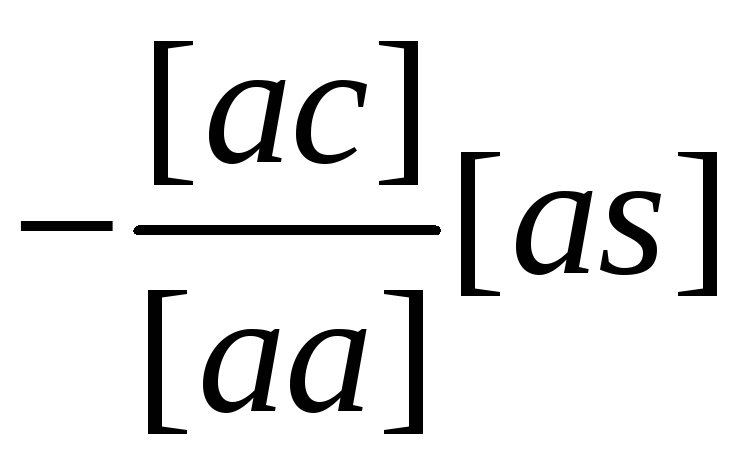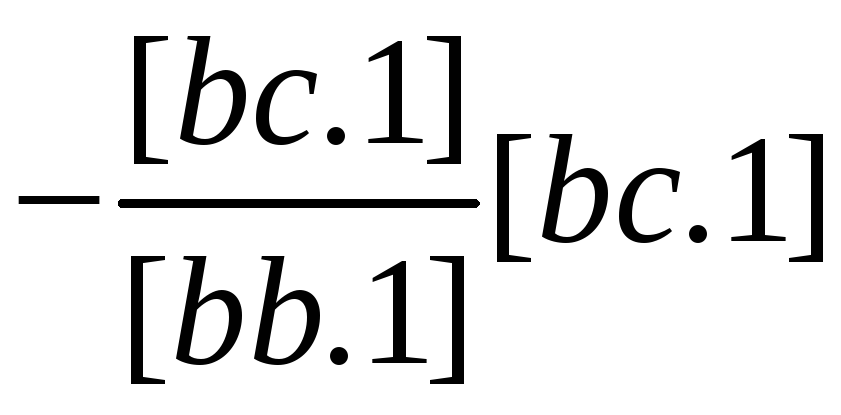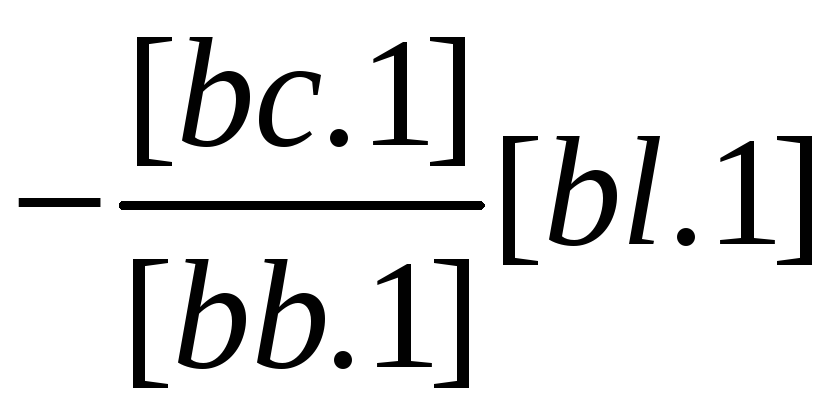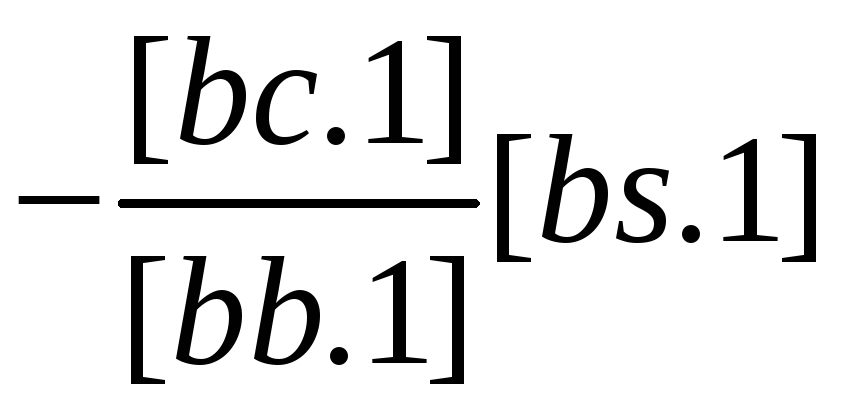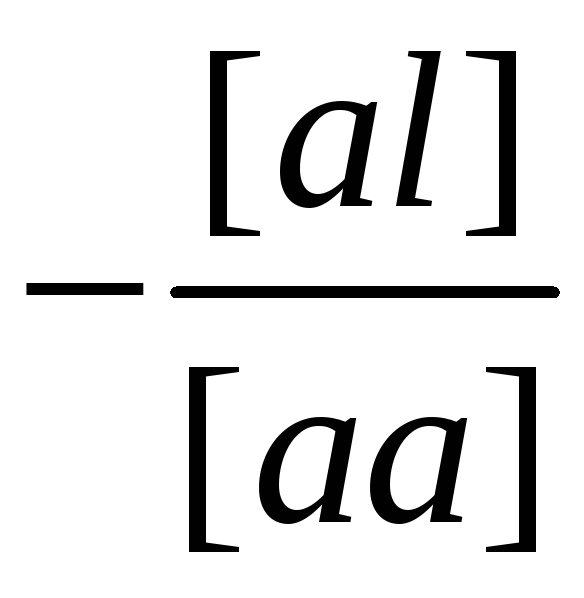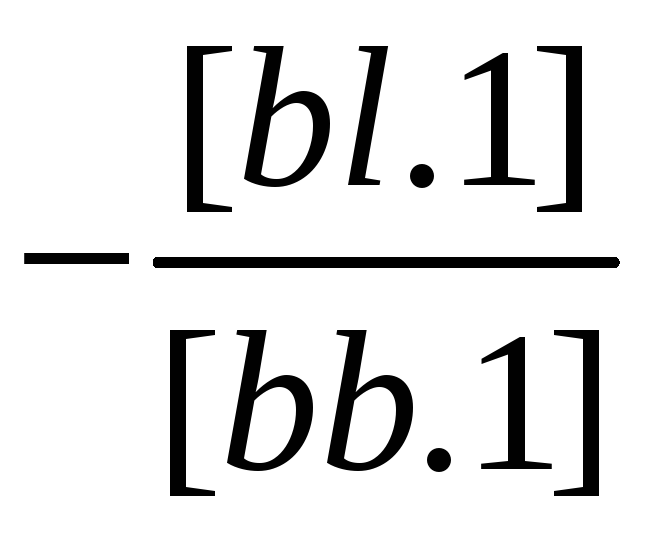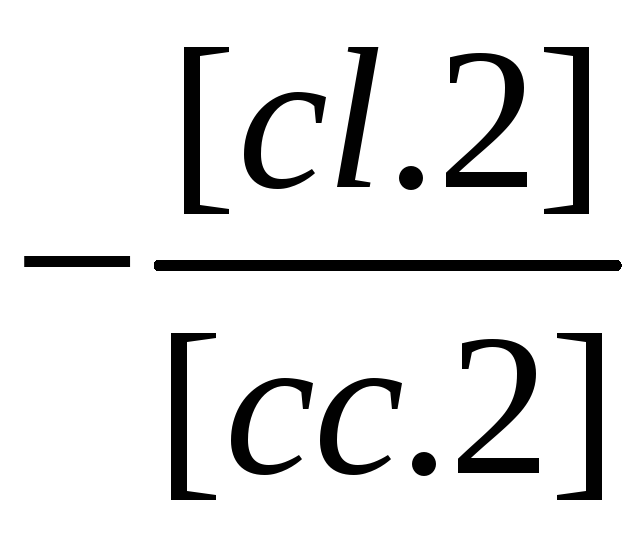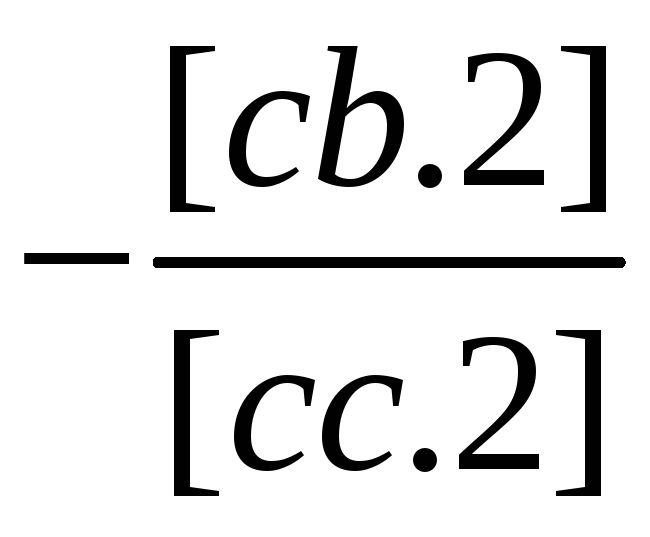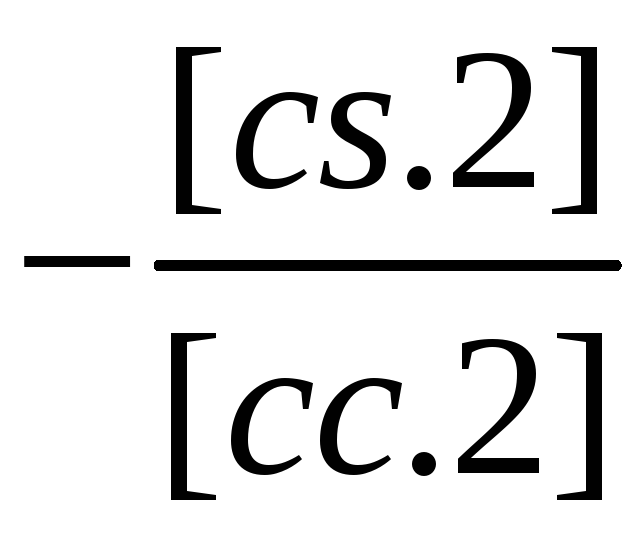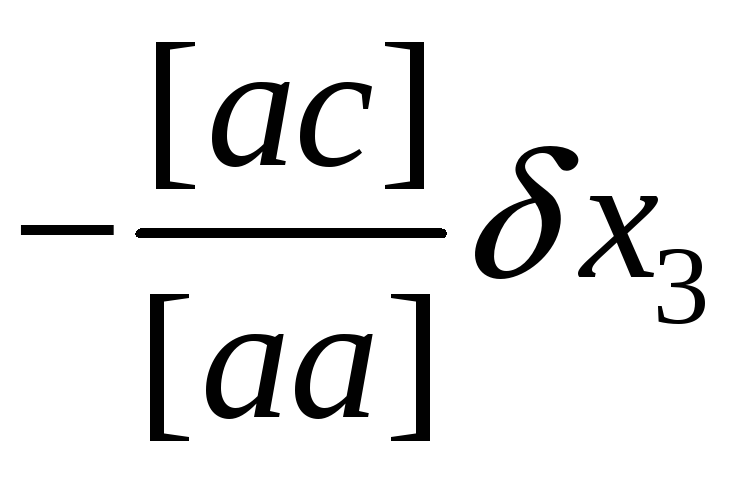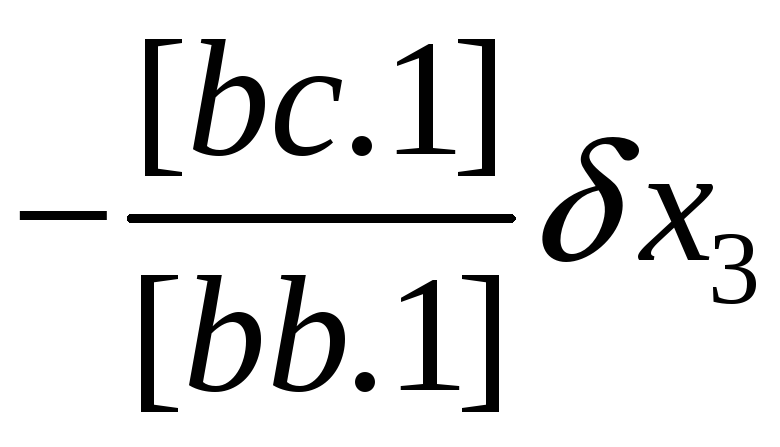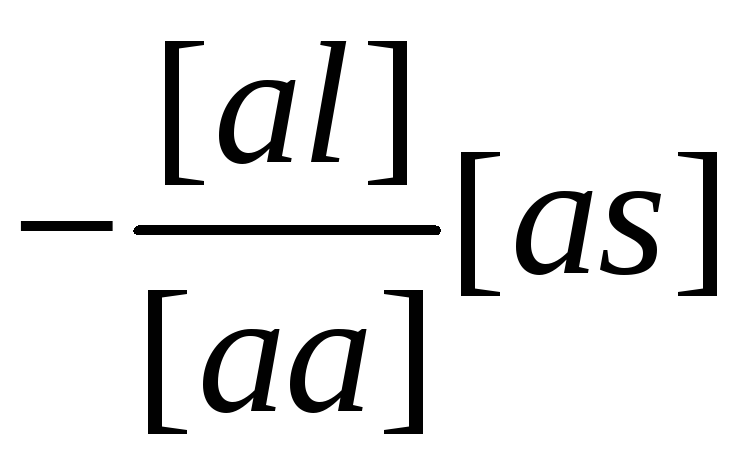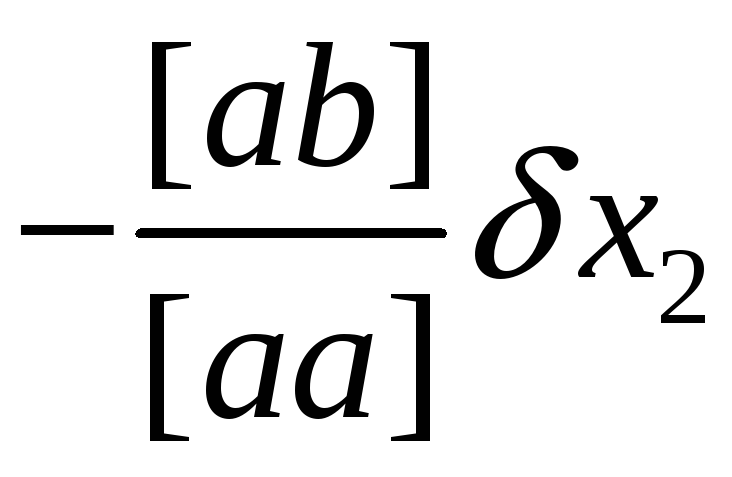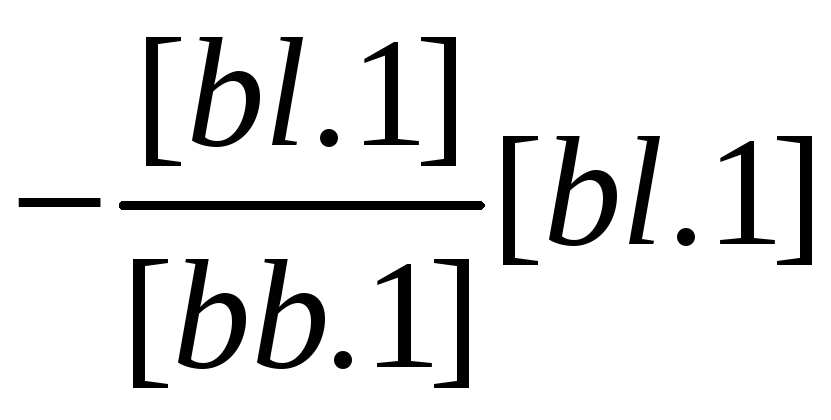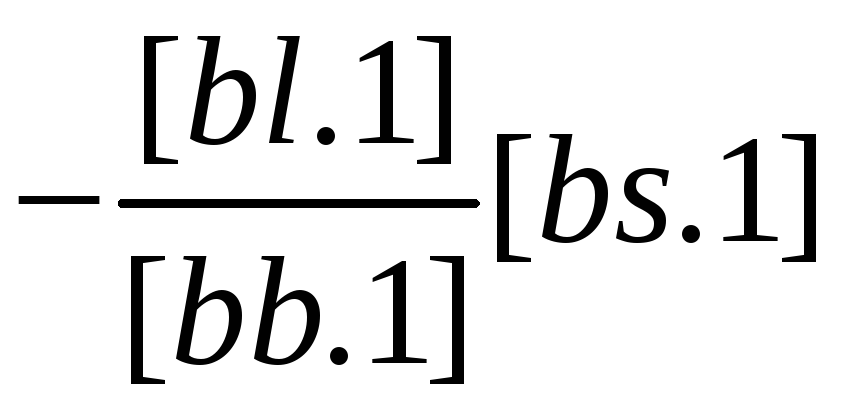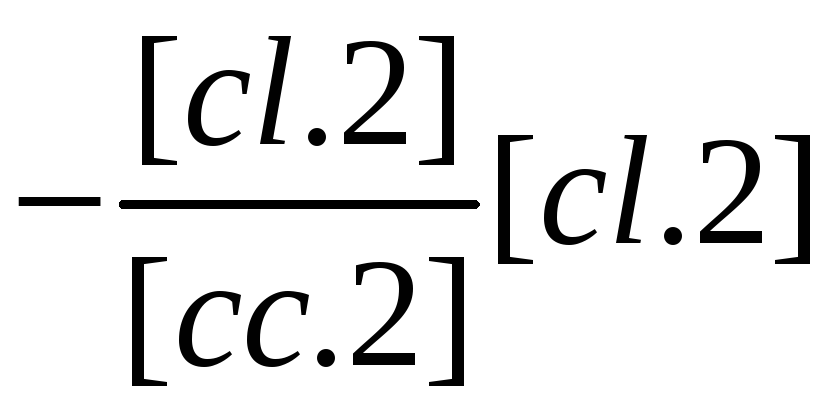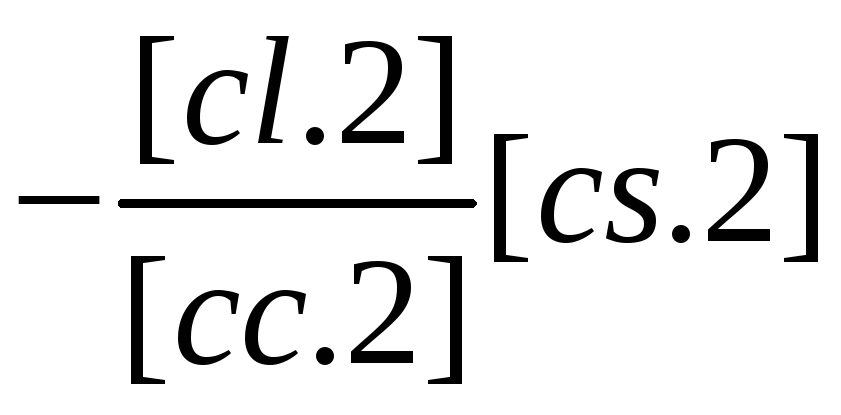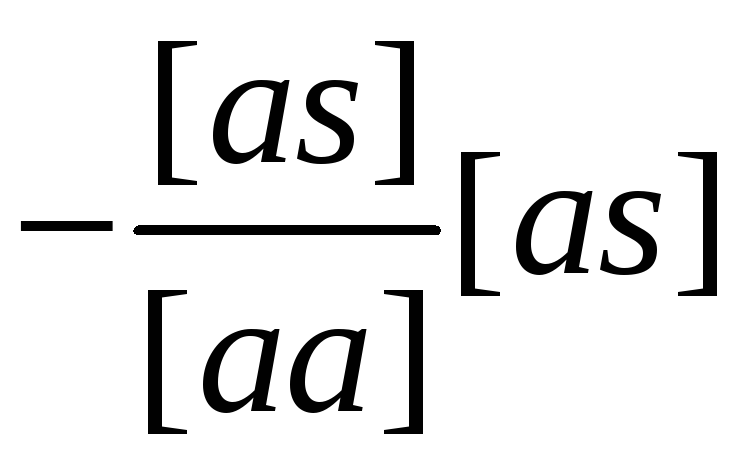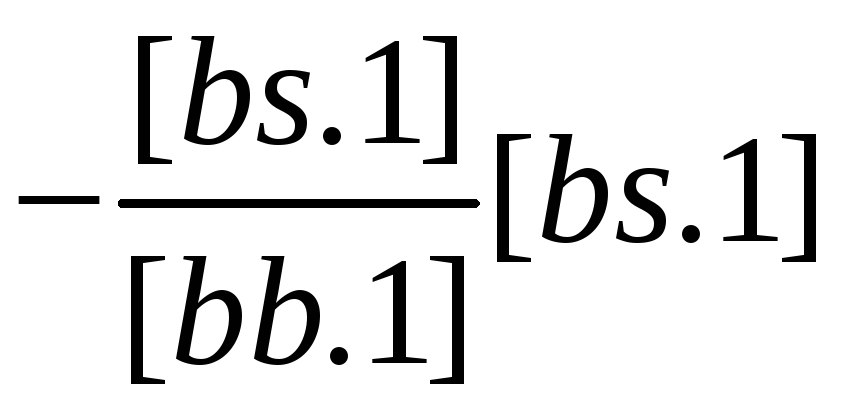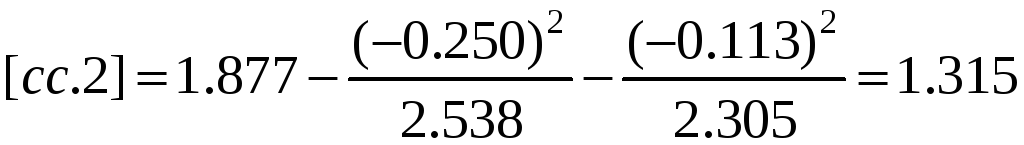
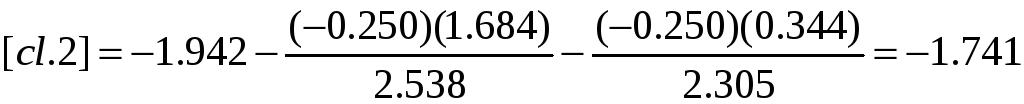
и третье эквивалентное уравнение

элиминационные уравнения

неизвестные

- 0.333, +0,443, + 1,226.

Подстановка полученных значений в исходную систему подтверждает правильность полученных результатов. Способ Гаусса удобен тем, что все вычисления удается расположить в компактной схеме, требующей выполнения однотипных вычислительных действий и позволяющей контролировать промежуточные результаты.

Контроль составления уравнений ошибок производится вычислением в две руки.

Контроль составления и решения нормальных уравнений произво­дится методом сумм:

(3.29)

причем

Коэффициенты нормальных уравнений и их свободные члены контролируют так:

(3.30)

Далее:

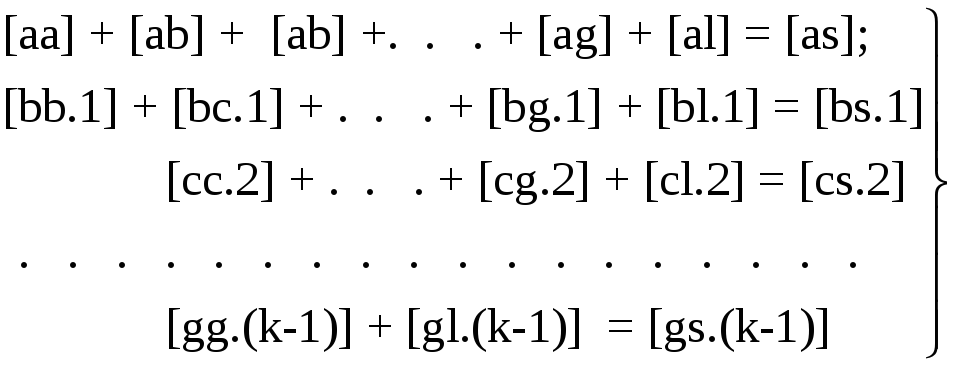(3.30^/)

Заключительным контролем прямого хода решения в схеме Гаусса является выполнение равенств

(3.31)

Затем переходят к вычислению неизвестных . По мере их вычисления контроль осуществляют путем вычисления вспомогательных неизвестных (см. ниже).

Получив все неизвестные, согласно (3.26) вычисляют по формуле (3.3) поправки v_i и контролируют на основе выражений

, , (3.32)

Проверяют также выполнение контрольных равенств

(3.33)

Справедливы равенства

(3.34)

Окончательным контролем решения задачи уравнивания является соблюдение равенств , которые следует проверить при нелинейных функциях (контролируется правильность разложения в ряд).

В линейных задачах достаточно ограничиться проверкой равенств (3.32), (3.33).

Составление нормальных уравнений при равноточных измерениях и их решение выполняют с помощью трех схем, приведенных для трех неизвестных.

Схема 1
Номера измерений	аi	bi	ci	li	si	vi
1	а1	b1	c1	l1	s1	v1
2	а2	b2	c2	l2	s2	v2
.	.	.	.	.	.	.
.	.	.	.	.	.	.
.	.	.	.	.	.	.
n	аn	bn	cn	ln	sn	vn
	[a]	[b]	[c]	[l]	[s]	[v]
	[av]	[bv]	[cv]			[v2]

Схема 2
Номера измерений	а]	b]	c]	l]	s]	Контроль
a]	[aa]	[ab]	[ac]	[al]	[as]	Расхож- дение до 0.01
b]		[bb]	[bc]	[bl]	[bs]
c]			[cc]	[cl]	[cs]
l]				[ll]	[ls]
s]					[ss]

Схема З
				l	s	Контроль
(1/[aa])	[aa]	[ab]	[ас]	[al]	[as]
	(-1)
(1/[bb.1])		[bb.1]	[bc.1]	[bl.1]	[bs.1]
		(-1)
(1/[сс2])			[cc.2]	[cl.2]	[cs.2]
			(-1)
				[ll.3]	[ls.3] [ss.3]

При небольшом числе неизвестных (k < 10) коэффициенты нормальных уравнений часто вычисляют до 0,01-0,001. С такой же точностью вычисляют и коэффициенты эквивалентных уравнений. Коэффициенты же элиминационных уравнений и неизвестные вычисляют до 0,001-0,0001. Величины 1/[аа], 1/[bb.1] и т. д. в схеме 3 введены для замены действия деления умножением. Их вычисляют до 0,0001.

Расхождение контрольных сумм эквивалентных строк в схеме Гаусса допускают до 0,01-0,02 (допуск увеличивается по мере спуска вниз по схеме). Заметим, что в столбец s выписаны числа из столбца «контроль» схемы 2.

Схема 3 представляет собой сокращенную схему Гаусса, в которой опущены промежуточные записи, связанные с раскрытием алгоритмов. Все алгоритмы Гаусса в этой схеме получаются методом накопления на счетчиках механических или электрических вычислительных машин. Если выполнить порядковую нумерацию строк в схеме 3, опустив элиминационные строки, то можно сформулировать следующее правило вычисления коэффициентов этих строк: любой коэффициент, расположенный в i-й строке и j-м столбце схемы, равен соответствующему коэффициенту из схемы 2 плюс сумма произведений уже полученных чисел элиминационных строк из столбца i на числа из столбца j, расположенные над ними (в эквивалентных строках). Например, [cs.2] получим как [cs] плюс сумма произведений чисел элиминационных строк из столбца с (-[ас/[аа] и -[bc.l]/[bb.l] соответственно на числа [as] и [bs.1] (числа эквивалентных строк из столбца s). Неизвестные δx_j вычисляются по следующему правилу:

Схема 3
δx1	δx2	δx3	l	s	контр.
[aa]	[ab]	[ac]	[al]	[as]
-1
	[bb]	[bc]	[bl]	[bs]
	[bb.1]	[bc.1]	[lc.1]	[ls.1]
	-1
		[cc]	[cl]	[cs]
		[cc.2]	[cl.2]	[cs.3]
		-1
			[ll]	[ls]
		δx3
	δx2

Продолжение схемы 3
δx1
			[ll.3]	[ls.3]
				[ss.3]
				[ss.3]

неизвестное δx с номером j равно числу j-й элиминационной строки из столбца l плюс сумма произведений уже вычисленных неизвестных δx на расположенные над ними числа из этой же элиминационной строки.

Приводим также полную так называемую «школьную» схему Гаусса (схема 4) лишь с целью разъяснения порядка вычислений при раскрытии алгоритмов Гаусса. Однако следует отметить, что необходимость выполнения записей промежуточных вычислений может внести только дополнительные ошибки и увеличить время вычислений. Поэтому сразу необходимо приучить себя к применению метода накопления, т. е. пользоваться сокращенной схемой.

В прил. XIII.10 и XIII.11 приводятся программы для калькулятора «Электроника БЗ-21» вычисления выражений вида [x²], [ху] и перемножения строки с на матрицу А, что обеспечивает автоматизацию составления и решения нормальных уравнений и вычисления поправок.

Контроль вычисления неизвестных δx_j можно осуществить путем подстановки их в j-е эквивалентные уравнения (3.25). Для того чтобы судить о влиянии ошибок округления, неизвестные следует подставить в исходную систему нормальных уравнений (это целесообразно делать при большом числе неизвестных). Если отклонения от нуля в правых частях ε_j окажутся существенными, то следует неизвестные уточнить, решая систему со свободными членами, равными ε_j.

Существует также иной надежный способ текущего контроля вычисления всех неизвестных δx_j, начиная с последнего. Напишем выражения (3.29) в матричной форме

(3.35)

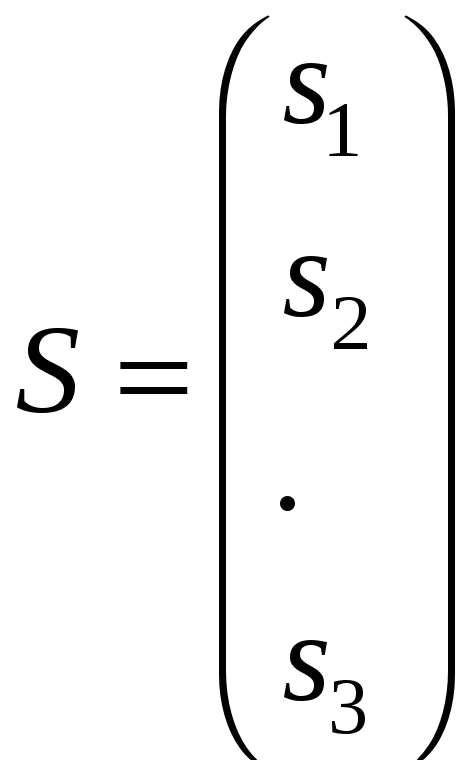
где векторы

;

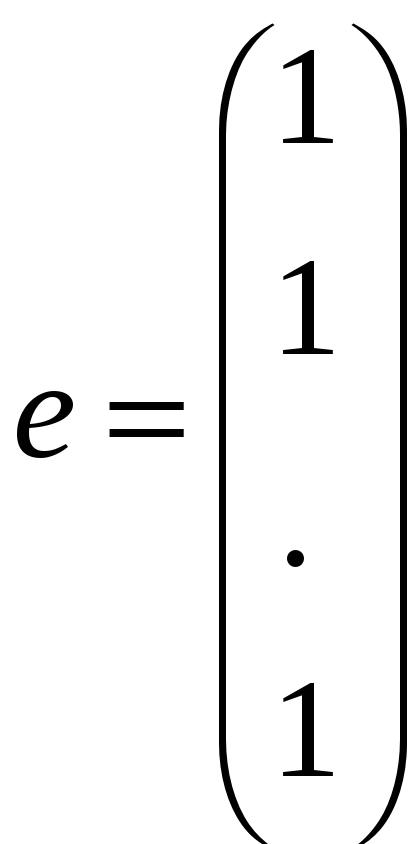называются соответственно суммирующим и суммарным. Умножая (3.35) слева на матрицу А^Т , получим систему нормальных уравнении

(3.36)

относительно неизвестных е_j = 1. Из сравнения системы (3.36) с системой нормальных уравнений (3.19), для которых справедливы эквивалентные уравнения (3.25), так как обе системы нормальных урав­нений имеют одну и ту же матрицу R, сразу следуют контрольные равенства (3.30')· Далее, вычитая из (3.19) систему (3.36), находим

(3.37)

где вектор

(3-38)

Отсюда следует, что если столбец свободных членов А^TL заменить суммарным столбцом А^TS и оставить для его элементов условно прежние обозначения [al], [bl]...[gl], то вместо δx_j будем получать неизвестные поэтому

(3.39)

что следует из (3.38).

Формула (3.39) позволяет проверить δx_j, не дожидаясь, пока будут вычислены все неизвестные, а подстановка их в исходную систему нормальных уравнений обнаружит ошибку в вычислениях слишком поздно. Заметим, что уклонения от 1 в формуле (3.39) допустимы до 0,005 при вычислении неизвестных с точностью до 0,001.

Решим теперь систему нормальных уравнений (см. схемы 2 и 3), приведенную в примере (стр. 149) в схеме Гаусса (получение этой системы здесь не приводится).

Схема 2
δx1	δx2	δx3	l	s
2,583	-1,167 2,833	-0,250 -1,000 1,877	1,684 -0,418 -1,942	2,850 0,248 -1,315
			13,126	12,450 14,233

Схема 3
(0,3871)	2,583 -1	-1,167 0,452	-0,250 0,097	1,684 -0,652	2,850 -1,103	2,850 -1,103
(0,4336)		2,306 -1	1,113 0,483	0,344 -0,149	1,536 -0,666	1,537 -0,666
(0,7604)			1,315 -1	- 1,612 1,226	-0,297 0,226	-0,297 0,226
δxj	-0,333	0,443	1,226	10,000	9,999	-[ls.3]
δxj Контроль	- 1,333 1	-0,557 1	0,226 1	[11.2]	9,999 [ss.3]

Таблица 40

Номера углов	Углы	Измеренные значения	Неизвестные	Уравненные значения
1 2 3 4 5 6	АОВ BOC COD АОС BOD AOD	38° 31’ 15,5" 46 07 30,0 17 43 46,5 84 38 45,0 63 51 16,5 102 22 33,0	x1 x2 x3 x1 + x2 x2 + x3 x1 + x2 +x3	38° 31’ 15,62" 46 07 29,88 17 43 46,87 84 38 45,50 63 51 16,75 102 22 32,37

3.17. В табл. 40 даны результаты измерения углов во всех комбинациях (рис. 45). Уравнять эти результаты параметрическим способом.

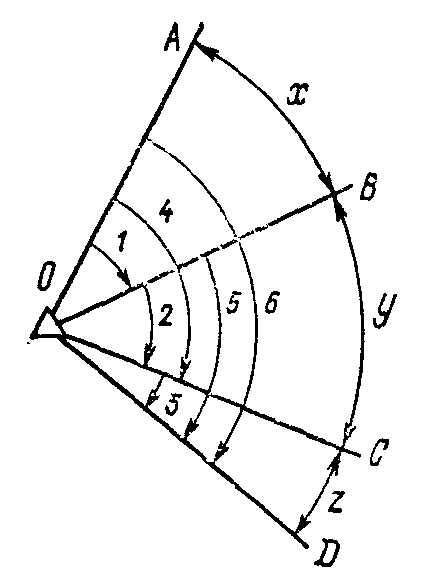
Рисунок 45

Решение. 1) Выберем в качестве независимых неизвестных (параметров) Х₁ Х₂, Х₃ соответственно первый, второй, третий углы. Тогда остальные три угла, зависящие от первых трех, будут представлять собою суммы независимых неизвестных. Уравнения связи имеют вид

Y₁ = Х₁ Y₄ = Х₁ + Х₂

Y₂ = Х₂ Y₅ = Х₂ + Х₃

Y₃ = Х₃ Y₆ = Х₁ + Х₂ + Х₃

2) Записываем уравнение поправок в общем виде

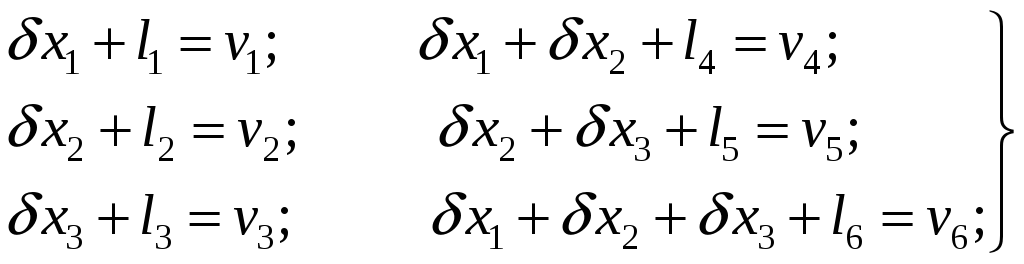(3.40.)

3) Введем приближенные значения неизвестных, приняв их равными измеренным значениям углов х₁, х₂, x₃,

x₁⁽⁰⁾ = 38° 31' 15,5"; х₂⁽⁰⁾ = 46° 07' 30,0"; x₃⁽⁰⁾ = 17° 43' 46,5"

4) На основании (3.4) вычислим свободные члены l_i как разности приближенных значений углов и измеренных. Получаем

l₁ = 0; l₄ = 0.5"

l₂ = 0; l₅ = 0"

l₃ = 0; l₆ = - 0.5"

5) По уравнениям (3.40) составим таблицу коэффициентов уравнений поправок и нормальных уравнений (табл. 41, 42').

Таблица 41
номера измерений	коэффициенты				s	v
	a	b	c	l
1	1				1	0,12
2		1			1	-0,12
3			1		1	0,37
4	1	1		0,5	2,5	0,50
5		1	1		2,0	0,25
6	1	1	1	-1,0	2,0	-0,63
Σ	3	4	3	-0,5	9,5	[vs]=0,86
δxj	0,124	-0,122	0,373	[lv]=0,88	[v2]=0,874
	[av]	[bv]	[cv]
	-0,01	0	0

6) Затем решим нормальные уравнения (табл. 43).

Как видим, все предусмотренные контроли выполняются. Уравненные значения углов приведены в таб. 40 в последнем столбце.

Окончательным контролем решения задачи является выполнение равенств в чем легко убедиться непосредственной проверкой.

Τаблица 42
	a]	b]	с]	d]	S]	Контроль
[a [b [с	3,00	2,00 4,00	1,00 2,00 3,00	-0,50 -0,50 -1,00	5,50 7,50 5,00	5,50 7,50 5,00
[l [s				1,25	-0,75 17,25	-0,75 17,25

Вспомогательные величины	δx1	δx2	δxj	l	s	Контроль
(0,3333)	3,00 (-1)	2,00 -2,667	1,00 -0,333	-0,50 0,167	5,50 -1,833	5,50 -1,833
(0,3745)		2,67 (-1)	1,33 (-0,498)	-0,17 0,064	3,83 -1,434	3.83 - 1,434
(0,5000)			2,00 (-1)	-0,75 0,373	1,26 -0,627	1,25 -0,627
	0,124 -0,875 0,999	-0,122 0,878 1,000	0,373 -0,621 1,000	0,88	0,89 0,89

30 Оценка точности уравненных неизвестных

В методе наименьших квадратов доказывается, что обратные веса уравненных неизвестных

(3.41)

где Q_jj - так называемые весовые коэффициенты. Они являются диагональными элементами матрицы

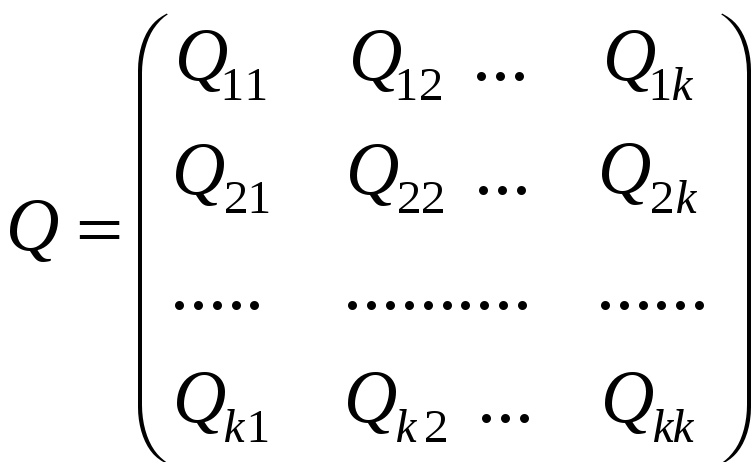(3.42)

получаемой обращением матрицы R, т. е. Q = R^-1. Так как RQ = E то, обозначив j-й столбец матрицы Q через Q_j, а матрицы Ε – череp E_j, получим k систем нормальных уравнений вида

(3.43)

Как видно, системы (3.43) и (3.19) имеют одну и ту же матрицу коэффициентов R. Отсюда следует, что для вычисления элементов столбцов Q_j матрицы Q в схему Гаусса необходимо дополнительно ввести столбцы – Е_j, равные

, ,

и, рассматривая их как новые столбцы свободных членов, по каждому из них получить k столбцов Q_j. Более того, если каждый из столбцов – E_j условно обозначить как столбец свободных членов

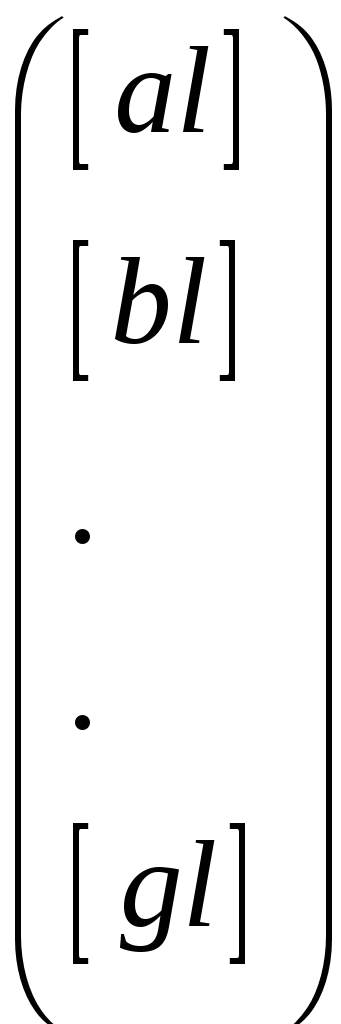
то элементы столбцов Q_j получим по тем же формулам, что и .неизвестные δx_j.

Так, в задаче 3.17 вычисление величин Q_jj приведем в табл. 44.

Контролем вычислений являются равенства Q_ij = Q_ji, так как матрица Q, как и R, симметричная. Обычно при вычислениях табл. 43 и 44 совмещают, помещая столбцы - E_j вслед за столбцом «контроль» в табл. 43, а элементы Q_ij, ниже строки «контроль» в левой нижней части этой таблицы.

Таблица 44
δx1	δx2	δx3	-Ε1	-Ε2	-Ε3
3,00 -1,00	2,00 -0,667	1,00 -0,333	- 1 0,333	0 0	0 0
	2,67 - 1,000	1,33 -0,498	0,67 -0,251	-1,00 0,374	0 0
		2,00 - 1,000	0 0	0,50 -0,250	- 1,00 0,500

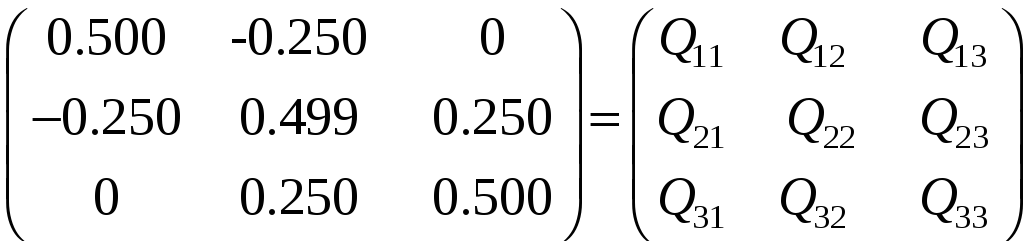
Приведем дополнительно способ вычисления любого элемента матрицы Q, не требующего знания остальных ее элементов. Он основан на следующих соображениях.

Матрицу коэффициентов нормальных уравнений всегда можно представить в виде произведения двух треугольных матриц Т₁ и Т₂

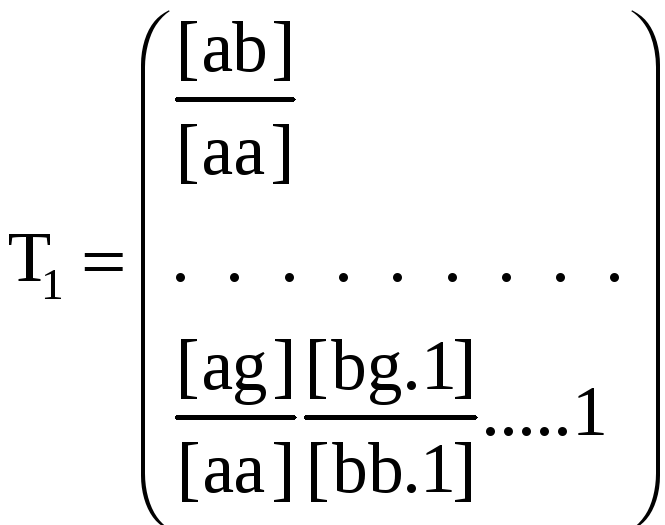
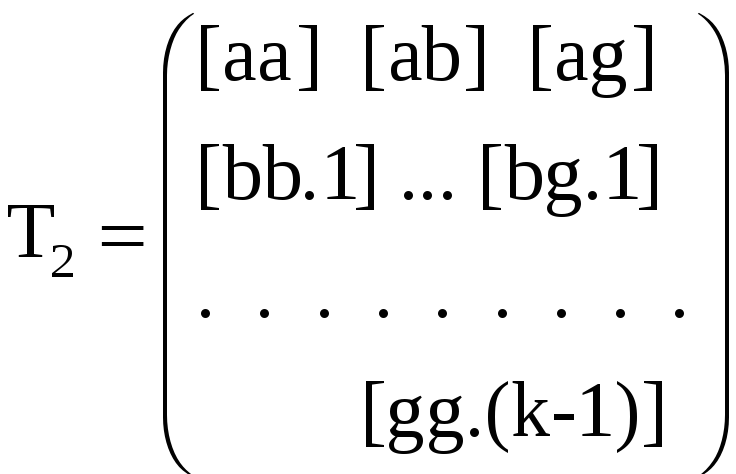
составленных из элементов элиминационных строк, взятых с обратным знаком, и эквивалентных строк схемы Гаусса. Собственно на этом представлении и основан способ Гаусса. Так как RQ = Е, то полу­аем T₁T₂Q = Ε, откуда следует

Можно показать, что элементы матриц Τ^-1₁ и Т^-1₂ как раз и содержатся в столбцах Ε_j таблиц: в нечетных строках с обратным знаком элементы матрицы Τ^-1₁, а в четных - элементы матрицы (Τ^-1₂)^Т .Так, в нашем примере

Перемножив эти матрицы, получим матрицу Q. Но вычисления удобно выполнять в таблице вида табл. 44 по следующему правилу: любой элемент Q_ij матрицы Q равен взятой с обратным знаком сумме произведений чисел всех элиминационных строк из столбца – Ε_i на элементы эквивалентных строк из столбца – E_j (так называемый способ диагоналей). Например, Q₁₁ = - (0,333-0,67 X 0,251) = 0,500, Q₂₂ = (0,374 - 0,250 Χ 0,50) = 0,500, Q_i2 = - 0,251 и т. д. Средние квадратические ошибки уравненных неизвестных вычисляют по формуле где для равноточных измерений· средняя квадратическая ошибка одного измерения вычисляется по формуле (обобщение формулы Бесселя, получаемой при k = 1). Так, в задаче 3.17 = 0,54" и

= 0,38"

матрицу M² = m²Q называют корреляционной матрицей уравненных неизвестных (см. § 22).

Заметим, что есть коэффициенты корреляции между уравненными i-м и j-м неизвестными. Так, коэффициент корреляции между первым и вторым углом

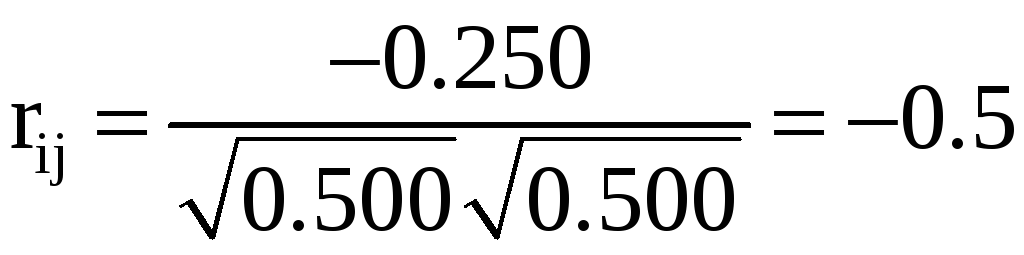
Способ Ганзена вычисления весовых коэффициентов. Рассмотренный выше способ вычисления весовых коэффициентов называют способом дополнительных столбцов. В этом способе вычисляют все величины Q_jj, Однако объем вычислений можно сократить, если воспользоваться свойством симметричности матрицы Q. В самом деле, приняв для простоты k=3, напишем три системы эквивалентных уравнений, соответствующих системе нормальных уравнений (3.43). Будем иметь

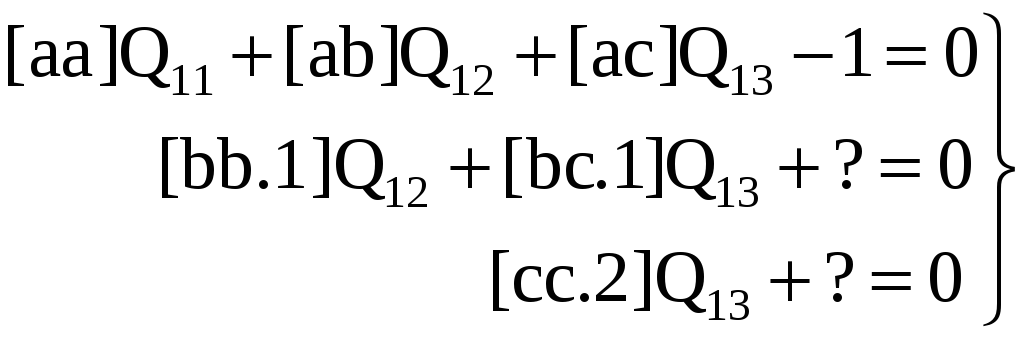(3.44)

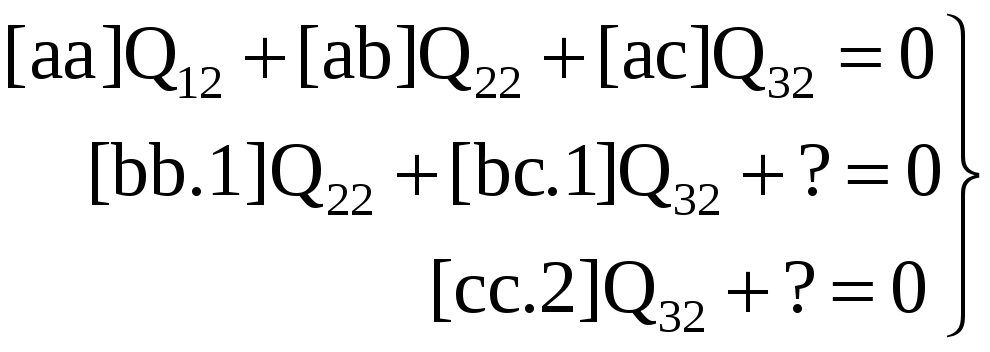(3.45)

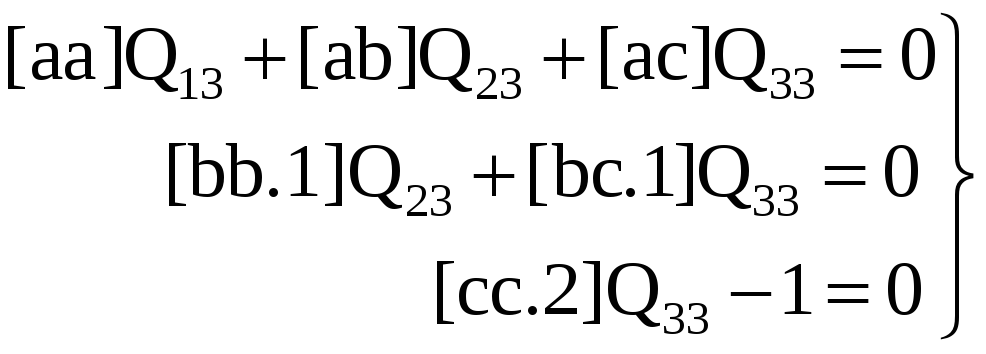(3.46)

Здесь знаком вопроса заменены свободные члены этих уравнений, вычислить которые не придется. Далее из последнего уравнения системы (3.46) сразу находим

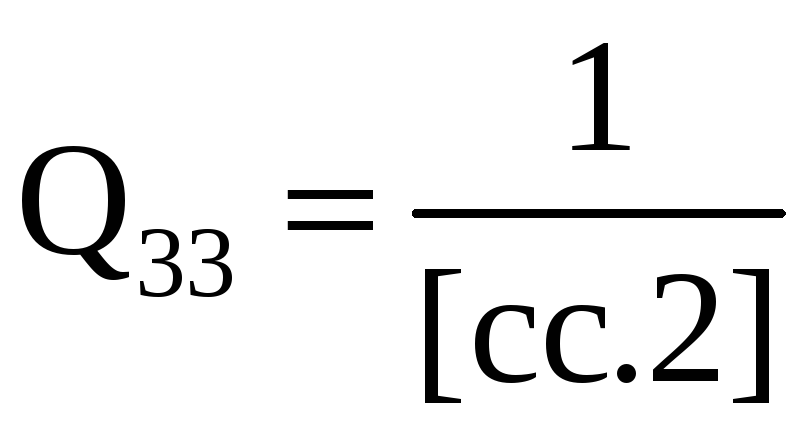(3.46’)

из второго уравнения

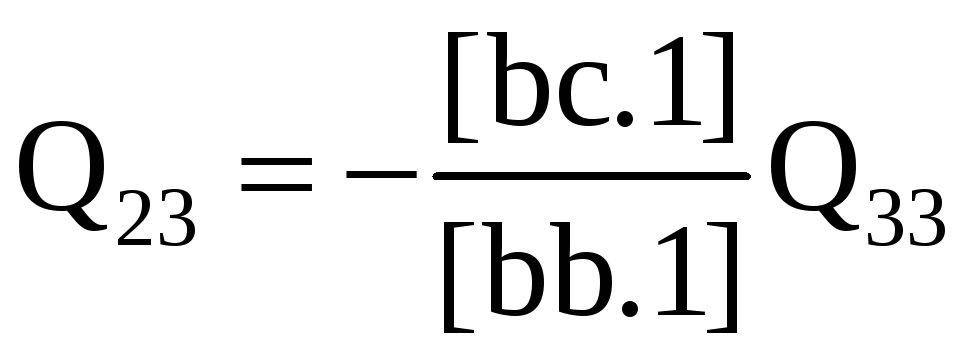
и, наконец,

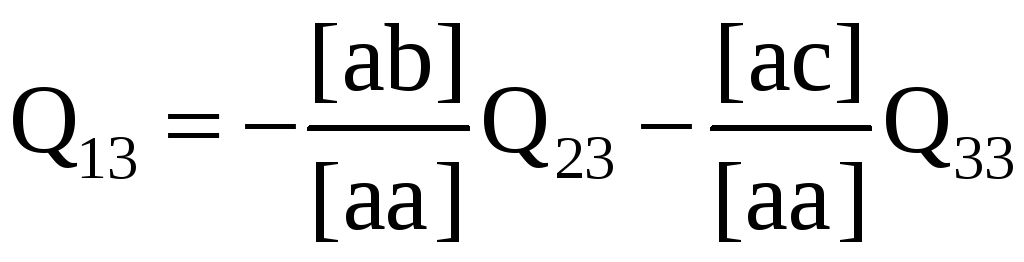
Таким образом, для вычисления столбца

вводить дополнительный столбец свободных членов и не требуется (величина 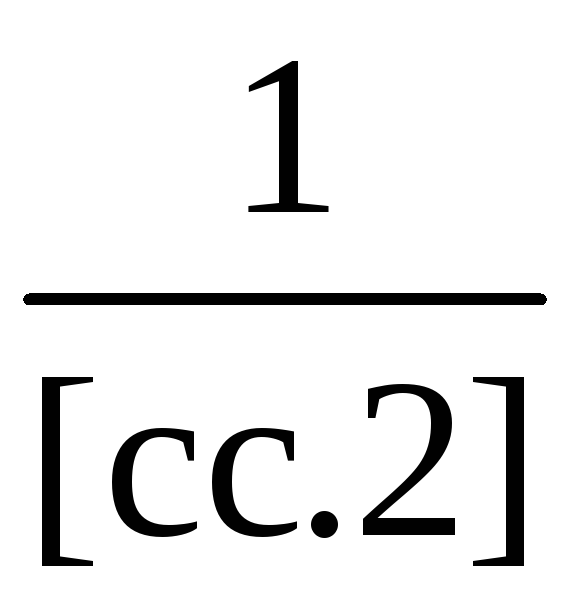уже содержится в схеме Гаусса как вспомогательная величина, остальные же числа элиминационных строк этого столбца равны нулю).

Поскольку Q₃₂ = Q₂₃, то последнее уравнение в системе (3.45) для определения Q₃₂ не потребуется. Приняв в качестве Q₃₂ величину Q₂₃, из второго уравнения (3.45) находим

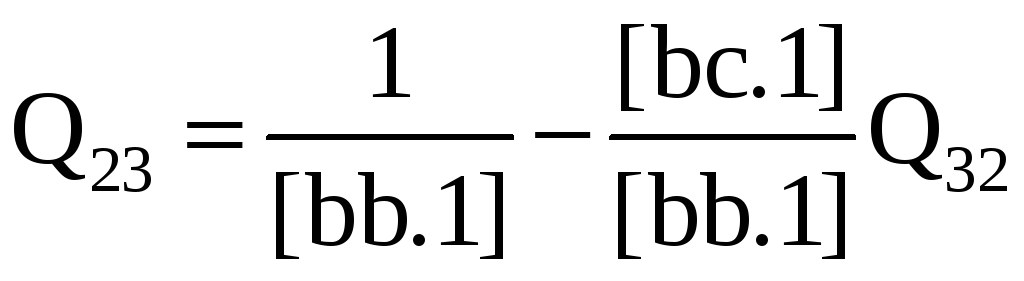
а из первого уравнения

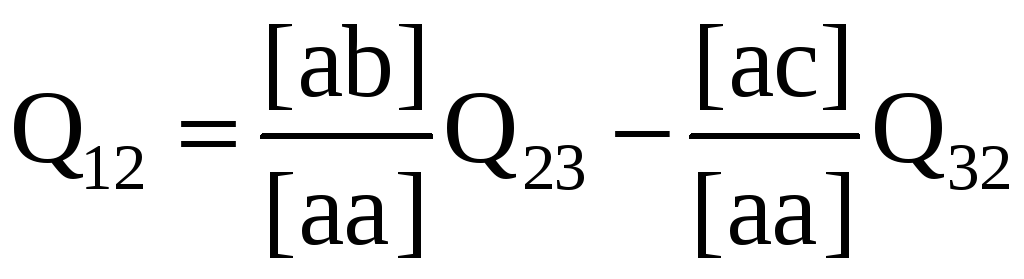
Замечаем, что величина 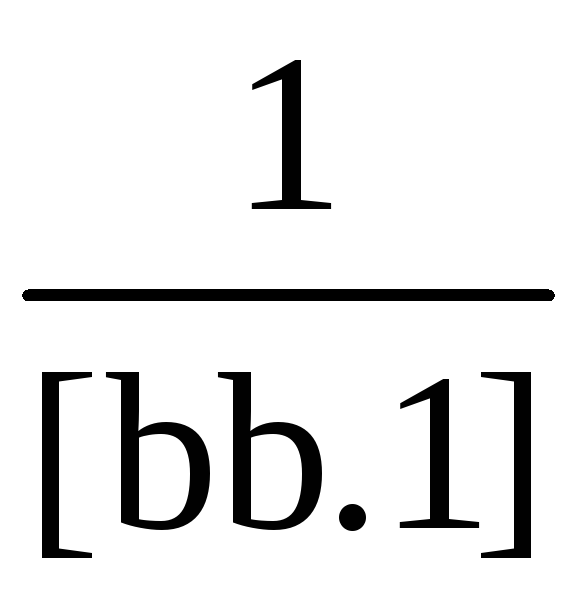уже имеется в схеме Гаусса, а элемент первой элиминационной строки в дополнительном столбце свободных членов равен нулю. Так что и для получения столбца Q₂, как и столбца Q₃, также не нужно вводить дополнительный столбец. Рассуждая аналогичным образом и переходя к системе (3.44), находим

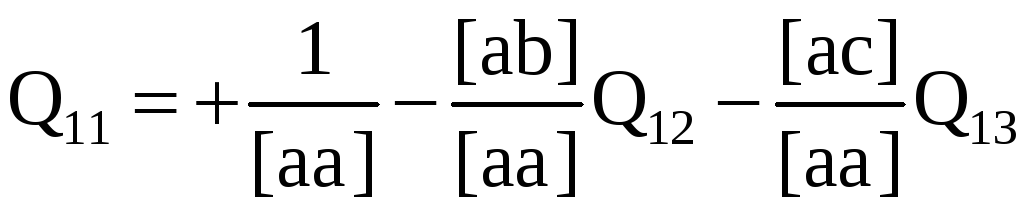
приняв Q_n = Q₂₁, Q_l3 = Q₃₁.

Ясно, что и в этом случае нет необходимости вводить дополнительный столбец свободных членов.

Вычисления целесообразно располагать по следующей схеме (на примере задачи 3.17).

(0,3333)	3,00 (-1,000)	2,00 -0,667	1,00 -0,333
(0,3745)		2,67 (-1,000)	1,33 -0,498
(0,5000) Контроль			2,00 (-1,000)
1,000	0,500	-0,250	0
0,998	-0,250	0,499	-0 ,249	= Q
1,002	0	-0,249	0,500

В ней вычисления начинают с последней строки (в которой размещают элементы столбца Q₃), как описано выше. В дальнейшем все вычисляемые величины заносят в нижнюю часть этой схемы, выделенную жирной ломаной линией. В верхнюю же часть заносят числа из нижней по мере продвижения по строкам вверх. Так, вычислив элементы третьей строки, число -0,249 переносят во вторую строку, а вычислив элементы второй строки, начиная с 0,499, в первую строку переносят элементы -0,250 из второй строки и из третьей. В первой строке вычислений находится лишь элемент Q₁ = 0,500.

Следует, однако, иметь в виду, что при вычислении Q_ij этим способом ошибки, которые могут быть допущены, не обнаруживаются и вся матрица Q может быть получена неверной. Поэтому каждый столбец Q_j начиная с последнего, следует контролировать дополнительно. Необходимые для этого равенства вытекают непосредственно из формулы (3.43) и имеют вид

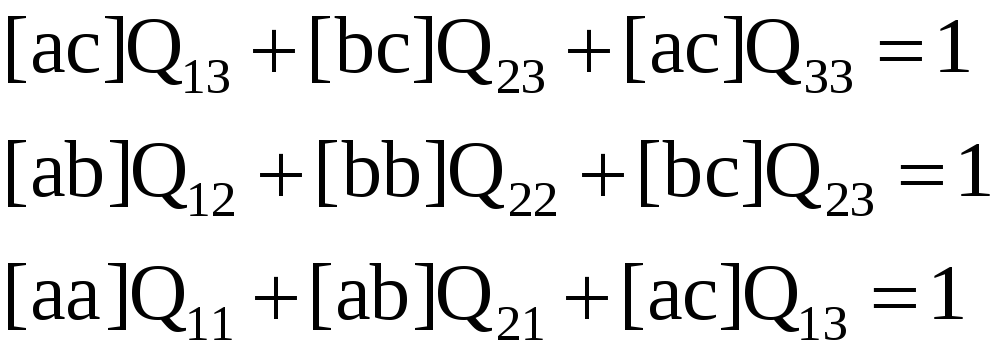
Полученные правые части этих равенств целесообразно записать в специальном столбце «Контроль» (см. схему). Расхождения здесь допустимы до 0,002-0,003 (при вычислении элементов матрицы Q - до 0,001).

Хотя этот способ изложен нами для k = 3, его несложно обобщить и на любое число k. Заметим также, что оба рассмотренных способа применяют для обращения симметричных матриц как вручную, так и на ЭВМ и называют способом Гаусса.

Из формул (3.41) и (3.46') следует сразу, что вес последнего неизвестного р_x3 =[cc.2] или в общем случае

(3.46")

Нетрудно получить также формулу для вычисления веса предпоследнего неизвестного

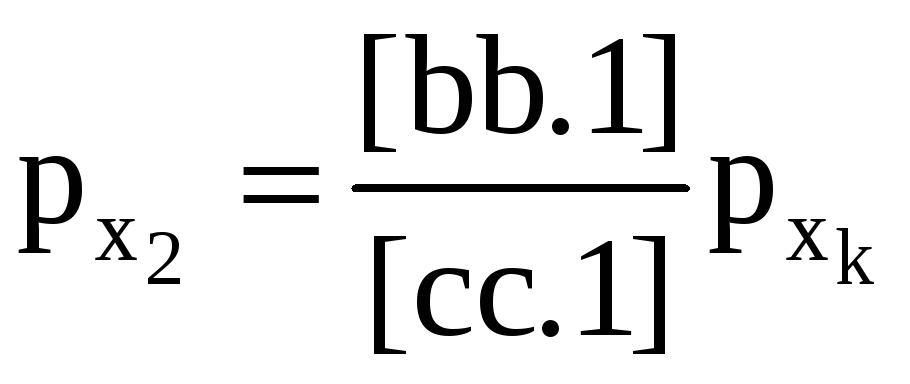(3.47)

или в общем случае

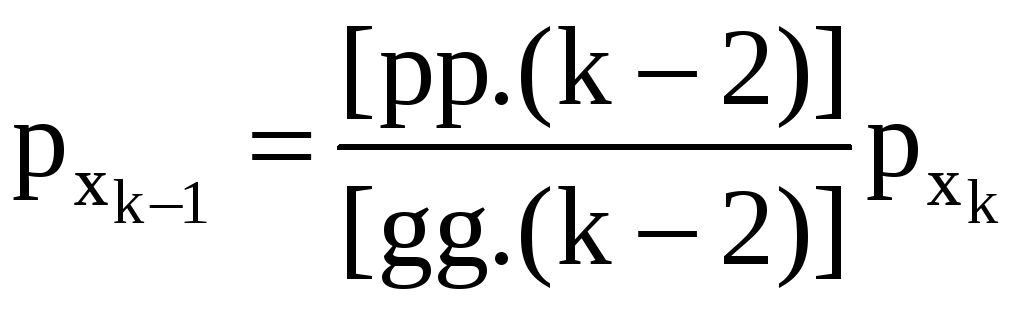(3.48)

Так, в нашем примере р_Х3 = 2,00.

Алгоритмы Гаусса

Поэтому

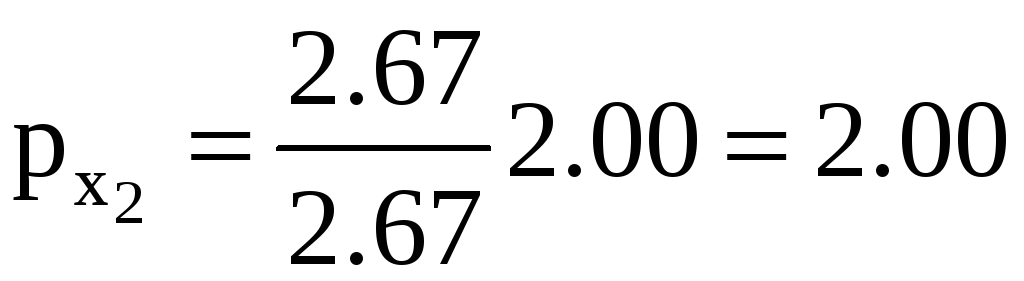
Так как веса и легко вычислить, то последними в геодезической сети обычно нумеруют те пункты, которые предполагают наименее точными из всех (расположенные в самом слабом месте).

3.18. Решить по способу Гаусса, применяя сокращенную схему, одну из следующих систем нормальных уравнений:

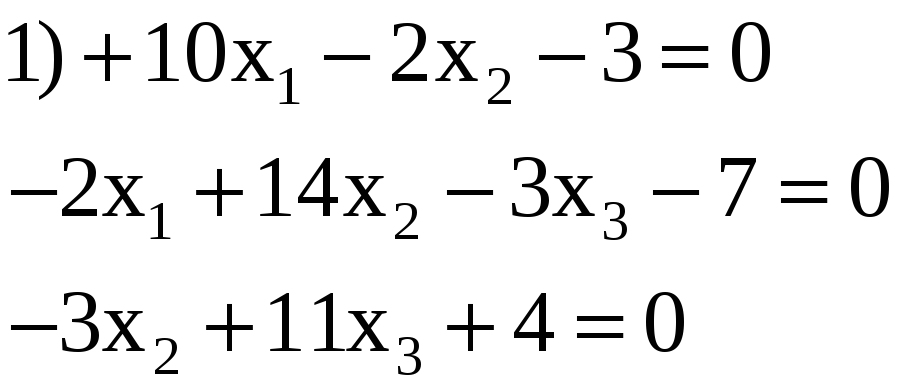
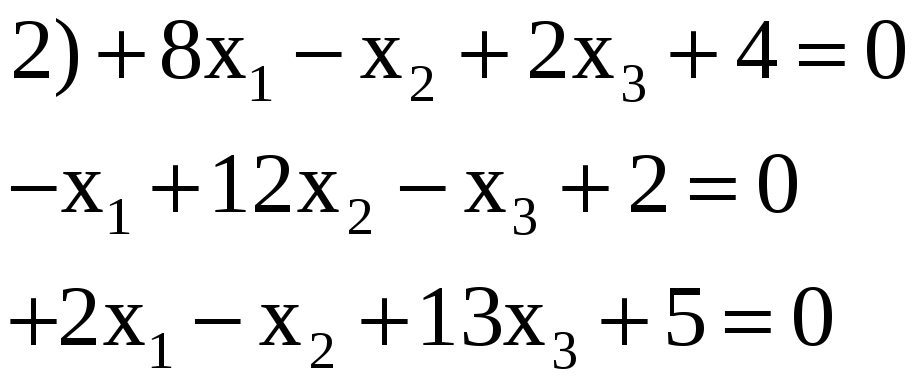
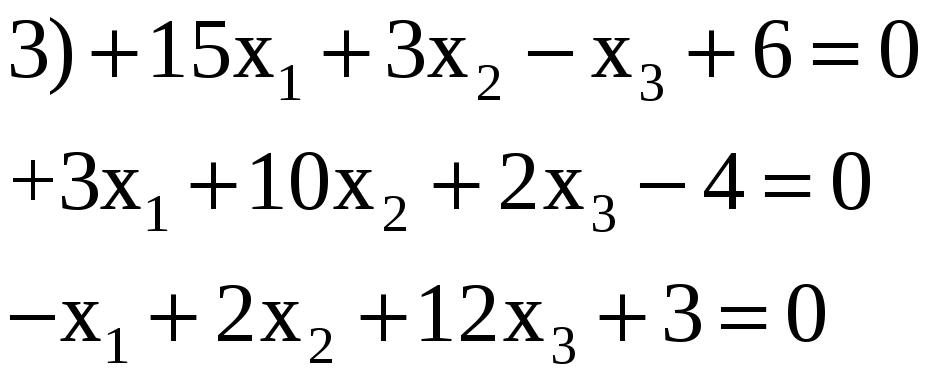
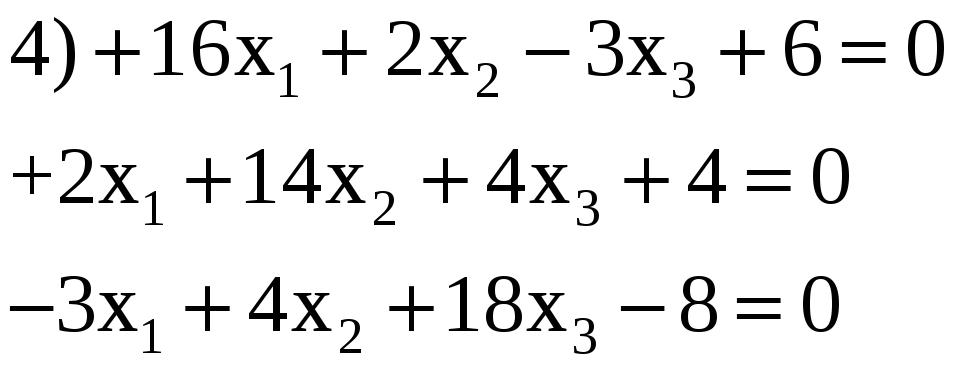
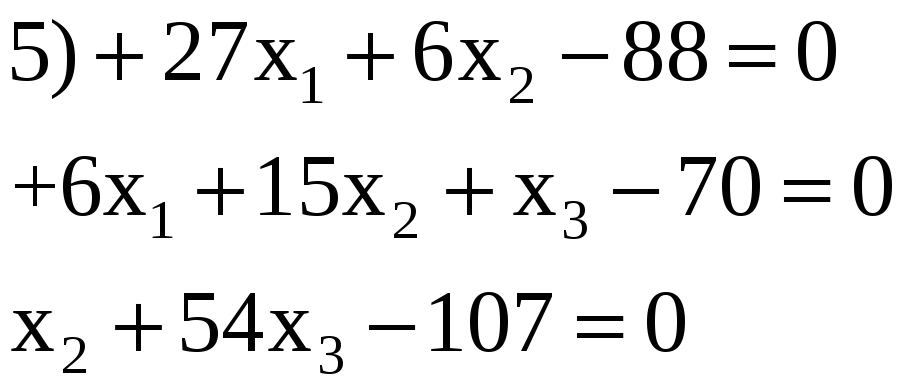
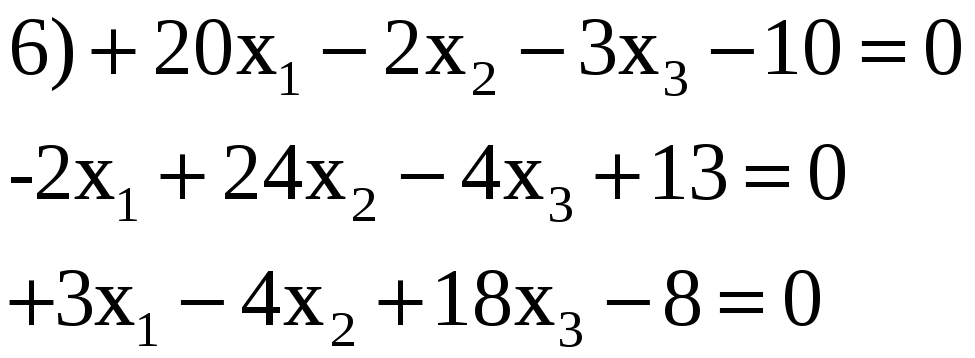
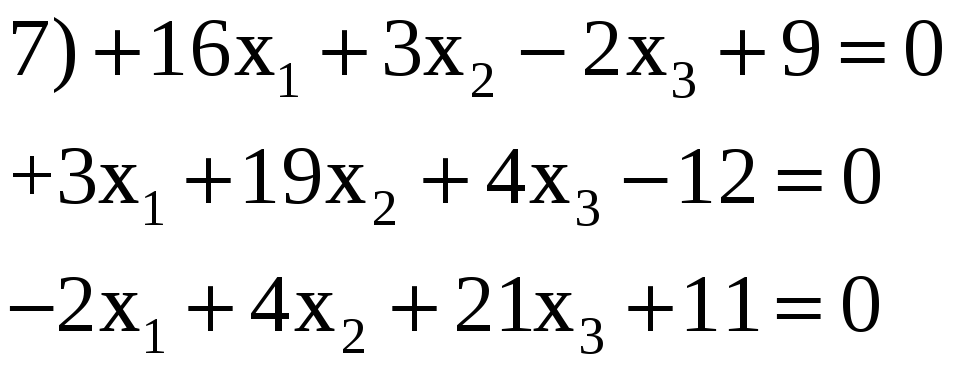
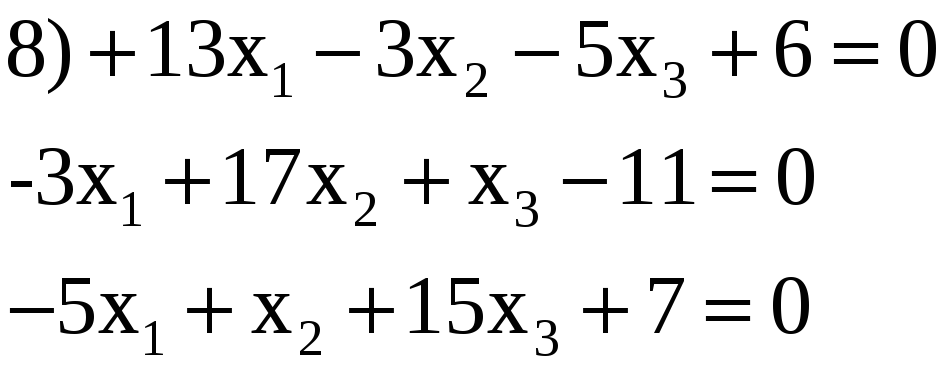
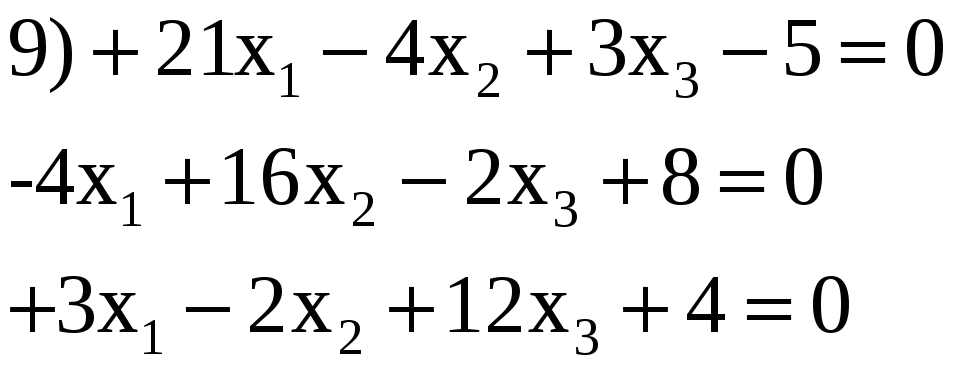
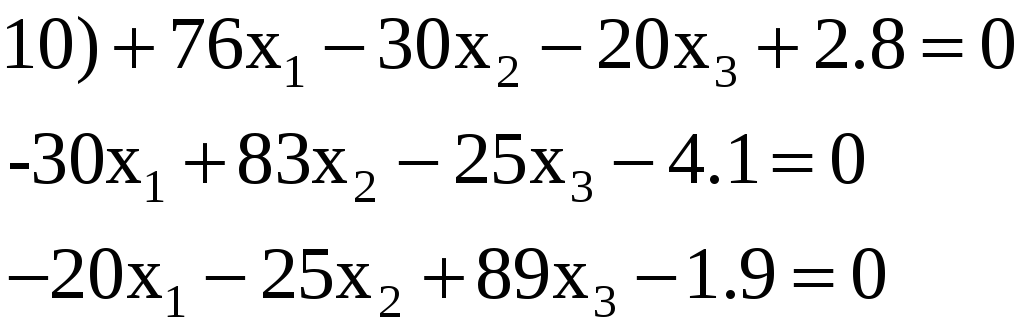
Ответы:

1) 0,402; 0,509; —0,225.

2) —0,408; 0,107; —0,314.

3) —0,557; 0,648; —0,404.

4) 0,356; 0,318; 0,314.

5) 2,468; 3,552; 1,915.

6) 0,413; —0,462; 0,272.

7) —0,834; 0,927; —0,779.

8) —0,559; 0,583; —0,705.

9) 0,209; —0,506; —0,470.

10) —0,013; 0,050; 0,028.

3.19. Обратить по способу Ганзена матрицу коэффициентов одной из систем нормальных уравнений, приведенных в задаче 3.18.

3.20.Является ли нормальной матрица

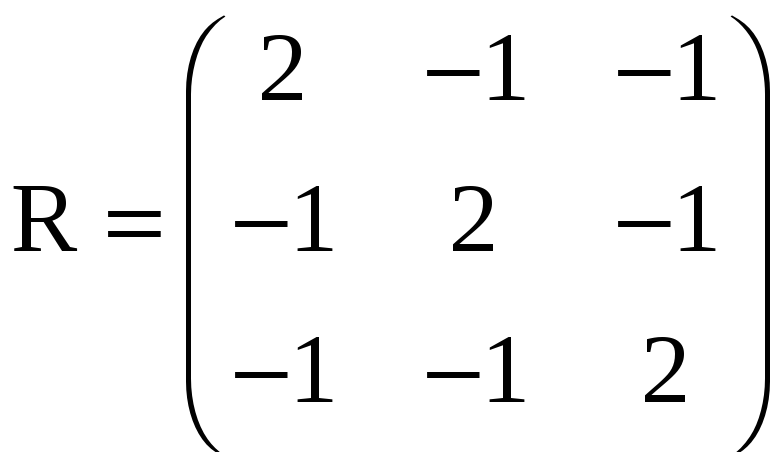
Указание! Вычислить ее определитель согласно формуле (3.28).

Ответ: нет.

3.21. Будет ли являться нормальной матрица R = A^TA, если матрица

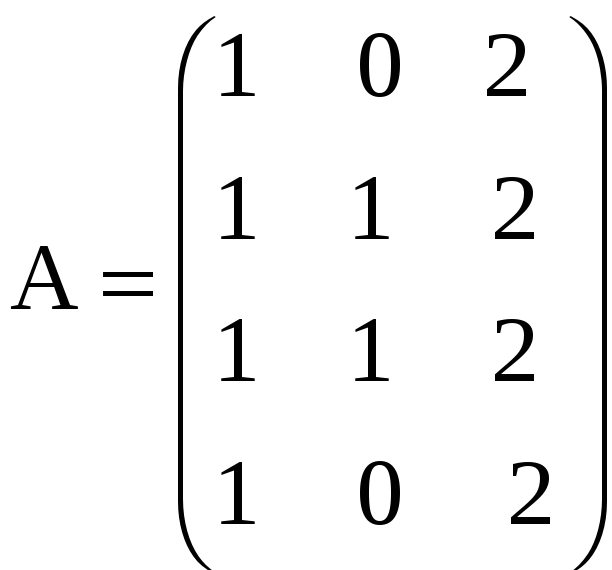
3.22. Составить уравнение поправок, нормальное уравнение и оценить точность уравненного неизвестного в общем виде для случая n-кратного измерения одной и той же величины. Доказать, что x= [х]/n, р_х = n, а также (см. § 21).

3.23. Дана матрица весовых коэффициентов уравненных координат x_Ay_A, x_By_B,

Найти все шесть коэффициентов корреляции между уравненными координатами.

Ответ :