Мат.ожидание

МО- хар-ет центр определения вер-ти СВ . для дискрет. - для непрерывн.

x_i – значение СВ; p_i – вер-сть того, что СВ приняла значение x_i . Сравнивая формулы для дискрет., и непрерывной вел, видим, что элемент вероятности φ(х)dx играет для непрерывн. СВ ту же роль что и вер-сть попадения в точку p_i для дискретной СВ.

СВ-ва: 1) МО постоянной равно самой постоянной М(с)=с. 2) Постоянную можно вынести за знае МО: М(сх)=сМ(х); 3) МО суммы равно сумме МО: М(х+у)=М(х)+М(у); 4) МО произв равно произв МО, только для независимых величин: М(ху)=М(х)*М(у).

Моменты распределения

Явл. наиболее общими числовыми хар-ми. 1) Начальным моментом порядка S явл. МО от СВ в степени S: .

Где x_i - i-тое значение СВ, p_i – вер-ть i-го значения СВ, S – порядок момента

2) Центральным моментом порядка S – назыв МО уклонениыя значения СВ от ее МО в степени S:

3)Абсолютный момент – уклонения берутся по абс.величине:

Дисперсия

Дисперсией назыв. центральный момент 2го порядка. Характеризует рассеивание значения СВ вокруг МО.

-МО квадратов уклонений. D(x)= ; . Также для вычисления используют формулу: Dx=α₂-α₁² . Св-ва: 1) дисперсия постоянной=0: D(c)=0; 2)Постоянную можно выносить за знак дисперсии в квадрате: D(cx)=c²D(x); 3)Дисперсия суммы СВ равна сумме дисперсий для независим СВ: D(x+y)=D(x)+D(y); 4)Дисперсия не линейной ф-ии: F(x)=f(x1, x2...xn). , где

Значение дисперсии выражается в кв.ед , это не удобно, поэтому не используються ср.кв.отклонение, еоторое равно корню из дисперсии:

Кореляц.Зависимость

Функцион.зависимость – каждому значению одной переменной соответствует одно значение другой переменной (Н. у=3х). Вероятностная зависимость – каждому значению одной переменной соотв. распределение значений другой переменной (Н.рост и вес человека). Корреляционная назыв зависимость, когда каждму значению одной переменной соотв. МО другой. Линия соотв. корреляц.зависимости назыв. линией регрессии. Приведенная линия регрессии отражает прямолинейную корреляц.зависимость.Н.если зависимость установлена и выражена формулой то ее можно использовать для организации и обработки результатов измерений. (Н. врямя выхода из дома, время попадания в университет)

Система св

Системой СВ назыв. совокупность СВ, которые для своей хар-ки требуют знания двух или нескольких СВ. (Н.отметки точек теод.хода). Для них также вводятся законы распределения плотность и числовые хар-ки которые буду назыв. совместными. Закон распределения СВ задают в виде ф-ии совместного распределения.

Система 2 СВ. Ф-я совместного распределения системы 2СВ: . Геометрически ф-я совместного распределения равна вероятности попадания в бесконечный квадрат расположенный ниже и левее точки с корд. х,у. Св-ва 1)F(x2, y2)>F(x1, y1) – ф-я не убывающ. 2) Если хотя бы одна из СВ равна -∞, то ф-я распределения =0. F(x;- ∞)=F(-∞;y)=F(-∞;∞)=0. 3) Ф-я распределения от ∞ равна1, F(∞;∞)=1. 4) Если одна из СВ равна + ∞, то ф-я распределения равна ф-ии распределения от второй СВ. F(∞, y)=F₁(y), F(x, ∞)=F₂(x). Плотность: . Для системы 2х СВ также используют числовые хар-ки: смешанный начальный момент порядка s,t: α_s,t=M(x_sY_t), смешанный центральный момент порядка s,t: . Если s или t равны 0, мы получаем начальный момент одной СВ:

Корреляц.момент(допис в интеграле бесконеч)

Центральный смешанный момент 1го порядка и назыв кореляц. Вычисл.:

где Pxy – обозначаеться вер-ть того что СВ Х приняла значение х, а СВ Y приняла значение y

Если между СВ х,у отсутствует зависимость кореляц. Момет равен 0, но из равенства 0 кореляц момента следует лишь то что между СВ х и у отсутствуют корел. зависимость.

Коэффициент корреляции

Неудобства кореляц момента состоит в том, что он содержит единицы СВ. Для того чтобы освободиться от единиц измерения вводят величину которую назыв. коэф.кореляц. Вычисл.: , где k_xy – кореляц.момент, σ_х σ_у – ср.кв.отклонение величины х и у. Св-ва:1) -1≤r≤+1. 2)r=0 (между СВ х и у отсутствует корреляц. зависимость); 3)если коэф корреляц. равен ±1 между СВ х, у существует прямая (если +) или обратная (-) функциональная зависимость.

Уравнение регрессии

Если коэф. кореляц. явл. хар-кой тесноты кореляц. зависимости, то форму связи показывает у-е регрессии.

, ρ_у/х – коэф.регресии. Вычисл. По формуле: ρ_у/х =r*σ_x/σ_y , σ_x,σ_y - ср.кв.отклонения х и у.

Система нескольких СВ (векторы ф-ии)

Несколько СВ представим в виде вектор ф-ии:

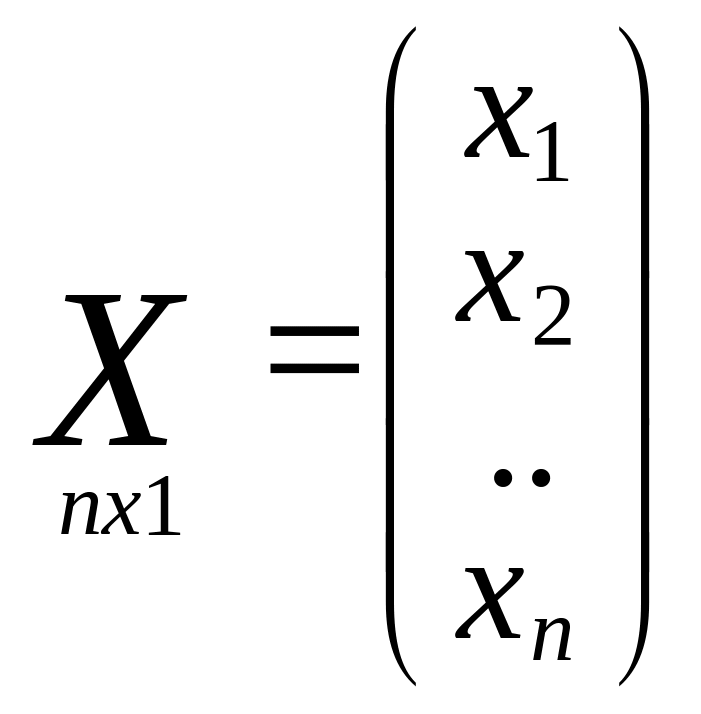
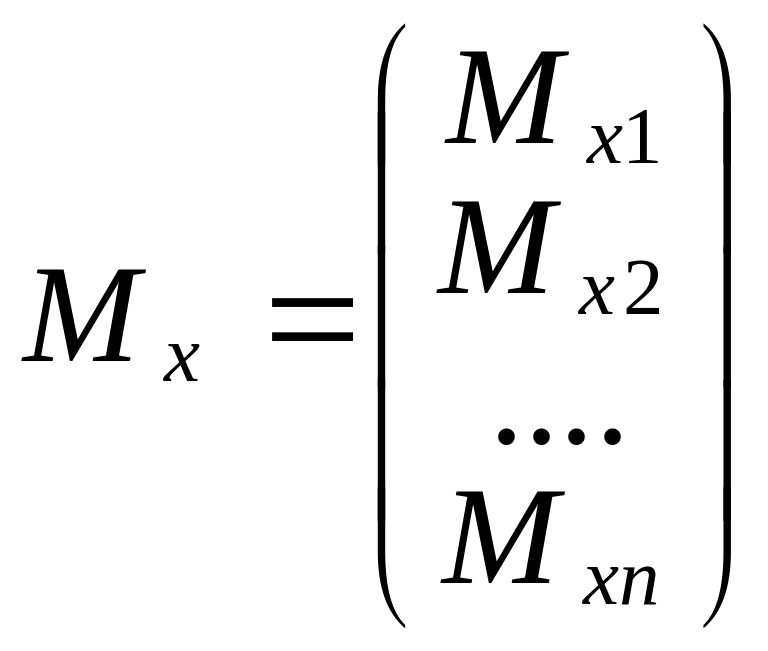
Ф-я совместного распределения для нескольких СВ будет равна:

Плотность совместного распределения:

Обобщенным понятием дисперсии будет матрица равная:

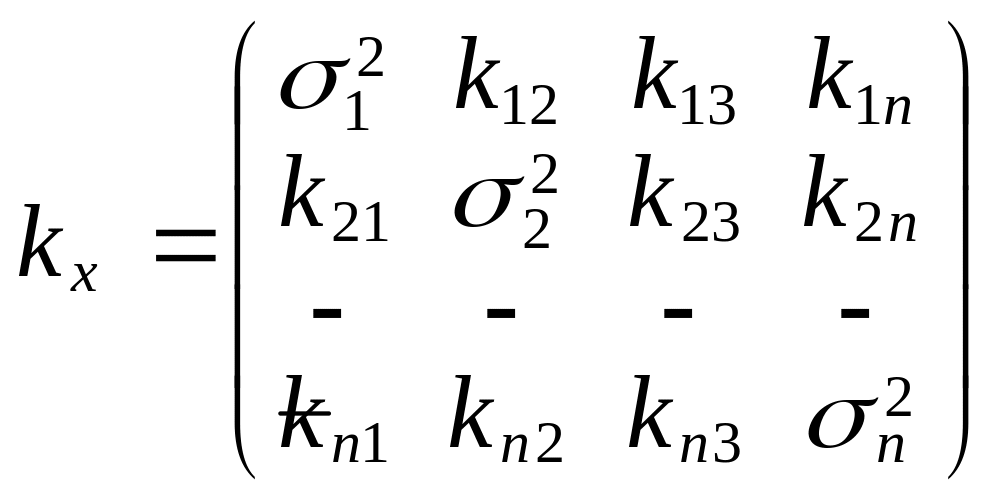
По диагонали в кореляц. матрице стоят дисперсии каждой СВ. Не диагональные элементы это кореляц. моменты между соотв. СВ. Кореляц. матрица симметрична оносительно главной диагонали. Кореляц. моменты иногда назыв ковариации, поэтому матрицу еще иногда назыв ковариационной.

От ковариационной матрицы переходят к нормированной кореляц матрице. В ней по диагонали стоят единицы, а не подиагонали соотв. СВ (коэф.кореляц)

Ф-ии СВ. Обобщающая теорема оценки точности

для некорелированых СВ

для корелированых СВ

Для системы ф-ии:

Обобщенное понятие дисперсии:

, kx – кореляц.матрица СВ х., А – матрица частных производных i-той ф-ии, по j-ой СВ. Данная формула носит название обобщенная теорема оценки точности

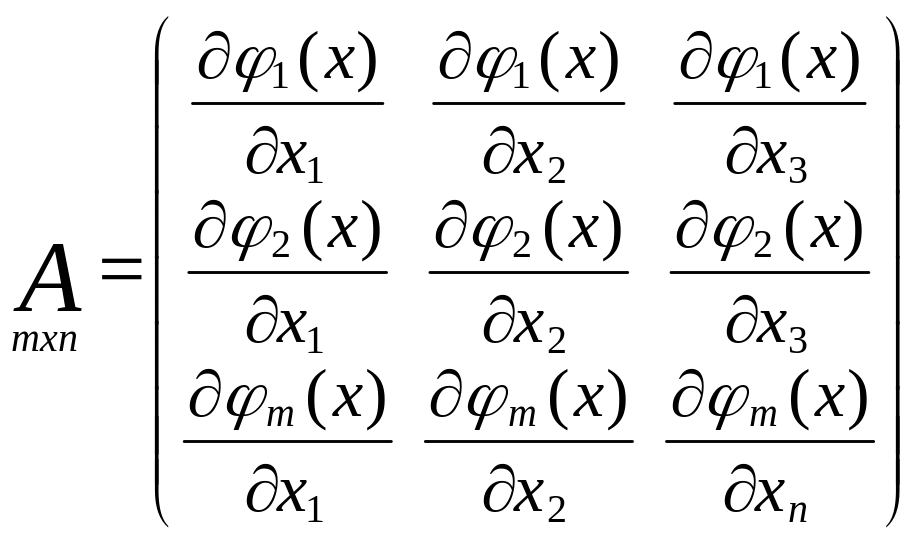
Мат.статистика. Задачи

Мат.статистика – дисциплина, которая занимается разработкой методов сбора, систематизации обработки и анализа статистических данных. Задача 1: определение вида распределения которому подчиняется статистич.данные. Задача2: проверка статистических гипотез. Эта задача возникает когда необходимо проверить соответствие опытных данных каким-то вероятностным суждением, по значениях или поведении исследуемых. Задача3: оценивание параметров распределения( т.е. необходимо таким образом обработать стат.данные, чтобы получить из огранич. числа наблюдений наиболее точные и достоверные результаты, которые были бы как можно ближе теор.знач.)

Выборка и генеральная совокупность

Все возможные знач.СВ назыв. генеральной совокупностью. На практике пользуются ограниченным числом наблюдений для изучения какого-либо явления, эти наблюдения назыв. выборкой из генеральн. совокупности, а отдельные наблюдения назыв. элементами выборки. Элементы выборки должны быть отобраны случайным образом, в этом случае выборку назыв.представительной. Если после наблюдения элементы выборки возвращают в генерал. Совокупность, выборку назыв. повторной ее элементы независимыми. Если не возвращают ее назыв.безповторной, а элементы – зависимыми.

Вариационные и интервальные ряды (рисунки графиков)

При оформлении вариационного ряда подсчитывают число одинаковых значений. Само значение назыв.вариантой, а число значений варианты – частотой. Вариационные ряды оформляются в виде:

вар хi	х1	х2	хk
частота mi	m1	m2	mk
статистич вер.	m1/n	m2/n	mk/n

Вариац.ряды еще назыв.статистич.рядом распределения. Здесь n – общее число наблюдений, mi – число значений варианты xi.

Для построения интервального ряда подсчитывается число интервалов (k=log₂n+1. При этом стараються чтобы число интервалов не превышало 40, а число значений в каждом интервале mi не было меньше 5. Интервалы бывают открытыми и закрытыми.

Многоугольник распределения и гистограмма

Статистич.данные могут быть оформлены в виде графика. Вариационные ряды оформляються в виде многоугольника распределения.

Интервальные ряды в виде гистограмм. Гистограмма представляет собой график состоящий из многоугольников. Основанием которой явл. ширина интервала. Высоты многоугольников пропорциональны статистич. Вероятности попадания в i-й интервал Q. Высота прямой вычисляется по :h=Q/(x_i-x_i-1).

В мат статистике используют стат. аналоги полученых нами ранее величин:
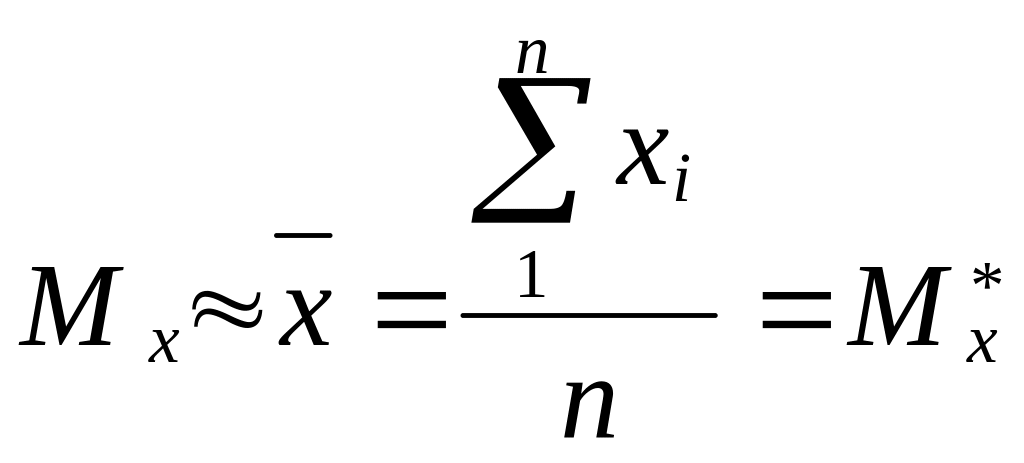
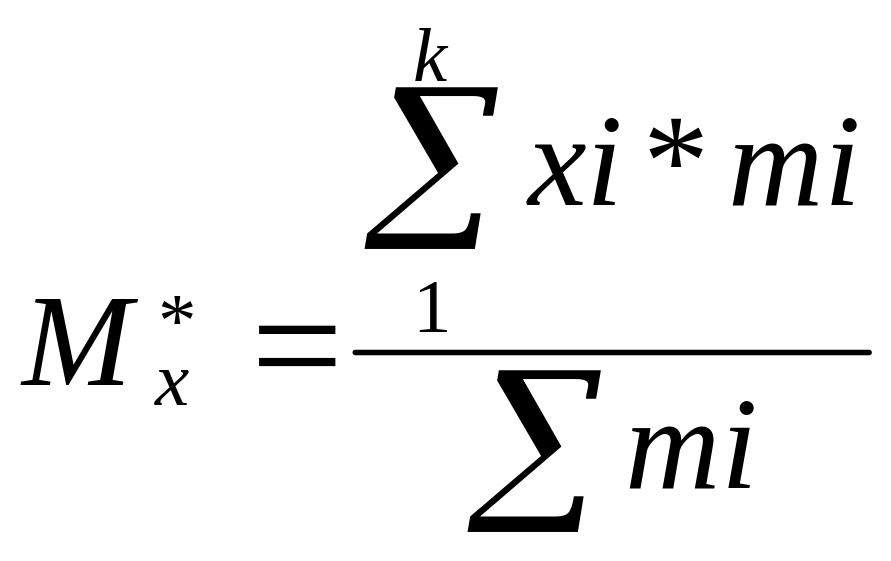
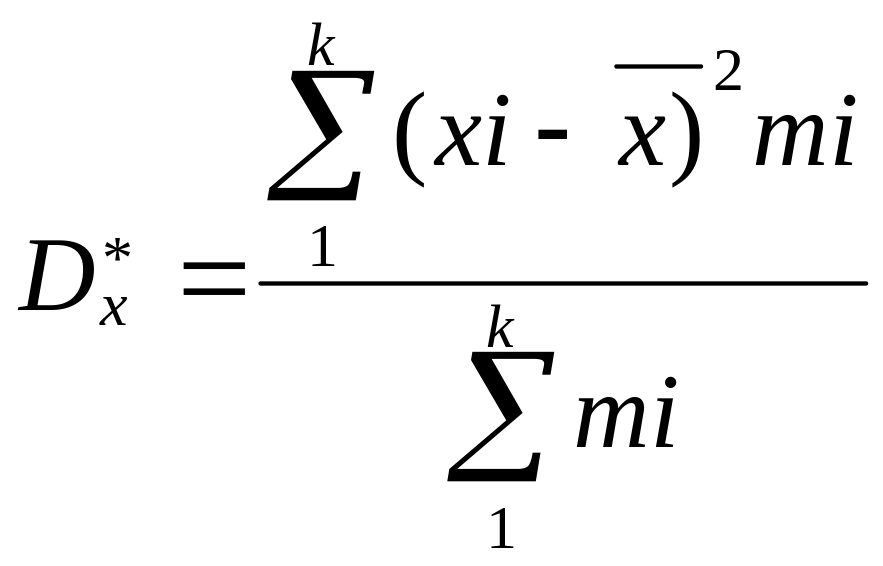